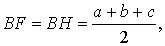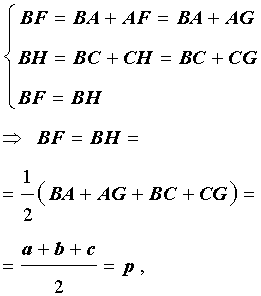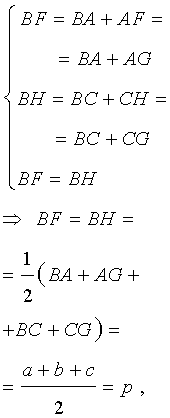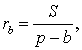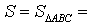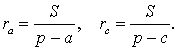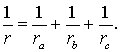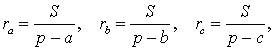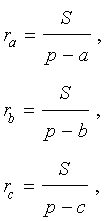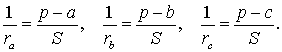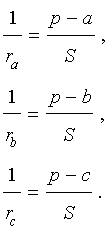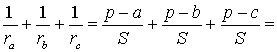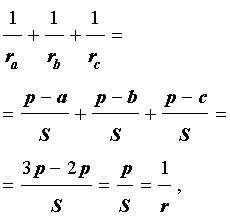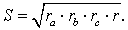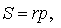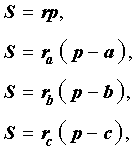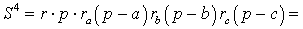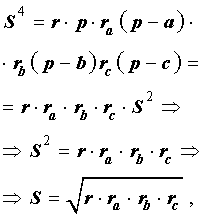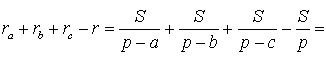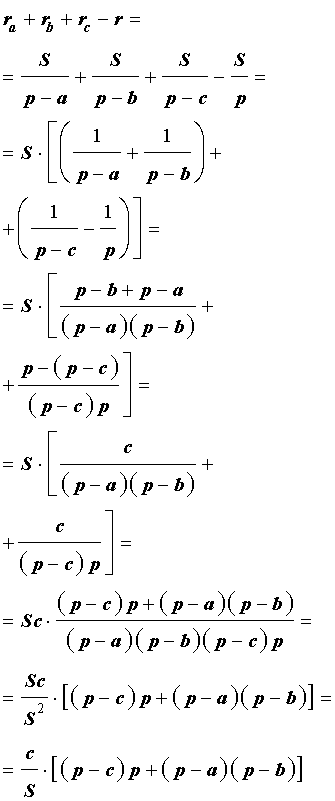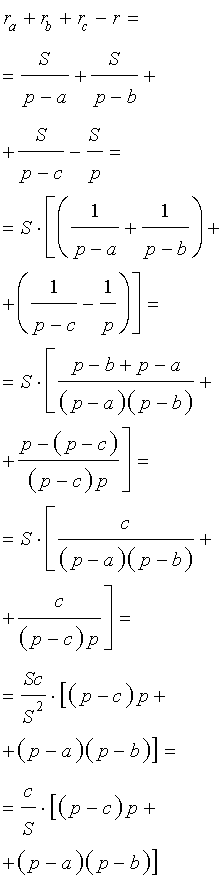Вневписанная окружность формула площади треугольника через радиус вневписанной окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

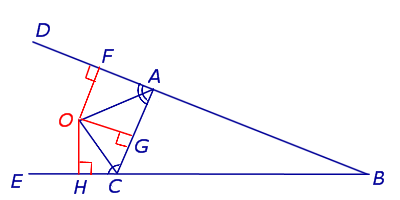
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

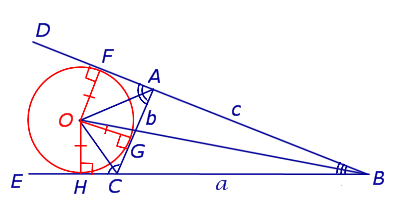
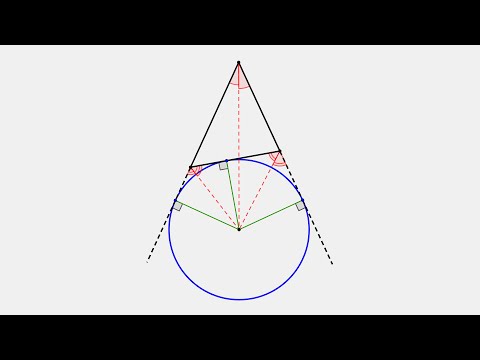
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

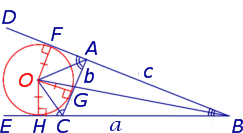
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Видео:✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Как найти площадь треугольника

О чем эта статья:

8 класс, 9 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Радиус вневписанной окружности. Вывод формулы.Скачать

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Видео:Вневписанная окружностьСкачать

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!

Видео:[12] Площадь через радиус вневписанной окружности. Теорема о трилистнике, трезубец, Теорема МансионаСкачать

Общая формула

1. Площадь треугольника через основание и высоту

, где — основание, — высота.

2. Площадь треугольника через две стороны и угол между ними

, где , — стороны, — угол между ними.

3. Площадь треугольника через описанную окружность и стороны

, где , , — стороны, — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны

, где , , — стороны, — радиус вписанной окружности.

Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:

5. Площадь треугольника по стороне и двум прилежащим углам

, где — сторона, и — прилежащие углы.

6. Формула Герона для вычисления площади треугольника

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

, где , , — стороны, — полупериметр, который можно найти по формуле:

Видео:Математика за минуту: Формула радиуса вневписанной окружности в произвольный треугольник.Скачать

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и радиус вписанной окружности

, где — гипотенуза, — радиус вписанной окружности.

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу

, где , — части гипотенузы.

Площадь прямоугольного треугольника по формуле Герона

, где , — катеты, — полупериметр, который можно найти по формуле:

Видео:Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через высоту

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

МАТЕМАТИКА

Рассмотрим произвольный треугольник АВС и проведем биссектрису . Затем продолжим эту биссектрису за точку до пересечения в точке с биссектрисой внешнего угла при вершине В (рис.1). Поскольку точка лежит на биссектрисе угла А, то она равноудалена от прямых АВ и ВС. Следовательно, она равноудалена и от прямых АС и ВС, а значит, лежит на биссектрисе внешнего угла при вершине С.

Продолжение биссектрисы треугольника, проведенной из одной из вершин, пересекается с биссектрисами внешних углов при двух других вершинах в одной точке.

Поскольку точка равноудалена от сторон внешних углов при вершинах В и С, то окружность с центром , касающаяся стороны ВС, касается также и продолжений сторон АВ и АС (рис.2).

Эта окружность называется вневписанной окружностью треугольника АВС. Ясно, что любой треугольник имеет три вневписанных окружности. (рис.3).

Положение центра вневписанной окружности можно охарактеризовать так: это точка пересечения биссектрис внешних углов при вершинах В и С. Можно охарактеризовать его и совершенно иначе, если заметить, что точки , В и С и центр О вписанной в треугольник АВС окружности лежат на одной окружности с диаметром (рис.4), – это следует из того, что углы и прямые.

Можно сказать, таким образом, что точка представляет собой точку пересечения прямой и окружности, описанной около треугольника ВОС.

Принимая во внимание замечание в конце статьи (Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности), из этого можно сделать еще один вывод:

Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, симметричны относительно середины этой стороны.

В самом деле, пусть D – точка пересечения продолжения биссектрисы с описанной около треугольника АВС окружностью (рис.5). Тогда согласно упомянутому замечанию DB = DC = DO. Следовательно, D – центр окружности, описанной около четырехугольника . Проведем из точек O, D и перпендикуляры к стороне ВС и обозначим их основания буквами P, Q и R соответственно (рис.6). Точки P и R являются точками касания вписанной и вневписанной окружностей со стороной ВС, а точка Q – середина этой стороны. Но , значит, и PQ = QR, то есть точки P и R симметричны относительно точки Q.

Точка касания вневписанной окружности со стороной треугольника обладает еще одним замечательным свойством:

Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам.

Можно убедиться в этом самостоятельно, используя рис. 7.

При решении задач, связанных с нахождением площади треугольника, часто полезной бывает следующая формула. Пусть – радиус вневписанной окружности, касающейся стороны треугольника, равной а, р – полупериметр треугольника. Тогда

Обозначим эту формулу (1).

Действительно, если две другие стороны данного треугольника равны b и c (рис. 8), то

Замечание. Выпуклый четырехугольник может не иметь вписанной окружности, но он всегда имеет четыре вневписанные окружности.

Любопытно, что для площади S такого четырехугольника имеет место соотношение, похожее на формулу (1).

В самом деле, пусть стороны данного четырехугольника равны последовательно a, b, c и d; p – его полупериметр, и – радиусы вневписанных окружностей, касающихся сторон, равных а и с. Допустим, что две другие стороны не параллельны (случай параллельных сторон рассмотрите самостоятельно). Продолжим их до пересечения в точке М (рис.9).

Пусть и – точки, в которых продолжения одной из сторон касаются вневписанных окружностей, причем лежит на окружности, вписанной в маленький треугольник. Площадь S четырехугольника равна, очевидно, разности площадей большого и маленького треугольников. Периметр маленького треугольника равен , а периметр большого треугольника равен

Применяя к большому треугольнику формулу (1), а к меньшему – формулу , выражающую его площадь через радиус вписанной окружности и полупериметр, получаем:

Обозначим эту формулу (2)

С другой стороны, из подобия треугольников и ( и – центры вневписанных окружностей) находим . Но отрезок равен полупериметру большого треугольника, то есть .

Поэтому из полученной пропорции можно найти :

Подставляя это выражение в равенство (2) получим:

Спасибо, что поделились статьей в социальных сетях

Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.

📽️ Видео

Вневписанная окружность | Теоремы об окружностях - 3Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Вневписанная окружностьСкачать

✓ Неравенство, которое вынесло почти всех | ЕГЭ-2018. Задание 15. Математика. Профиль | Борис ТрушинСкачать

ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Свойства вневписанной окружности #огэ #егэ #геометрияСкачать

Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Формула радиуса вневписанной окружности в прямоугольный треугольник, касающейся гипотенузы.Скачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

ПЛОЩАДЬ ТРЕУГОЛЬНИКА через радиус вписанной окружностиСкачать

ЕГЭ 2021 Математика. Метод площадей. Теорема Чевы. Вневписанная окружностьСкачать