Виды треугольников по длине сторон (6 видео)

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

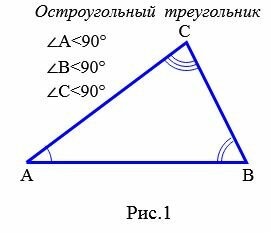
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

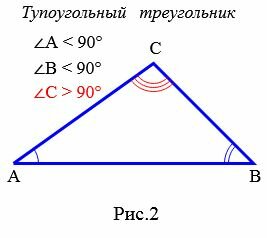Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

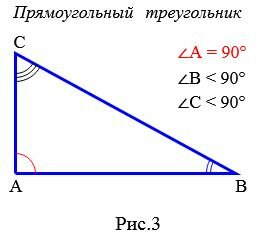Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

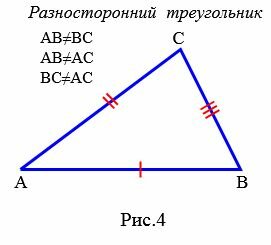
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

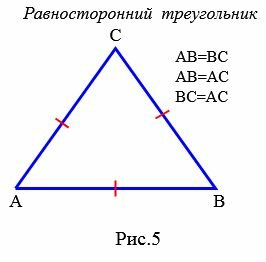
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

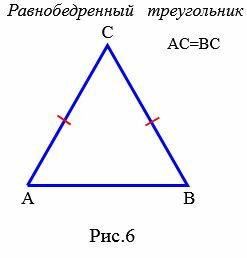В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Содержание

Виды треугольников
Виды треугольников по углам
Виды треугольников по сторонам
Виды треугольников по длине сторон. Периметр треугольника.
🔍 Видео

Видео:Геометрия 7 кл. Треугольники. Определение. Обозначение. Компоненты. Особенности. Виды треугольников.Скачать

Виды треугольников

Треугольники различаются между собой по характеру углов и по характеру сторон.

Видео:Виды треугольниковСкачать

Виды треугольников по углам

Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.

Стороны, образующие прямой угол называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.

Тупоугольный треугольник – это треугольник, у которого один из углов является тупым, то есть больше 90°.

Видео:Виды треугольниковСкачать

Виды треугольников по сторонам

Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.

Равные стороны называются боковыми сторона треугольника, а третья сторона, не равная двум другим, называется его основанием.

Равносторонний треугольник – это треугольник, у которого все три стороны равны, то есть имеют одинаковую длину.

Видео:Виды треугольников по видам угловСкачать

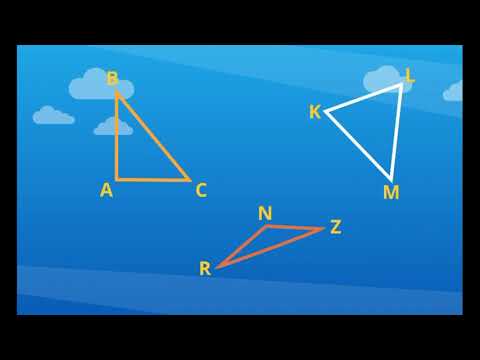
Виды треугольников по длине сторон. Периметр треугольника.

Билет №1

Виды треугольников по длине сторон. Периметр треугольника.

Равнобедренный (равны две стороны), разносторонний (все стороны по величине разные), равносторонний -все стороны равны Периметром треуг называется сумма длин его сторон)

Смежные углы (определение). Теорема о сумме смежных углов.

Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными лучами (т.е. имеют общее начало и дополняют друг друга до прямой).

Сумма смежных углов равна 180°.

Дано: ∠АОВ и ∠ВОС смежные.

Доказать: ∠АОВ + ∠ВОС = 180°

∠АОС = ∠АОВ + ∠ВОС по свойству измерения углов,

∠АОС = 180°, так как является развернутым, ⇒ ∠АОВ + ∠ВОС = 180°

3. Задача по теме «Признаки равенства треугольников».

Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD.

Билет №2

Отрезок (определение). Середина отрезка. Основное свойство расположение точек на прямой.

Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину.
Середина отрезка — это точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка.

из трёх точек на прямой одна и только одна лежит между двумя другими.

Свойства равнобедренного треугольника (доказательство одного из них).

Свойства равнобедренного треугольника:

1. В равнобедренном треугольнике углы при основании равны.

пусть АВС — равнобедренный треуг с основанием АВ. Докажем, что у него А= В.

Тр САВ равен тр СВА по первому признаку равенства треугДействительно, СА=СВ, СВ=СА, угол С= углу С.Из равенства треугольников следует, что угол А= углу В. Теорема доказана.

2 В равнобедренном треуг биссектриса , проведённая к основанию , является медианной и высотой .

Рассмотрим треугольники ACF и BCF (важно правильно их назвать!)

1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))

2) ∠ACF=∠BCF (так как CF — биссектриса по условию).

3) сторона CF — общая.

Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон и углов.

Таким образом, AF=BF, следовательно, CF — медиана.

∠AFC=∠BFC. А так как эти углы — смежные, значит, они прямые: ∠AFC=∠BFC=90º.

Значит, CF — высота.

Что и требовалось доказать.

3. Задача по теме «Окружность и ее элементы».

Найдите длину радиуса окружности, если длина диаметра равна 14,5 см.

Билет № 3

Основные геометрические фигуры на плоскости. Основное свойство принадлежности точек и прямых.

Основными геометрическими фигурами на плоскости являются точка и прямая. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

Построение треугольника по трём сторонам.

Даны три отрезка: a,b иc, равные сторонам искомого треугольника..

В этом случае перед началом построения необходимо убедиться, исполняется ли неравенство треугольника (длина каждого отрезка меньше суммы длин двух остальных отрезков), и эти отрезки могут быть сторонами треугольника.

1. Провести прямую.

2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B.

3. Провести окружность с центром A и радиусом, равным отрезку b.

4. Провести окружность с центром B и радиусом, равным отрезку c.

5. Точка пересечения окружностей является третьей вершиной искомого треугольника.

3. Задача по теме «Вертикальные углы».

Один из вертикальных углов равен 45º. Найдите остальные углы.

Билет № 4

1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение.

2. Теорема о свойстве катета, лежащего против угла в 30º.

Так как сумма острых углов прямоугольного треугольника равна 90º, то∠B=90º-∠A=90º-30º=60º.Построим треугольник ADC, равный треугольнику ABC.В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).Отсюда, ∠BAD=∠CAD+∠CAB=60º.Следовательно, в треугольнике ABD все углы равны:∠BAD=∠D=∠B=60º.Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.BC=DC (по построению), поэтому 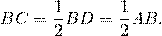Что и требовалось доказать.

3. Задача по теме » Признаки параллельности прямых».

Один из внутренних накрест лежащих углов, образованных при пересечении двух параллельных прямых третьей прямой, равен 50º. Найдите градусные меры остальных углов.

Билет № 5

Билет №6

Билет № 7

Билет № 8

Билет № 9

1. Углы, образованные при пересечении двух прямых секущей. Аксиома параллельности прямых (без доказательства)

При пересечении прямых секущей образуются такие пары углов:

· Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами.

· Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами.

· Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.

Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной

Билет № 10

1. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников (без доказательства).

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

Признак равенства прямоугольных треугольников по двум катетам

Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и гипотенузе

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

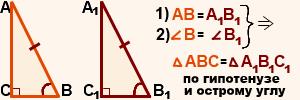
Признак равенства по гипотенузе и острому углу

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и острому углу

Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Билет № 11

Билет № 12

1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

Билет № 13

Билет № 14

Деление отрезка пополам.

	Пусть AB данный отрезок. Описываем окружность радиусом AB с центром в точках A и B. Пусть эти окружности пересекаются в точках С1 и С2.
	Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB.
	Док-во. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 — общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB.

3. Задача по теме » Смежные углы».

Найдите смежные углы, если один из них в два раза больше другого.

Билет № 15

Неравенство треугольника.

Теорема.
Каждая сторона треугольника меньше суммы двух других сторон.

Рассмотрим произвольный треугольник ABC и докажем, что AB

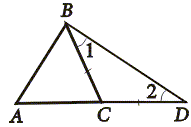В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB

Билет № 16

Билет № 17

Билет № 18

1. Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника (без доказательства)

Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.

1. Сумма острых углов равна 90
2. Катет лежащий против угла 30 равен половине гипотенузы
3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий против него равен 30

Билет № 19

Билет № 20

Теорема.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Доказательство

Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.

3. Задача по теме «Сумма углов треугольника «.

Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.

Билет №1

Виды треугольников по длине сторон. Периметр треугольника.