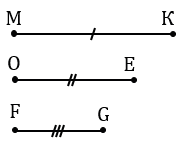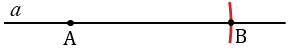Задача:
Построить треугольник по трем его сторонам.
Дано: отрезки МК, ОЕ, FG.
Построить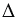 
АВС так, что АВ = МК, ВС = FG, АС = ОЕ.
Решение:
С помощью линейки проводим прямую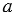 
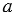
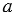
и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой обозначаем В.
Далее, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом).
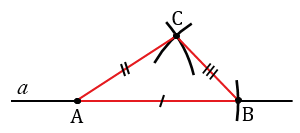
Далее, с помощью циркуля измеряем отрезок FG и строим окружность с центром в точке B радиуса FG (всю окружность строить необязательно, смотри, выделенное зеленым цветом).
Точку пересечения окружностей с центрами в точках А и В радиусами ОЕ и FG соответственно обозначаем С. Соединяем с помощью линейки точки А и В с точкой С. Получаем треугольник АВС, в котором по построению АВ = МК, ВС = FG, АС = ОЕ, следовательно, 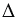АВС — искомый.
Данная задача не всегда имеет решение. Так как для каждого треугольника должно выполняться неравенство треугольника, которое говорит о том, что во всяком треугольнике сумма любых двух сторон больше третьей стороны. Если же какой-нибудь из данных отрезков будет больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.
Поделись с друзьями в социальных сетях:
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать
Треугольник
Рис. 1. Треугольник (общий случай)
Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных). В физике эти отрезки классически называются буквами латинского алфавита ( и т.д.), в отличие от обозначений в геометрии.
Итак, треугольник, у которого все стороны имеют разную длину и ни один из углов не равен , называется произвольным (рис. 1).
В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным.
В случае, если у треугольника все стороны одинаковы, он называется равносторонним.
В случае, если у треугольника один и углов прямой ( ), он называется прямоугольным.
Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:
Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи.
Рис. 2. Треугольник (биссектриса)
Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:
Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3).
Рис. 3. Треугольник (медиана)
Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями:
- через две стороны и угол между ними:
Рис. 4. Треугольник (высота)
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4).
Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями:
- через сторону и площадь треугольника ( )
Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано.
Видео:Произвольный треугольникСкачать
Как начертить равносторонний треугольник
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.
На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.
Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.
При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.
Отметьте точки пересечения окружностей.
Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.
Далее, через центры обеих окружностей нужно провести прямую линию.
Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.
Соедините все три точки между собой.
Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.
🎬 Видео
ГЕОМЕТРИЯ С НУЛЯ. УРОК-5. ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИКСкачать
Построение прямоугольного треугольника по 2 катетамСкачать
Площадь треугольника. Как найти площадь треугольника?Скачать
7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать
Строим треугольник по гипотенузе и катету (Задача 6)Скачать
Произвольный треугольникСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать
Построение высоты в треугольникеСкачать
Построение медианы в треугольникеСкачать
Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать
Виды треугольниковСкачать
Периметр треугольника. Как найти периметр треугольника?Скачать
№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать
Высота, биссектриса, медиана. 7 класс.Скачать
Виды треугольников: остроугольный, прямоугольный ,тупоугольный. Как начертить треугольникСкачать
32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать
Построения с помощью циркуля и линейки. Равнобедренный и равносторонний треугольникиСкачать
