Вес при движении по окружности (7 видео)

Динамика и кинематика движения по окружности: формулы и решение типовой задачи

Умение описывать движение по окружности является важным для проведения расчетов технических характеристик вращающихся валов и шестерен. Этот вид движения также встречается в быту и природе, например вращение планет вокруг Солнца и фигуристов во время выступления на спортивных соревнованиях. В данной статье рассмотрим, как с точки зрения физики можно описать этот вид движения.

Содержание

Динамика вращения
Центростремительная и центробежная силы, ускорение
Кинематические уравнения вращения
Связь линейных и угловых кинематических характеристик
Решение задачи на определение центростремительной силы
Увеличение веса независимо от массы — центробежная сила
Урок по теме «Динамика движения тел по окружности», 10-й класс
Ход урока
📹 Видео

Видео:Физика - движение по окружностиСкачать

Динамика вращения

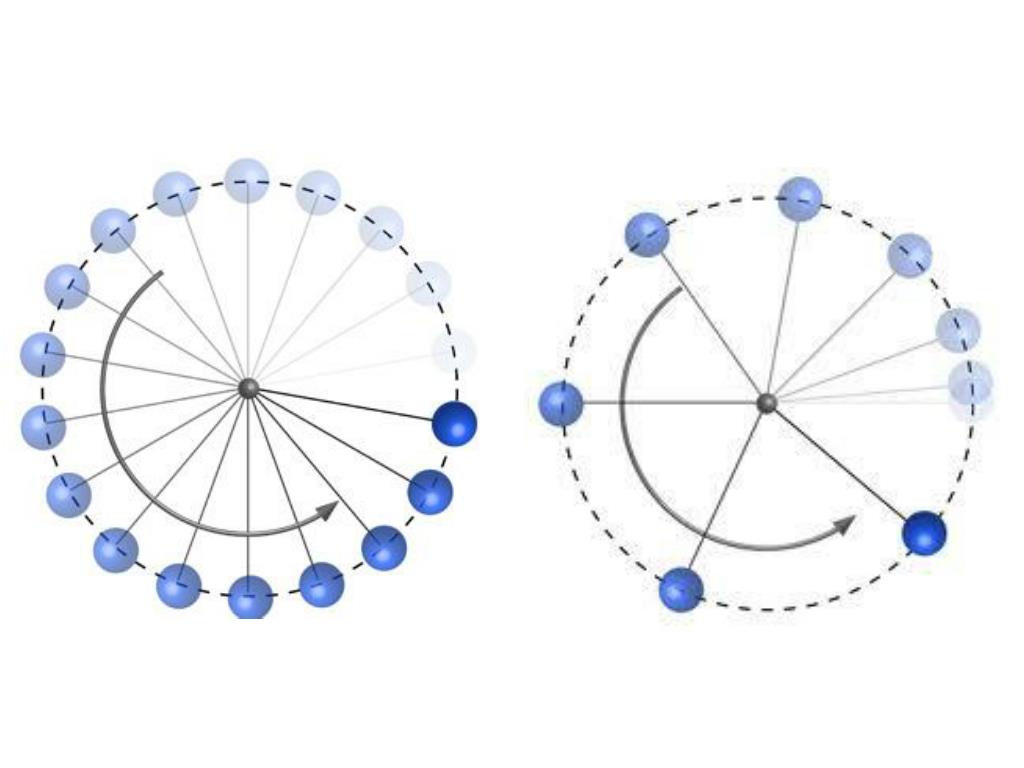
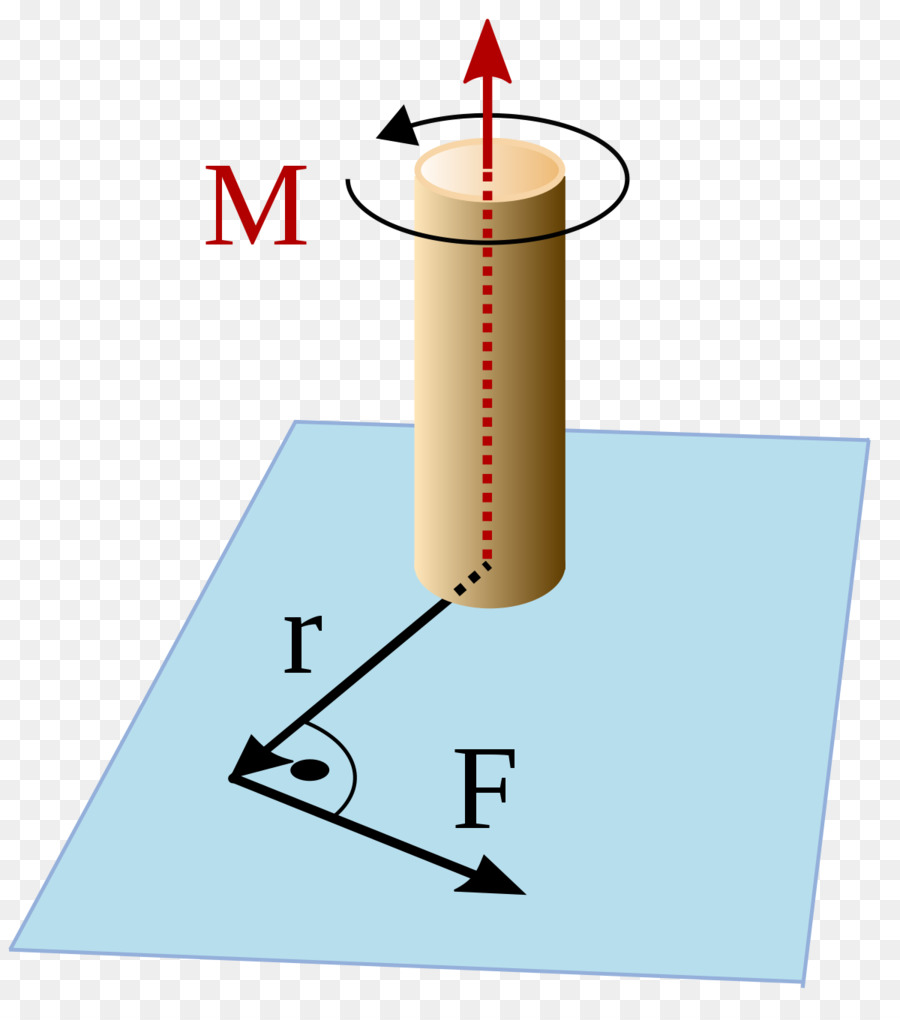
Движение по окружности — это вращение некоторого тела или материальной точки вокруг оси. Чтобы тело начало вращаться, необходимо наличие внешнего момента сил, действующего на рассматриваемую систему. Этот момент определяется по формуле:

Здесь F — сила, d — длина рычага (расстояние между осью и точкой приложения силы). Момент силы является величиной векторной. Приведенная формула используется для расчета модуля M.

Действие момента M отражается на системе в виде появления углового ускорения. То есть система начинает вращаться. Главная формула движения по окружности записывается в виде:

Здесь I — момент инерции, α — ускорение угловое. Обе величины имеют свои аналоги для линейного случая. Если с аналогом величины α все понятно, то для момента инерции I необходимо пояснить. Величина I отражает инерционные свойства вращающейся системы. То есть при вращении она играет такую же роль, как обычная масса тела.

Отметим, что приведенное выражение является аналогом второго закона Ньютона для вращения.

Видео:Вес тела. Невесомость и перегрузки. 10 класс.Скачать

Центростремительная и центробежная силы, ускорение

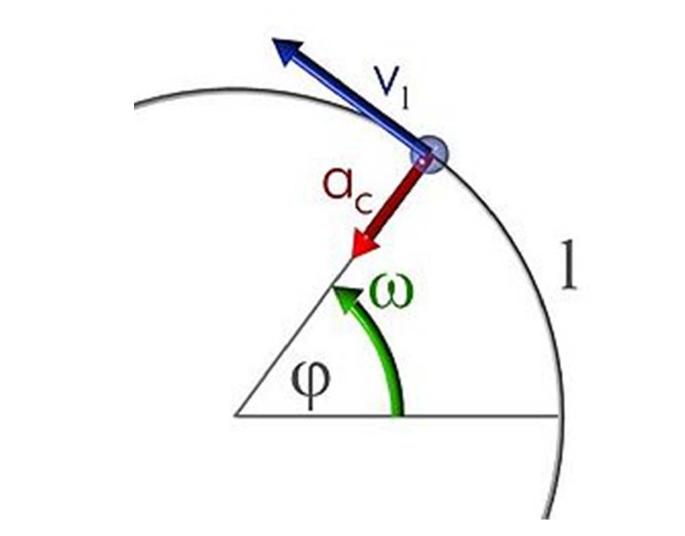
Процесс вращения предполагает наличие некоторой внутренней силы, которая бы обеспечивала криволинейное движение тела. Эта сила называется центростремительной. Согласно названию, она направлена всегда от тела к оси вращения. Поскольку длина рычага d для нее равна нулю, то к возникновению углового ускорения α она не приводит. Тем не менее она изменяет вектор линейной скорости, то есть создает ускорение.

Ускорение при движении по окружности без изменения модуля линейной скорости называется центростремительным. Оно вычисляется по формуле:

Где v — линейная скорость материальной точки, вращающейся на расстоянии r от оси.

Помимо центростремительной, можно часто услышать и о центробежной силе. Последняя стремится вывести тело из круговой траектории на прямолинейную. Причиной ее появления являются инерционные свойства вращающейся системы.

При движении по окружности центростремительная и центробежная силы по модулю равны друг другу, а по направлению они противоположны.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Кинематические уравнения вращения

Движение по окружности, как и по прямой линии, может быть равномерным или происходить с ускорением. В первом случае справедлива формула:

То есть центральный угол θ, на который повернется тело за время t, прямо пропорционален угловой скорости ω. Угол θ выражается в радианах, а скорость ω — в радианах в секунду.

Если действует постоянный внешний момент сил на систему, то движение по окружности происходит с некоторым постоянным ускорением α. В таком случае будет справедливо следующее кинематическое выражение:

Если система сначала вращалась с некоторой скоростью ω_0, а затем стала увеличивать частоту своего вращения с ускорением α, то, начиная с момента времени t, когда появилось ускорение, будет справедлива формула:

Заметим, что это выражение является линейной комбинацией двух предыдущих.

Видео:Вес тела, невесомость. 9 класс.Скачать

Связь линейных и угловых кинематических характеристик

Выше была приведена формула для центростремительного ускорения, записанная через линейную скорость v. Однако эту формулу можно записать также через соответствующую угловую характеристику ω.

Предположим, что вращающееся тело совершило один оборот по окружности за время t. Тогда для линейной и угловой скоростей можно записать:

Откуда видно, что модуль линейной скорости v в r раз больше модуля величины ω, то есть:

Это равенство связывает угловую и линейную скорости. Используя его, можно записать формулу для a_c через ω:

Теперь вычислим в формуле со скоростями производную по времени для левой и правой частей равенства, получим:

Это равенство связывает направленное по касательной к окружности линейное ускорение a и его угловой аналог α.

Нетрудно доказать, что центральный угол поворота θ при движении по окружности связан с длиной ее дуги L, следующим выражением:

Здесь, если θ будет равен 2*pi радиан (полный оборот), мы получим длину окружности L.

Видео:Вес тела (ускорение направлено вверх), перегрузкаСкачать

Решение задачи на определение центростремительной силы

Известно, что к веревке длиной 1 метр привязали камень массой 0,5 кг и стали его вращать с угловой частотой 3 об/с. Необходимо найти силу натяжения веревки F_c.

Сила натяжения F_c является центростремительной. Ее можно вычислить по формуле:

Масса камня m известна. Центростремительное ускорение a_c можно рассчитать из знания угловой скорости ω. С заданной в задаче частотой f величина ω связана выражением:

Тогда центростремительное ускорение будет рассчитываться так:

Искомая сила F_c будет равна:

Если из условия задачи подставить данные в эту формулу, то получится значение силы F_c, приблизительно равное 177,5 Н.

Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Увеличение веса независимо от массы — центробежная сила

Если я свешаю железный кубик, стороны которого равняются 1 см, то я найду, что его вес равняется приблизительно 7,5 г. Если же я захочу получить двойной вес, то я должен взять 2 кубика указанной величины, другими словами, я должен удвоить массу. Увеличивать же вес, не удваивая массы, кажется нам поэтому очень невероятным. Но мы увидим, что в известном смысле можно найти средство к достижении этой цели.
Если мы прикрепим не слишком легкий предмет к нитке и приведем тело в круговое движение, то мы почувствуем как натянулась нитка благодаря подвешенному предмету. Если прикрепить тела различного веса к ниткам одинаковой длины и вертеть их одинаково быстро, то мы заметим, что большая масса будет натягивать нитку больше, чем меньшая масса. Силу, благодаря которой движущееся по кругу тело натягивает нитку, называют центробежной силой.
При одинаковой скорости она пропорциональна массе движущегося тела. Чем меньше радиус круга, тем больше центробежная сила, и чем больше увеличивается скорость движения, тем больше увеличивается сила.
Насколько значительна бывает эта центробежная сила, можно видеть из того, что иногда точильные камни лопаются вследствие быстрого вращения.

Вспомним, как точильный камень отделяет от прижатого куска железа мелкие частички, которые в раскаленном состоянии отбрасываются им в виде искр.

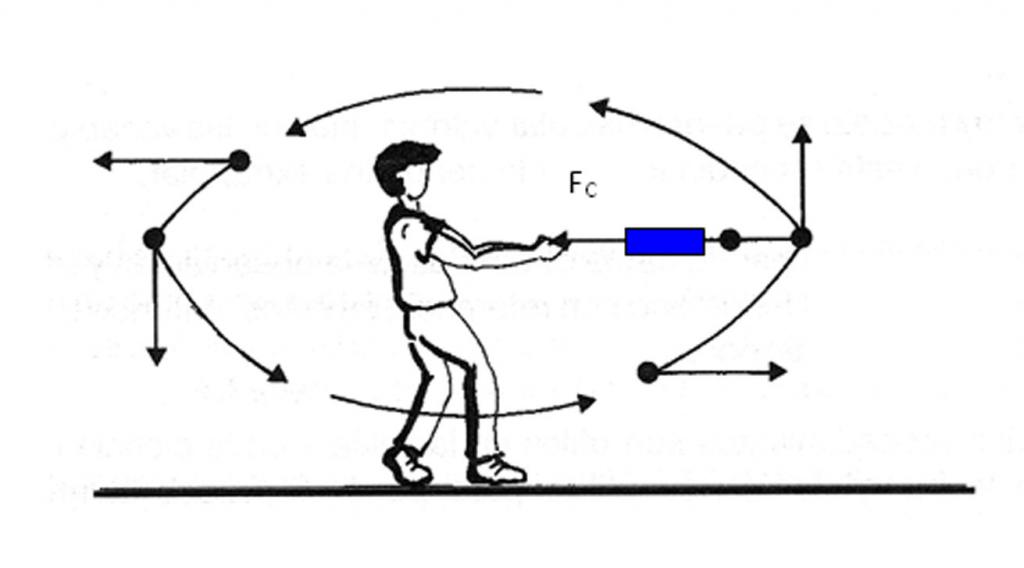
Когда тело во время центробежного движения освобождается от нитки, то оно уже не продолжает своего первоначального кругового движения, но летит прямо по направлению, которое математики называют направлением касательной линии (рис. 31), как известно, это те направления, по которым отрываются частички Н от вращающегося тела.
Из этого видно, что движущееся тело в данный момент стремится к прямолинейному движению (по направлению касательной) и что оно только благодаря двигательной силе нитки совершает кругообразное движение. Вследствие этого, тело (по закону равенства действия и противодействия) производит такое же сильное натяжение по направлению от центра. Вместо шнурка можно употреблять и другие способы, чтобы держать предмет на одинаковом расстоянии от центра. Предмет можно поставить на колеса и заставить его следовать по внутренней стороне кругового пути.

Рис.31. Движение по окружности

Такой случай мы имеем, например, когда велосипедист показывает свое искусство и еще больше того смелость на так называемой «центробежной дороге» (см. рис. 32). Необходимую скорость он приобретает, предварительно спускаясь с крутой наклонной плоскости, которая лежит немного выше, чем тот круг, по которому он желает ехать. Этого достаточно, чтобы велосипед катился по полотну, находящемуся с внутренней стороны кругового пути. При этом велосипедист проезжает высшую точку пути головой вниз и ногами вверх. Одна только центробежная сила прижимает его к опрокинутому сиденью, но он может быть спокоен, если все приспособления безупречны и сам он достаточно владеет своими нервами. Этих примеров пока достаточно, чтобы показать, как при каждом центральном движении возникает центробежная сила.
Так как мы уже несколько раз сказали, что величина этой силы при одинаковом радиусе и скорости зависит от массы тел и так как массу можно определить посредством веса, то можно центробежную силу рассматривать, как один из видов действия веса тела, при котором вес действует не по направлению к центру Земли, как обыкновенно, но по направлению радиусов пути, описываемого движущимся телом. Так как далее центробежная сила увеличивается с увеличением скорости, то, увеличивая скорость движения тела, мы тем самым имеем возможность увеличить действие веса тела, не увеличивая его массы.

Рис. 32. Центробежная дорога

Центробежная сила находит себе очень полезное применение, именно для быстрого разделения тел, которые хотя и сами отделяются друг от друга вследствие различного веса, но значительно медленнее. Таким путем химик отделяет кристаллы и осадки от растворов, в которых они образуются; таким же образом в молочном хозяйстве освобождают и отделяют сливки от тяжелой, водянистой части молока. Разница в удельном весе сливок и водянистой части молока не очень велика: отношение весов равно приблизительно 9:10. Если поэтому оставить молоко стоять, то нужно много часов, пока мельчайшие капельки жира, рассеянные в молоке, частью соберутся сверху в виде сливок.
Предположим, например, что в известном количестве молока находится 9 г сливок, тогда вес вытесненной сливками водянистой части будет 10 г и «выталкивающая сила», т. е. причина поднятия сливок, равна 1 г. Если бы сделать обе части в 1000 раз тяжелее, так, чтобы сливки весили 9 кг, а вытесненная часть молока 10 кг, то «выталкивающая сила» была бы равна 1 килограмму, эта задача осуществлена в центробежном сепараторе.
Простая форма сепаратора, пригодная для лабораторных целей, представлена на рис.33. Рама с 6-10 плечами вращается горизонтально с большой скоростью при помощи особого приспособления, не изображенного на рисунке. На конце каждого плеча находится вращающееся кольцо. В эти кольца вставляются трубки, содержащие вещества, которые надо «центрифугировать». Чтобы не было колебаний прибора, друг против друга должны находиться одинаковые количества жидкости. При вращении этого аппарата под действием центробежной силы трубки отклоняются от своего первоначального положения А кнаружи. Когда они приходят в положение В, где образуют с первоначальным направлением угол в 45° и оказываются, таким образом, посредине между вертикальным и горизонтальным положениями, то сила тяжести, действующая по вертикальному направлению, равна по величине горизонтально действующей центробежной силе. Таким образом, всякий грамм массы внутри трубки, кроме своего веса в 1 г, которому он обязан силе тяжести, еще, так сказать, приобретает 1 г «горизонтального веса» благодаря действию центробежной силы. Центробежная сила пропорциональна квадрату скорости. Таким образом, если машина вращает трубки вдвое быстрее, то развивается вчетверо большая центробежная сила; каждый грамм массы приобретает теперь 4 г горизонтального веса, при удесятеренной скорости каждый грамм приобретает 100 г горизонтального веса и т.д.
Таким путем небольшая первоначальная разница в весе двух тел в такой трубке обусловливает при достаточно быстром вращении прибора весьма значительную разницу в центробежном весе тел, и более тяжелое скоро собирается на наружном конце трубки, т. е. на дне ее. В машинах, основанных на этом принципе и отличающихся от нашего прибора лишь отдельными деталями, ежедневно центрифугируются большие количества молока. Водянистая часть молока гонится при этом во внешние части сепаратора, между тем как более легкие сливки собираются вблизи середины.

Рис. 33, Центрифуга

Подобным же приемом пользуются в больших прачечных, чтобы быстро удалить воду из мокрого белья. На пасеках таким способом извлекают мед из ячеек пчелиных сот, не разрушая этих последних, как это было прежде, когда их разрезали и раздавливали.

Видео:Вес телаСкачать

Урок по теме «Динамика движения тел по окружности», 10-й класс

Разделы: Физика

Класс: 10

“Науку все глубже постигнуть стремись,
Познанием вечного жаждой томись.
Лишь первых познаний блеснет тебе свет,
Узнаешь: предела для знания нет.”

Фирдоуси (персидский и таджикский поэт, 940-1030 гг.)

Цель урока: изучение метода решения задач на определение веса тела, движущегося по окружности в вертикальной плоскости.

Задачи урока:

систематизировать знания по теме: “Вес тела”;
повторить метод решения задач на определение веса тела, движущегося с ускорением по вертикали;
научить решать задачи на определение веса тела, движущегося по окружности;
составить алгоритм решения задач на определение веса тела, движущегося по окружности.

Видео:Центростремительное ускорение. 9 класс.Скачать

Ход урока

I. Актуализация знаний

Тест на повторение домашнего задания. Ученик выполняет задания теста, обменивается с соседом по парте. В ходе взаимопроверки учащиеся проверяют друг друга и выставляют отметку.

Бланк для заполнения

№ вопроса	1	2	3	4	5
Ответ

Тест на тему “Вес тела”

Вес тела — это …
А. Сила, с которой Земля притягивает к себе тело.
Б. Сила, с которой опора или подвес действуют на тело.
В. Сила, с которой вследствие притяжения к земле, тело действует на опору или подвес.
На нити висит шарик массой 200 г. Выберите правильное утверждение.
А. Вес шарика равен 0,2 Н.
Б. Сила тяжести, действующая на шарик, равна 2 Н.
В. Если нить перерезать, то вес шарика будет равен силе тяжести, действующей на тело.
На полу неподвижного лифта, лежит груз массой 3 кг. Выберите правильное утверждение.
А. Если лифт начнет двигаться с ускорением вниз, то вес груза будет равен силе тяжести.
Б. Если лифт начнет двигаться с ускорением вниз, то вес груза будет меньше 30 Н.
В. Если лифт начнет двигаться с ускорением вниз, то вес груза будет больше 30 Н.
Космическая ракета при старте с поверхности Земли движется вверх с ускорением. Вес летчика массой 80 кг будет:
А. Меньше 800 Н.
Б. Равен 800 Н.
В. Больше 800 Н.
Тело брошено вертикально вверх. В каком из нижеперечисленных случаев тело находится в состоянии невесомости?
А. Только при движении вверх.
Б. Только при движении вниз.
В. Все время полета.

№ вопроса	1	2	3	4	5
Ответ	В	Б	Б	В	В

II. Объяснение нового материала

Движение по окружности весьма разнообразно. Весь спектр задач для данного вида движения можно условно поделить на два типа:

движение тел по окружности в вертикальной плоскости (например, движение автомобиля по выпуклому (вогнутому) мосту; вращение тела на веревке; самолет выполняет “ мертвую петлю” и др.)
движение тел по окружности в горизонтальной плоскости (например, движение ИСЗ; движение транспорта на поворотах; конический маятник и др.)

Под действием двух сил, направленных вдоль одной прямой, тело может двигаться не только по прямой, но и по окружности. Рассмотрим движение тела по окружности под действием силы тяжести и силы упругости.

III. Решение задач

Задача №1. Автомобиль массой 5 т движется по выпуклому мосту со скоростью 36 км/ч.
С какой силой автомобиль давит на середину моста, если радиус кривизны моста составляет 50 м? С какой минимальной скоростью должен двигаться автомобиль, чтобы он не действовал на мост в верхней точке?

Полеты самолетов связаны с фамилией легендарного летчика Петра Николаевича Нестерова.

Сообщение учащегося: Выдающийся летчик Петр Нестеров вошел в историю авиации как довольно яркая фигура. Он основоположник фигурного летания (высшего пилотажа), первый летчик, который доказал возможность осуществлять на самолете маневры в воздухе, в том числе как автор петли, которую назвали его именем.

Выпускник Михайловского артиллерийского училища и Петербургской офицерской воздухоплавательной школы. Военный летчик. Погиб в воздушном бою, впервые применив таран.

“Не для забавы иль задора,
А вас мне нужно убедить,
Что в воздухе везде опора.
Одного хочу лишь я,
Свою петлю осуществляя,
Чтобы “мертвая петля”
Была бы в воздухе “живая”. (П.Н.Нестеров)

Задача №2. (Выполните у доски и в тетрадях)
Самолет делает “мертвую петлю” радиусом 100 м и движется на ней со скоростью
288 км/ч. С какой силой летчик массой 80 кг будет давить на сиденье самолета в нижней точке петли? Какую перегрузку испытывает летчик в этой точке?

IV. Составление алгоритма решения задачи на динамику движения тела по окружности.

Прочитайте условие задачи и кратко запишите условие задачи.
Выделите взаимодействующие тела.
Выполните рисунок, изобразив на нём взаимодействующие тела, покажите с помощью векторов силы, действующие на тело, и ускорение.
Запишите уравнение второго закона Ньютона в векторной форме.
Выберите вертикальную ось, направленную вверх или вниз.
Запишите уравнение второго закона Ньютона в проекциях на выбранную координатную ось.
Запишите формулу для вычисления центростремительного ускорения.
Решите в общем виде полученную систему уравнений относительно силы реакции опоры.
Используя третий закон Ньютона, запишите выражение для веса тела.

Выразите, если нужно, неизвестную величину.
Проверьте правильность решения задачи в общем виде путём операций с наименованиями величин, входящих в формулы.
Подставьте числовые данные в СИ в решение общего вида и произведите вычисления.
Оцените полученный результат решения.

V. Самостоятельное решение задач в парах.

Вариант 1

Вариант 2Базовый уровень

Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит на сиденье при прохождении им среднего положения со скоростью 6 м/с?

2. Ведерко с водой равномерно вращают в вертикальной плоскости на веревке длиной 0,5 м. С какой наименьшей скоростью нужно его вращать, чтобы при прохождении через верхнюю точку вода не вылилась из ведра?Базовый уровень

1. Автомобиль массой 1500 кг движется по вогнутому мосту, радиус кривизны которого 75 м., со скоростью 15 м/с. Определите вес автомобиля в средней точке моста.

2. С какой скоростью должен лететь самолет в верхней точке “мертвой петли”, чтобы летчик был невесомым, если радиус петли 360 м?

VI. Домашнее задание

§15, решите задачи:

№1. Груз, подвешенный на нити длиной 1 м, раскачивается. Каков вес груза в нижней точке его траектории? Масса груза 1 кг, а его скорость в нижней точке 2 м/с.

№2. В нижней точке “мертвой петли” летчик давит на сиденье кресла с силой 7,1кН. Масса летчика 80 кг, радиус петли 250 м. Определите скорость самолета.

№3. Самолет выходит из пикирования, двигаясь в вертикальной плоскости по дуге окружности радиусом 1 км. Какова скорость самолета в нижней точке траектории, если летчик испытывал пятикратную перегрузку?

Спасибо за работу.

Рефлексия урока

На отдельном листке ответьте на вопросы: 1. Как ты понял тему урока? 2. Оцени свою работу на уроке..