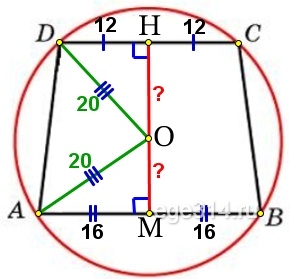
Основания равнобедренной трапеции 32 24 центр окружности (5 видео)

Основания равнобедренной трапеции 32 24 центр окружности

Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.

Найдите высоту трапеции.

Высота трапеции KH = KO + OH, где KO и OH — высоты равнобедренных треугольников DOC и AOB. По теореме Пифагора:

Тогда

Если бы большее основание трапеции лежало выше центра окружности (то есть оба основания располагались по одну сторону от центра окружности) длина высоты равнялась бы не сумме, а разности найденных отрезков. Решая данную задачу необходимо принимать во внимание рисунок, данный в условии.

Хорошо, что было дано примечание насчет оснований по одну сторону и возможного решения в виде разности двух полученных высот. С большим уважением отношусь к вашему сайту, но все же слишком часто (сейчас сходу примеров привести не могу, но по ощущениям) в геометрических задачах рисунок отражает суть задачи крайне приблизительно, но решение все же бывает однозначным. Мне кажется, было бы правильнее такого рода задачи с неединственным ответом в первой части не давать. Помню, что были годы, кода неединственность конфигурации была особой фишкой геометрической задачи С4, но здесь не тот случай.

Согласны с вами.

Задание не наше, а разработчиков ФИПИ, поэтому и обращаем внимание учащихся на спорный момент.

Содержание

Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Основания равнобедренной трапеции равны 32 и 24?
В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?
Основания равнобедренной трапеции равны 72 и 30?
В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?
В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80 , причем центр окружности лежит внутри трапеции?
Около трапеции описана окружность, центр которой лежит внутри трапеции ; Высота трапеции = 27 ; Основания = 48 и 30 ; Найти радиус окружности?
Около трапеции с высотой 8 описана окружность, центр которой лежит внутри трапеции?
В равнобедренной трапеции длины оснований равны 14 см и 40 см, а длина высоты — 9 см?
Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований?
В окружность вписана равнобедренная трапеция с основаниями 14 и 40?
В равнобедренной трапеции длины оснований равны 6 см и 4 см, а длина высоты — 4 см?
📹 Видео

Видео:Где центр окружности? ТрапецияСкачать

Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Через центр окружности О проведём высоту НМ, она делит основания равнобедренной трапеции пополам:

DH = DC/2 = 24/2 = 12
АМ = АВ/2 = 32/2 = 16

Проведём радиусы DO и АО, получаем два прямоугольных треугольника ΔDHO и ΔAMO, найдём в них по теореме Пифагора катеты HO и МО соответственно:

Найдём высоту трапеции НМ:

НМ = НО + МО = 16 + 12 = 28

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Основания равнобедренной трапеции равны 32 и 24?

Геометрия | 5 — 9 классы

Основания равнобедренной трапеции равны 32 и 24.

Радиус описанной окружности равен 20.

Центр окружности лежит внутри трапеции.

Найдите высоту трапеции.

1) OD = OB = OC = OD = 20⇒ΔBOC — равнобед.

Поводим высоту — медиану OK, BK = KC = $frac$ BC = 24 : 2 = 12⇒Δ BKO прямоугольный⇒OK² = OB² — BK² = 400 — 144 = √256 = 16

2)OD = OB = OC = OD = 20⇒ΔAOD — равнобед.

Проводим высоту — медиану OH, AH = HD = 32 : 2 = 16 ⇒ΔAOH прямоугольный OH² = OA² — AH² = 400 — 256 = √144 = 12

3) kh — высота 16 + 12 = 28.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции.

Найдите высоту этой трапеции.

Видео:Задача 6 №27439 ЕГЭ по математике. Урок 51Скачать

Основания равнобедренной трапеции равны 72 и 30?

Основания равнобедренной трапеции равны 72 и 30.

Радиус описанной окружности равен 39.

Найдите высоту трапеции.

Видео:ОГЭ Задание 24 Площадь трапецииСкачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?

Найдите высоту этой трапеции.

Видео:ОГЭ Задание 24 Площадь описанной трапецииСкачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80 , причем центр окружности лежит внутри трапеции?

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80 , причем центр окружности лежит внутри трапеции.

Найдите высоту этой трапеции.

Видео:Основания равнобедренной трапеции равны 3 и 17 ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Около трапеции описана окружность, центр которой лежит внутри трапеции ; Высота трапеции = 27 ; Основания = 48 и 30 ; Найти радиус окружности?

Около трапеции описана окружность, центр которой лежит внутри трапеции ; Высота трапеции = 27 ; Основания = 48 и 30 ; Найти радиус окружности.

И если не затруднит, то с объяснениями, пожалуйста).

Видео:ОГЭ Задание 24 Описанная равнобедренная трапецияСкачать

Около трапеции с высотой 8 описана окружность, центр которой лежит внутри трапеции?

Около трапеции с высотой 8 описана окружность, центр которой лежит внутри трапеции.

Большее основание трапеции видно из центра окружности под углом 110 * , а меньшее под углом 70 * .

Найдите плорщадь трапеции.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

В равнобедренной трапеции длины оснований равны 14 см и 40 см, а длина высоты — 9 см?

В равнобедренной трапеции длины оснований равны 14 см и 40 см, а длина высоты — 9 см.

Найдите радиус окружности, описанной около этой трапеции.

Известно, что центр окружности лежит внутри трапеции.

Видео:Геометрия Площадь равнобедренной трапеции, описанной около круга равна 32√3 см2. Определить боковуюСкачать

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований?

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований.

Найдите периметр трапеции, если один из ее углов равен 60.

Видео:ОКРУЖНОСТИ 1 ЧАСТИ В ЕГЭ И ОГЭ 2024 | МАТЕМАТИКА | МИХАИЛ ОЗИНГЕНСкачать

В окружность вписана равнобедренная трапеция с основаниями 14 и 40?

В окружность вписана равнобедренная трапеция с основаниями 14 и 40.

Центр окружности лежит в трапеции.

Высота трапеции равна 9.

Найдите радиус окружности.

Видео:ОГЭ Задание 24 Площадь трапецииСкачать

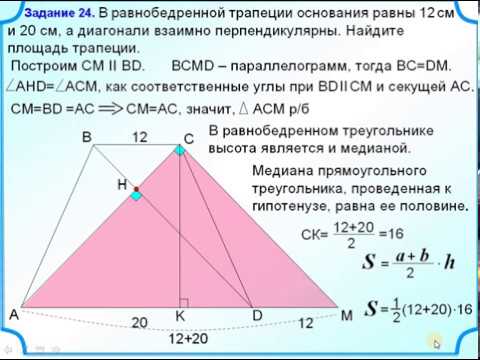
В равнобедренной трапеции длины оснований равны 6 см и 4 см, а длина высоты — 4 см?

В равнобедренной трапеции длины оснований равны 6 см и 4 см, а длина высоты — 4 см.

Найдите радиус окружности, описанной около этой трапеции.

Известно, что центр окружности лежит внутри трапеции.

На этой странице находится ответ на вопрос Основания равнобедренной трапеции равны 32 и 24?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Так как угол CDK = 45 и угол СКД равен 90, то по теореме о сумме углов угол КСД равен 45, поэтому треугольник СКД равнобедренный и стороны СК и КД равны QA = CK = КД = 6 как отрезки, заключенные между параллельными прямыми QAKC — прямоугольник, поэто..

BRS = CBE CBE = (180 — 50) : 2 = 65° BRS = 65°.

Свойство треугольника если напротив стороны есть угол = 30° = половине гипотенузы 18 / 2 = 9см — ac.

АС = АВ * 2 = 17 * 2 = 34 АВ = АС — 10 = 34 — 10 = 24 Р(АВС) = 17 + 34 + 24 = 75 см.

1) a ^ 2 = 15 ^ 2 — 9 ^ 2 = 144a = 12.

№1 угол 1 = 138. Сумма углов параллелограмма = 360 градусов , противоположные углы равны по св — ву параллелограмма. Значит, угол 2 = 138, угол 3 = 42, угол 4 = 42.

S = 3х4х2 + 3х5х2 + 4х5х2 = 24 + 30 + 40 = 94 см2 — площадь поверхности.

Расстояние от M до вершины D — длина отрезка, соединяющего точки М и D / По данному условию задача может быть решена, если отрезокМА перпендикулярен плоскости прямоугольника. Тогда МА перпендикулярна любой прямой, лежащей в плоскости АВСD. Из прямо..

Гр — градусы соот — соответственно уг — угол сумма углов у треугольника равно 180 гр соот уг В = 180 — (30 + 75) = 75гр соот треугольник равнобедренный потому что углы при основании равны и значит что б = с = 4. 5 ну дальше уже не в курсе как.

Точки A bc el расположены как лучь поэтому они расположены на одной плоскости.