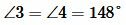Вертикальные треугольники в геометрии (2 видео)

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

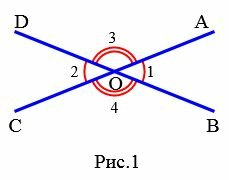На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Содержание

Свойства вертикальных углов
Задачи и решения
Треугольник. Формулы определения и свойства треугольников.
Определение треугольника
Классификация треугольников
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
2.Теорема синусов.
3. Теорема косинусов.
4. Теорема о проекциях
Медианы треугольника
Свойства медиан треугольника:
Формулы медиан треугольника
Вертикальные треугольники в геометрии
Виды углов. Измерение углов
Смежные и вертикальные углы
Свойства смежных и вертикальных углов
Углы при пересечении двух прямых секущей
🎥 Видео

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

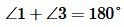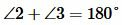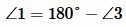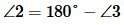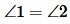
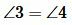
Следовательно . Аналогично доказывается, что .

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

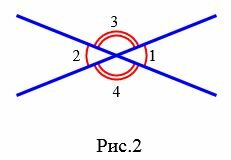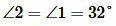
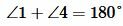
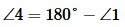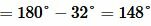Решение. Так как углы 1 и 2 вертикальны, то . Углы 1 и 4 смежные. Следовательно . Тогда

Углы 3 и 4 вертикальные. Тогда

Ответ. .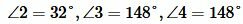

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

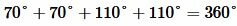Ответ. .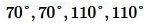

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Видео:Вертикальные углы. 7 класс.Скачать

Определение треугольника

Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.

Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Видео:Признаки равенства треугольников. 7 класс.Скачать

Свойства треугольника

1.Свойства углов и сторон треугольника.

Сумма всех углов треугольника равна 180°:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	=	sin β	=	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Видео:Треугольники. 7 класс.Скачать

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	=	OE	=	OF	=	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Видео:Геометрия 7 класс (Урок№6 - Смежные и вертикальные углы. Аксиомы и теоремы.)Скачать

Вертикальные треугольники в геометрии

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

Развернутый угол — угoл, стороны которого лежат на одной прямой.
Прямой угoл — угoл, который равен половине развернутого угла.
Острый угол — угoл меньше прямого угла.
Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема. Вертикальные углы равны.

Свойства смежных и вертикальных углов

Углы при пересечении двух прямых секущей

Вы смотрели конспект по геометрии «Угол. Смежные и вертикальные углы». Использованы цитаты из учебных пособий:

Цитирование указанных пособий произведено в учебных целях (часть 1 статьи 1274 Гражданского кодекса РФ) с указанием авторства, источника заимствования и ссылки на покупку учебного пособия в крупнейшем книжном Интернет-магазине. Выберите дальнейшие действия: