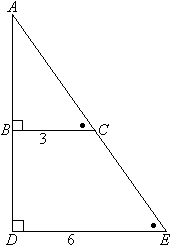Легкие задачи на треугольники

Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники

Запомните!

1. Признаки равенства треугольников.

• 1-й. По двум сторонам и углу между ними.
• 2-й. По стороне и двум прилежащим к ней углам.
• 3-й. По трем сторонам.

2. Свойство углов равнобедренного треугольника.

Углы при основании равнобедренного треугольника равны.

3. Обратная теорема.

Если два угла треугольника равны, то треугольник равнобедренный.

4. Свойство биссектрисы равнобедренного треугольника.

Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.

5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:

• а) высота является и медианой;
• б) высота является и биссектрисой;
• в) биссектриса является и медианой.

6. Теорема о свойстве точек серединного перпендикуляра.

• Любая точка серединного перпендикуляра равноудалена от концов отрезка.
• Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.

7. Теорема о пересечении серединных перпендикуляров.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.

Простые вопросы по теме «Треугольники»

1. В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
2. Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
3. Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
4. Может ли высота треугольника делить сторону пополам?
5. Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
6. Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
7. Является ли любой равнобедренный треугольник равносторонним?
8. Является ли любой равносторонний треугольник равнобедренным?
9. Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
10. Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
11. Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
12. Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
13. Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
14. Что для студентов означает слово «медиум»?
15. Сколько всего теорем в данной теме?

Непростые вопросы по теме «Треугольники»

16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?

Ответы на простые и непростые вопросы

1. Три. Два маленьких и один данный.
2. 12; 24.
3. Да.
4. Да. В равнобедренном треугольнике.
5. Да. В равнобедренном треугольнике.
6. Нет. Только биссектриса, проведенная из вершины к основанию.
7. Нет.
8. Да.
9. Да. Если треугольник равносторонний.
10. Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
11. Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
12. Да. Например, равносторонний.
13. 90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
14. Медиум — студенческий праздник, знаменующий середину учебы.
15. Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.

16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.

Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия:

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Решение задач по теме «Треугольники» (7-й класс)

Разделы: Математика

Класс: 7

Цели и задачи урока:

• обобщить, закрепить и углубить знания по изученной теме;
• формировать умение обучаемых доказывать равенство данных треугольников, опираясь на изученные признаки, применять свойства равнобедренного треугольника;
• отработать навыки решения простейших задач на построение с помощью циркуля и линейки;

• развивать логическое мышление, самостоятельность учащихся при решении заданий; умение на практике применять знания, полученные на уроках;

• воспитывать познавательную активность, упорство в достижении поставленной цели, культуру умственного труда

Оборудование:

• интерактивная доска или наглядный материал (готовые чертежи);
• карточки с задачами для индивидуальной работы на доске;
• таблицы с признаками равенства треугольников.

Тип урока: урок закрепления полученных знаний.

Ход урока

І. Организационный момент.

Учитель:

— Тема урока: «Решение задач по теме «Треугольники»». Мы сегодня обобщим и систематизируем знания по данной теме и наша цель: подготовиться к контрольной работе, которая будет на следующем уроке.

— Откройте дневники и запишите домашнее задание.

• I уровень: № 120(б), 121;
• II – III уровень: №160 (б), 162(б).

II. Актуализация опорных знаний.

1. У доски двое учащихся решают задачи по карточкам.

Начертите равнобедренный треугольник АВС с основанием АС. С помощью циркуля и линейки проведите медиану АА1 к боковой стороне ВС.

Дано: АО = BO, СО = DO, CO = 5см, ВО = 3см, BD = 4см.
1)Докажите, что САО = DBO.
2)Найдите периметр треугольника САО.

2. Для остальных учащихся класса организована фронтальная работа.

Цель: повторить основные вопросы теории темы «Равнобедренный треугольник и его свойства» с помощью теста. (Вопросы теста – на интерактивной доске)

Теоретический тест. [1]
В каждом задании из трёх предложенных ответов выберите верный и обоснуйте его. Верных ответов может быть несколько. Подумайте и ответьте на вопрос. (А я считаю, что…; я не согласна с этим утверждением, т.к. …)

1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: б), если медиана проведена к основанию равнобедренного треугольника.

2) Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой.
Ответ: а), б), и в), равносторонний треугольник является частным случаем равнобедренного треугольника; в равнобедренном треугольнике углы при основании равны, поэтому в равностороннем треугольнике все углы равны.

3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: б), высота, проведённая к основанию равнобедренного треугольника.

4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: а)

5) Если треугольник равнобедренный, то
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
Ответ: в), т.к. равнобедренный треугольник не всегда является равносторонним; медиана, проведённая к боковой стороне равнобедренного треугольника, не является биссектрисой и высотой, если треугольник не равносторонний.

6) В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: в).

Учитель:
— Мы с вами повторили материал темы «Равнобедренный треугольник и его свойства», а теперь повторим признаки равенства треугольников. (Обратить внимание обучающихся на таблицы с признаками равенства треугольников)

3. Задачи в рисунках (на интерактивной доске).

Учитель:
— Определите, являются ли равными треугольники на рисунках.

— Сколько пар равных элементов должно быть в равных треугольниках?

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Подобные треугольники

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Определение

Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

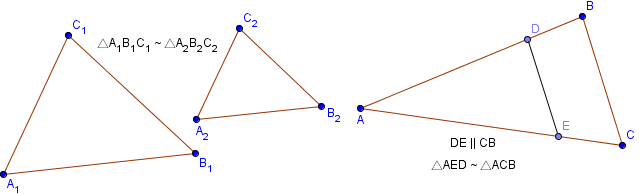
Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Практические задачи с подобными треугольниками

Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

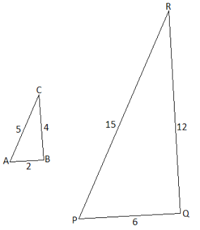
Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac = frac = frac = frac = frac Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac = frac = frac Rightarrow CA = frac = 23.57$
x = AC — DC = 23.57 — 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac = frac = frac Rightarrow AB = frac = 24 м$
x = AB — 8 = 24 — 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt = 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

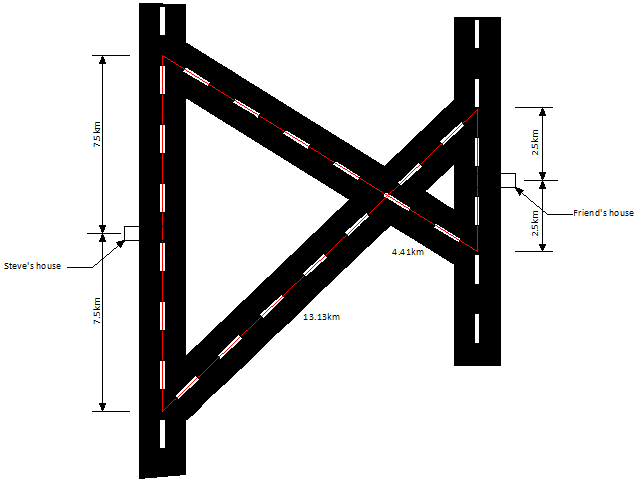
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

Пример 7:
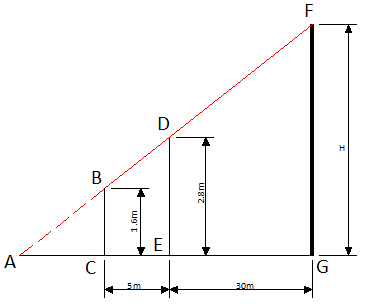
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.

Решение:

Геометрическое представление задачи показано на рисунке.

Сначала мы используем подобность треугольников ΔABC и ΔADE.

$frac = frac = frac = frac Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$

$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac = 6.67$

Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.

🔍 Видео

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать

Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Найдите угол: задача по геометрииСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Подобные треугольникиСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать