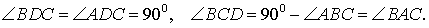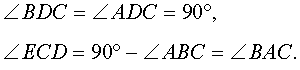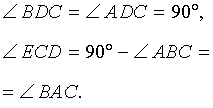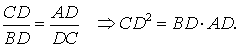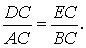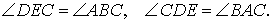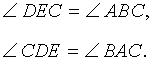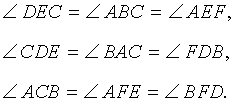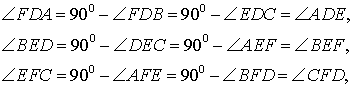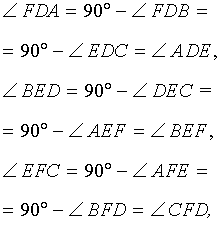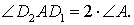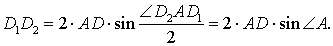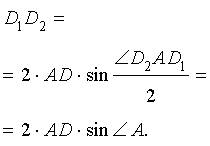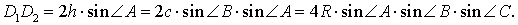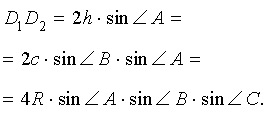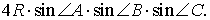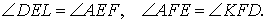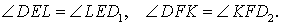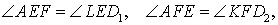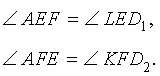- Что такое тупоугольный треугольник
- Элементы тупоугольного треугольника
- Формулы площади тупоугольного треугольника
- Пример решения задачи
- Тупоугольный треугольник
- Как найти вершины тупоугольного треугольника
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
- Задача Фаньяно
- Определения
- Пример решения задачи
- Что мы узнали?
- Тест по теме
- Оценка статьи
- Содержание
- Бонус
- 🌟 Видео
Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Что такое тупоугольный треугольник
Тупоугольный треугольник — геометрическая фигура на плоскости, которая представляет собой треугольник, один из углов которого является тупым, то есть больше 90º.
Такой треугольник не может быть прямоугольным и равносторонним, но может быть равнобедренным.
Сумма углов треугольника равна 180º. Именно поэтому только один из них может быть больше 90º, два других всегда острые. Это единственная особенность данной фигуры. Подход к решению задач с такой фигурой не отличается от решения задач с треугольниками других типов.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Элементы тупоугольного треугольника
Помимо сторон и углов, тупоугольный треугольник имеет следующие элементы:
- Внешний угол — тот, который смежен с внутренним, всего их шесть, по два на один внутренний. Внешний угол тупого всегда будет острым, острого — тупым.
- Медиана — отрезок, который соединяет вершину треугольника с противолежащей стороной и делит ее пополам. Все медианы пересекаются друг с другом в одной точке (центроиде). Эта точка делит медианы в соотношении 2:1, считая от вершины.
- Высота — перпендикуляр, который проведен из высоты треугольника на противоположную сторону. В тупоугольном треугольнике может лежать за пределами фигуры.
- Биссектриса — прямая, делящая угол пополам. Делит противоположную сторону на отрезки, которые пропорциональны прилежащим сторонам фигуры. Точка, которая является пересечением биссектрис, также является центром вписанной окружности.
Видео:Высота медиана биссектриса в тупоугольном треугольникеСкачать

Формулы площади тупоугольного треугольника
Для нахождения площади, периметра и других показателей тупоугольного треугольника используются те же формулы, что и для вычисления любого произвольного треугольника.
Площадь данной фигуры можно найти при помощи следующих формул:
S = ½ * x * h , где х — сторона;
S = √ p * ( p — x ) * ( p — y ) * ( p — z ) ,
p — полупериметр, p = ( x + y + z ) / 2
S = x * y * z / 4 * R , R — радиус описанной окружности;
S = p * r , p — полупериметр, r — радиус вписанной окружности.
Видео:№300. Докажите, что в тупоугольном треугольнике основание высоты, проведенной из вершины тупого углаСкачать

Пример решения задачи
Найти площадь тупоугольного треугольника, у которого стороны равны x=9, y=5, z=6.
Для решения задачи стоит использовать формулу площади с полупериметром.
p = ( x + y + z ) / 2 , p = ( 9 + 5 + 6 ) / 2 = 20 / 2 = 10 .
S = √ p * ( p — x ) * ( p — y ) * ( p — z ) , S = √ 10 * ( 10 — 9 ) * ( 10 — 5 ) * ( 10 — 6 ) = √ 10 * 1 * 5 * 4 = √ 200 = 10 √ 2
Видео:Построение высоты в треугольникеСкачать

Тупоугольный треугольник
Определение тупоугольного треугольника
Тупоугольным треугольником называется треугольник, у которого один уз углов тупой (т.е. больше
Медиана тупоугольного треугольника, проведённая из вершины тупого угла, меньше половины стороны, на которую она опущена.
Примеры решения задач
Выяснить, является ли треугольник тупоугольным, если его стороны равны ( mathrm=9 ) см, ( mathrm=5 ) см и ( c=6 ) см.
Так в треугольнике против большего угла лежит большая сторона, то запишем теорему косинусов для стороны a:
( 81=25+36-2 cdot 5 cdot 6 cdot cos alpha )
откуда ( cos alpha=-frac ) . Так как значение косинуса отрицательное, то угол а тупой.
Докажите, что в тупоугольном треугольнике основание высоты, проведенной из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведенных из вершин острых углов, – на продолжениях сторон.
Теперь допустим, что в том же треугольнике основание высоты ( mathrm ) лежит на продолжении стороны ( mathrm ), например, за точкой C. Так как ( angle C ) – острый, то угол смежный с ним – тупой. Тогда в прямоугольном треугольнике ( mathrm ) есть тупой угол. Это невозможно, поэтому точка ( mathrm ) лежит на стороне ( mathrm ).
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Как найти вершины тупоугольного треугольника
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:Построение медианы в треугольникеСкачать

Высота треугольника. Свойство высоты прямоугольного треугольника
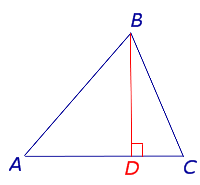
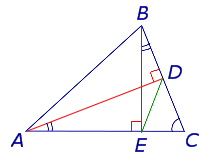
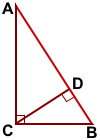
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
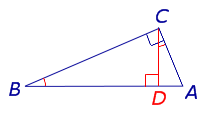
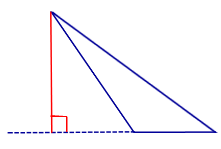
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 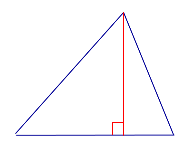 | Все высоты остроугольного треугольника лежат внутри треугольника. |
 | ||
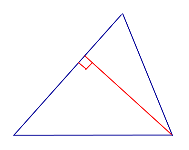 | ||
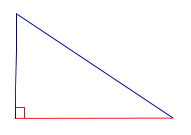
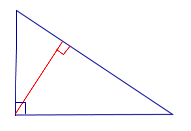
| Прямоугольный треугольник | 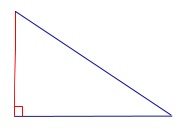 | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
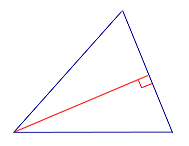
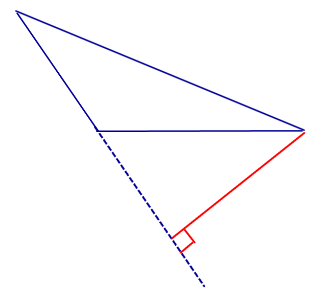
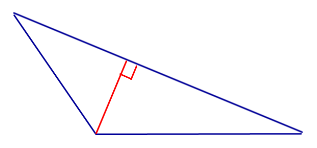
| Тупоугольный треугольник | 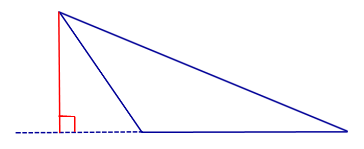 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Высота в тупоугольном треугольнике #егэ #математика #умскулСкачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:Свойство высоты в прямоугольном треугольникеСкачать

Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 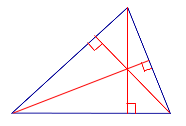 |
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
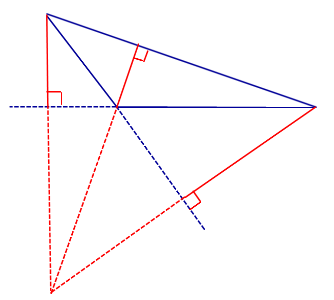
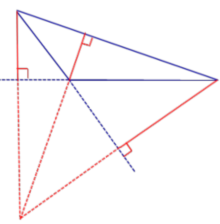
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Ортоцентрический треугольник
Решим следующую задачу.
Задача . В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC .
Решение . Рассмотрим треугольники ADC и BEC . Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
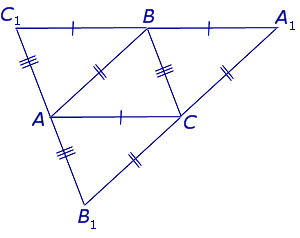
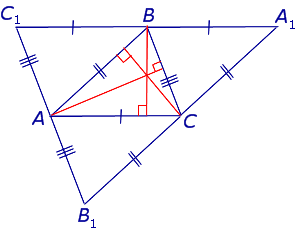
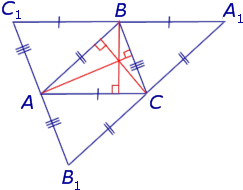
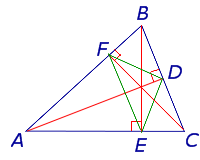
Определение 3 . Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Из определения 3 и следствия 1 вытекает следствие 2.
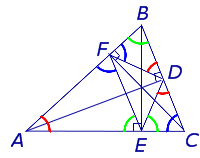
Следствие 2 . Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
Теорема 2 . Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство . Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Задача Фаньяно
Задача Фаньяно . Рассматриваются всевозможные треугольники DEF , вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC .
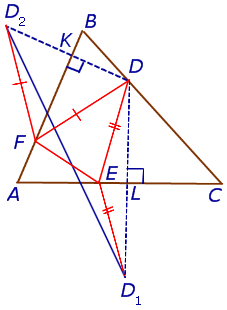
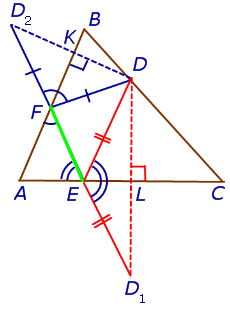
Решение . Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC , и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2 . Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF , вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Заметим также, что выполнено равенство
Кроме того, выполнено равенство
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC . Другими словами, наименьшим периметром обладает такой треугольник DEF , у которого вершина D является основанием высоты треугольника ABC , проведённой из вершины A , а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A , длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
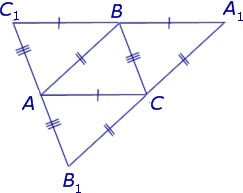
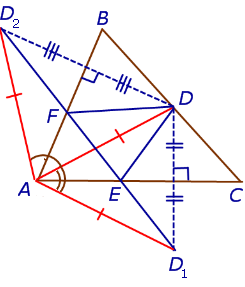
Лемма . Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
В этом случае отрезок D1D2 проходит через точки F и E .
Доказательство . Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2 , а также в силу равенства треугольников DEL и LED1 выполняются равенства:
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1 , F, E , D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.
Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.
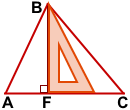
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.
Все высоты треугольника пересекаются в одной точке.
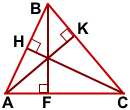
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.
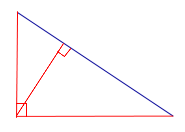
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.
Точка пересечения высот прямоугольного треугольника — вершина прямого угла.
Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.
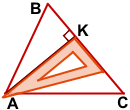
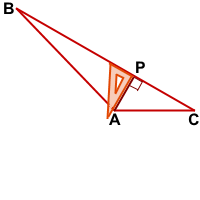
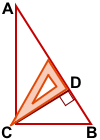
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.
Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.
AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.
Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.
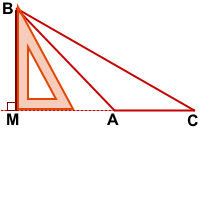
Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.
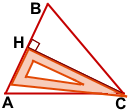
Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.
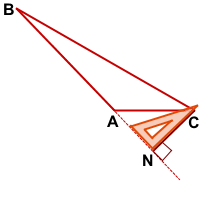
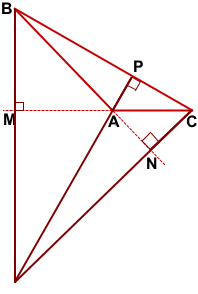
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.
Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.
Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.
Мы рассмотрели, как строить высоты треугольника с помощью угольника.
Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».
Видео:Тупоугольный треугольник для острого умаСкачать

Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном это обычный треугольник и подход к решению таких фигур ничем не отличается.
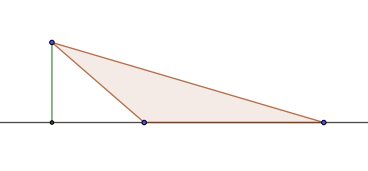
Рис. 1. Тупоугольный треугольник.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
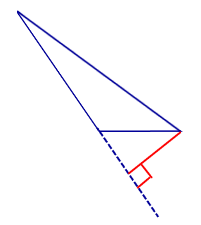
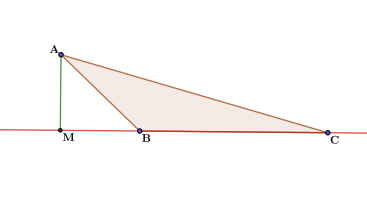
Рис. 2. Высота в тупоугольном треугольнике.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Пример решения задачи
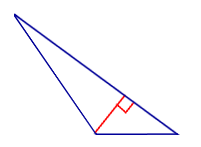
Рис. 3. Рисунок к задаче.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
- Второй способ это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем через значение косинуса найти значение синуса того же угла. А синус это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза это сторона АВ прямоугольного треугольника.
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
- Третий метод это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$sqrt =sqrt =sqrt =3sqrt $$ – по теореме косинусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
Выразим искомый синус угла АСВ.
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
Ответы всех трех способов совпали, а значит задача решена верно.
Видео:Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать

Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а так же выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Видео:пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать

Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 134.
Не понравилось? — Напиши в комментариях, чего не хватает.
Видео:Геометрия 7.Треугольники урок 6. Высота треугольника. Определение, свойства, точки пересечения высотСкачать

Содержание
- Определения
- Пример решения задачи
- Что мы узнали?
Бонус
- Тест по теме
- Площадь прямоугольного треугольника
- Высота треугольника
- Площадь правильного треугольника
- Площадь прямого треугольника
- Площадь равностороннего треугольника
- Площадь равнобедренного треугольника
- Медиана треугольника
- Правильный треугольник Тупоугольный треугольник
- Остроугольный треугольник
- Свойства прямоугольного треугольника
- Стороны прямоугольного треугольника
- Средняя линия прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Высота равностороннего треугольника
- Медиана равностороннего треугольника
- Неравенство треугольника
- Длина медианы правильного треугольника
- Равнобедренный тупоугольный треугольник
- Средняя линия прямоугольного треугольника
- Длина средней линии треугольника
По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.
- 1.
Михаил Тяпин 214
- 2.
Наталия Дробот 198
- 3.
Мария Кауфман 192
- 4.
Игорь Проскуренко 157
- 5.
Соня Зверева 153
- 6.
Василиса Варавкина 119
- 7.
Иоанн Стефановский 107
- 8.
Софья Холена 94
- 9.
Оля Проскурина 85
- 10.
Татьяна Бежина 83
- 1.
Мария Николаевна 13,500
- 2.
Лариса Самодурова 12,695
- 3.
Liza 12,310
- 4.
Кристина Волосочева 11,445
- 5.
TorkMen 11,441
- 6.
Ekaterina 11,176
- 7.
Влад Лубенков 11,100
- 8.
Лиса 11,070
- 9.
Юлия Бронникова 11,060
- 10.
Вячеслав 10,840
Самые активные участники недели:
- 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
- 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
- 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.
Три счастливчика, которые прошли хотя бы 1 тест:
- 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
- 2. Николай З — подарочная карта книжного магазина на 500 рублей.
- 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.
Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.
🌟 Видео
8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать

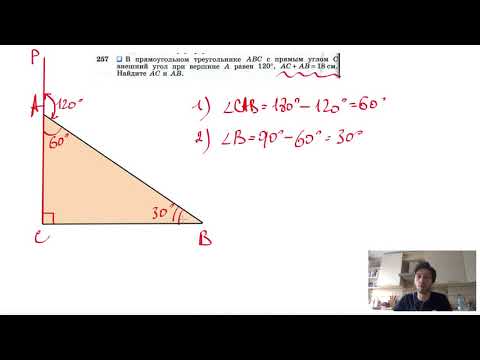
№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать