Верно ли что если некоторая прямая параллельна обеим плоскостям то она параллельна

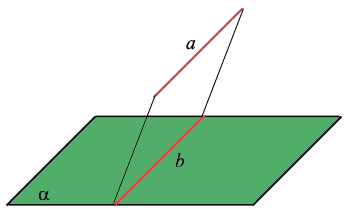
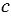Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

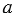
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.

Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

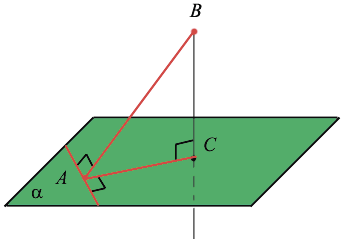
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

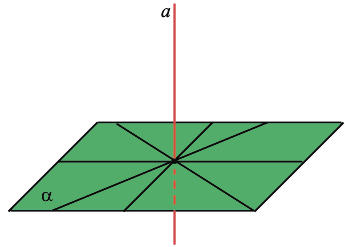
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения?

Геометрия | 5 — 9 классы

Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.

Пусть это не так.

Очевидно, что прямая не может пересекать прямую пересечения плоскостей, так как в этом случае она не будет параллельна плоскостям.

Пусть они скрещиваются.

Через прямую, скрещивающуюся с данной можно провести только одну плоскость, параллельную данной прямой, значит, 2 плоскости совпадают.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них?

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости?

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

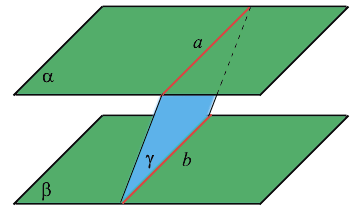
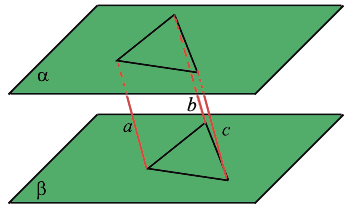
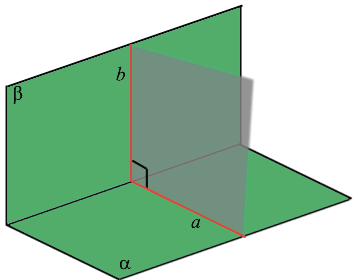
Плоскости Альфа и Бета пересекаются по прямой С?

Плоскости Альфа и Бета пересекаются по прямой С.

Плоскость Омега, параллельная прямой С, пересекает плоскости Альфа и Бета по прямым а и b соответственно.

Докажите, что a параллельна Бета и b параллельна Альфа.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а?

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а.

Докажите , что и плоскость в пересекает прямую а.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой?

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания?

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания.

Видео:№95. Прямая а параллельна плоскости α. Докажите, что если плоскость β пересекает прямую а, то онаСкачать

Помогите кто нибудь пожалуйста?

Помогите кто нибудь пожалуйста!

Докажите, что Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью?

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью.

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость?

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость.

Видео:№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

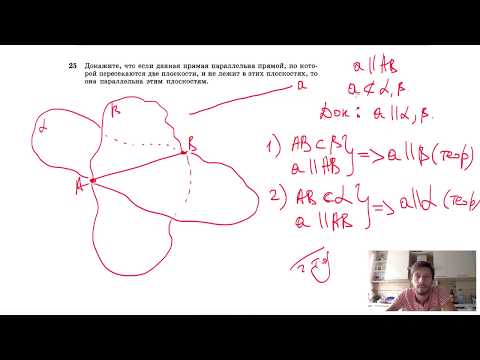
Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему)?

Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему).

Вы зашли на страницу вопроса Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Угол САВ = 180 — 94 = 86 * Треугольник АВС — равнобедренный следовательно угол А равен углу В следовательно угол В = углу А = 86. Сумма углов треугольника равна 180 * . Следовательно угол АСВ = 180 — А — В = 180 — 86 — 86 = 8. Угол АСВ = 8 * Угол ..

Нехай кут А і С — кути при основі, тоді кут А = С = 180 — 94 = 86градусів Кут В — протилежний до основи, кут В = 180 — 86 * 2 = 8 Зовнішній кут при вершині В = 180 — 8 = 172 градуси В — дь : 172.

Они будут н л , они равны а ост. Смежные их сумма равна 180° = > 180° — 43° =.

Пусть биссектриса х. Стороны треугольника a, b, c a + b + c = 36 (периметр треугольника) a + b + c + 2x = 24 + 30 (периметры двух треугольников, на которые разбивает биссектриса данный треугольник) 36 + 2х = 54 2х = 54 — 36 2х = 18 х = 18 : 2 х = 9 ..

Решение в прикрепленном файле.

Трапеция прямоугольная = > два угла, прилежащие к одной боковой стороне, по 90°, Сумма углов, прилежащих​ к другой боковой стороне, = 180° 180° — 100° = 80° четвертый угол. Ответ : 90°, 90°, 80° и 100°.

Видео:Параллельность прямой к плоскостиСкачать

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Видео:Параллельность прямых. 10 класс.Скачать

Параллельные прямые и плоскость – основные сведения

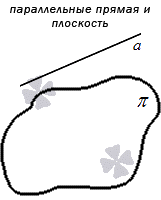
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10 — 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .

Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) — нормальным вектором заданной плоскости альфа.

Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.

Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) — нормальным вектором плоскости α .

Определить, параллельны ли прямая x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , — 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( — 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .

Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ имеют значения a → = ( 2 , 3 , — 4 ) .

Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( — 4 ) · 5 = 0 .

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , — 1 , — 7 ) .

По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .

Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , — 4 , — 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , — 4 , — 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.

Запишем A B → , i → = 2 · 1 + ( — 4 ) · 0 + ( — 7 ) · 0 = 2 ≠ 0 .

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α — общим уравнением плоскости A x + B y + C z + D = 0 .

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .

Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.

Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x — 1 = y + 2 — 1 = z 3 параллельна плоскости 6 x — 5 y + 1 3 z — 2 3 = 0 .

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

x — 1 = y + 2 — 1 = z 3 ⇔ — 1 · x = — 1 · ( y + 2 ) 3 · x = — 1 · z 3 · ( y + 2 ) = — 1 · z ⇔ x — y — 2 = 0 3 x + z = 0

Чтобы доказать параллельность заданной прямой x — y — 2 = 0 3 x + z = 0 с плоскостью 6 x — 5 y + 1 3 z — 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x — y — 2 = 0 3 x + z = 0 6 x — 5 y + 1 3 z — 2 3 = 0 .

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1 — 1 0 2 3 0 1 0 6 — 5 1 3 2 3

1 — 1 0 2 0 3 1 — 6 0 1 1 3 — 11 1 3

1 — 1 0 2 0 3 1 — 6 0 0 0 — 9 1 3 .

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x — 1 = y + 2 — 1 = z 3 и плоскость 6 x — 5 y + 1 3 z — 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

📺 Видео

6. Параллельность прямой и плоскостиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

№124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярныеСкачать

3.1 Признак параллельности плоскостейСкачать

№51. Докажите, что плоскости α и β параллельны, если две пересекающиеся прямые mСкачать