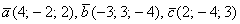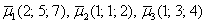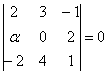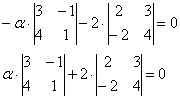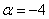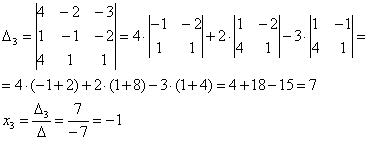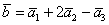Векторы не образуют базис

Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.

Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.

И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 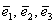, они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов!

Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)

Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают.

Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).

Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (почему?).

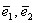
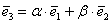
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга.

И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в этом базисе. Также говорят, что вектор представлен в виде линейной комбинации базисных векторов.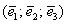

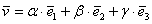
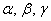
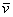
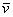
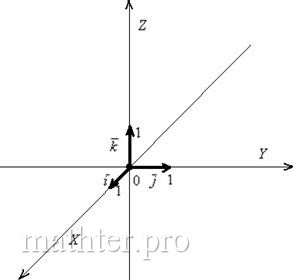
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов:

Выбранное (где угодно) начало координат , и некомпланарные векторы , взятые в определённом порядке, задают аффинную систему координаттрёхмерного пространства:

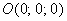
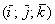
Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат и ортонормированный базис задают декартову прямоугольную систему координат пространства:

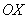
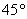
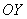
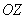
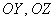
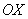
Ось абсцисс изображают под углом в по отношению к другим осям (к оси ординат и оси аппликат ). Популярный «тетрадный» масштаб: 1 ед. = 2 клетки по осям и 1 ед. = диагональ одной клетки – по оси .

И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:

Для трёх векторов пространства эквиваленты следующие утверждения:

1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.

Противоположные высказывания, думаю, понятны.

Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры:

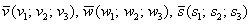
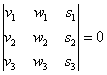
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: .

Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.

Задача 42

Проверить, образуют ли векторы базис трёхмерного пространства:

а)

б)

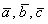
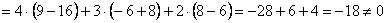
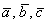
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):

, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.

Ответ: данные векторы образуют базис.

б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор.

Решим творческую задачку:

Задача 43

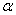
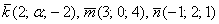
При каком значении параметра векторы будут компланарны?

Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:

По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:

Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:

Ответ: при

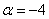
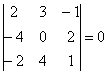
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.

И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии:

Задача 44

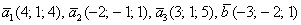
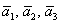
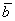
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.

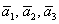
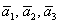
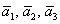
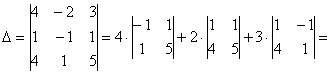
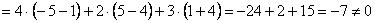
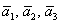
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать свой базис. И первый этап полностью совпадает с решением Задачи 42 – необходимо проверить, действительно ли векторы линейно независимы. Для этого нужно вычислить определитель, составленный из координат векторов :

, значит, векторы линейно независимы и образуют базис трехмерного пространства.

! Важно: координаты векторов 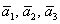обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

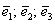
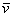
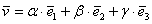
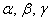
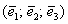
Теперь вспомним теоретическую часть: если векторы образуют базис, то любой вектор можно единственным способом разложить по данному базису: , где – координаты вектора в базисе .

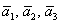
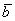
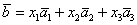
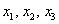
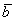
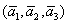
Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор можно единственным образом разложить по данному базису:
, где – координаты вектора в базисе .

И по условию требуется найти координаты .

Для удобства объяснения поменяю части местами: . В целях нахождения следует расписать данное равенство покоординатно:
– коэффициенты левой части берём из опр-ля ,
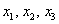
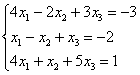
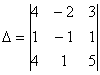
в правую часть записываем координаты вектора .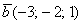

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден: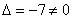
, значит, система имеет единственное решение.

Дальнейшее дело техники: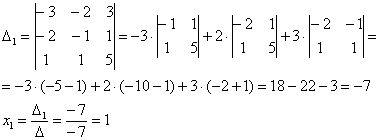


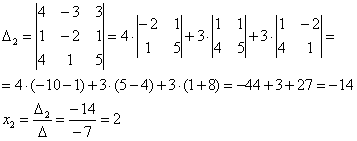
и ещё один определитель:

Таким образом:
– разложение вектора по базису .

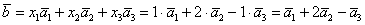
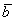
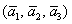
Ответ:

Такая же задача для самостоятельного решения:

Задача 45

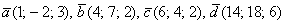
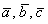
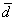
Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Онлайн калькулятор. Проверить образуют ли вектора базис.

Этот онлайн калькулятор позволит вам очень просто проверить образует ли заданый набор векторов базис (проверить линейную независимость векторов).

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на определение образует ли заданый набор векторов базис и закрепить пройденый материал.

Видео:Образуют ли данные векторы базисСкачать

Калькулятор для проверки образуют ли вектора базис (проверить линейную независимость векторов)

Выберите размерность пространства

Количество координат в векторе:

Введите значение векторов:

Инструкция использования калькулятора для проверки образуют ли вектора базис (проверки линейной независимости векторов)

• Для того чтобы проверить образуют ли вектора базис (проверить линейную независимость векторов) онлайн:
• выберите необходимую вам размерность пространства;
• введите значение векторов;
• Нажмите кнопку «Проверить образуют ли вектора базис» и вы получите детальное решение задачи.

Ввод данных в калькулятор для проверки образуют ли вектора базис (проверить линейную независимость векторов)

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора проверки образуют ли вектора базис (проверить линейную независимость векторов)

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Видео:Найдите разложение вектора по векторам (базису)Скачать

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

🎥 Видео

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Семинар 3 - Задача 3 (Какие из векторов образуют базис?)Скачать

Разложение вектора по базису. 9 класс.Скачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 7Скачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 6Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Линейная зависимость и линейная независимость векторов.Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 8Скачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Базис. Разложение вектора по базису.Скачать

Базис линейного пространства (01)Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать