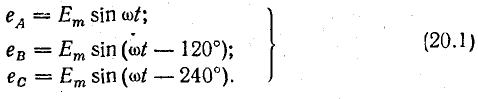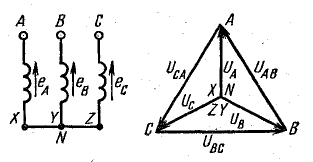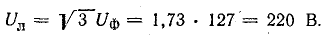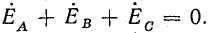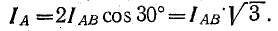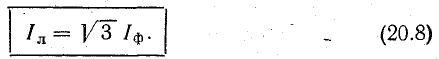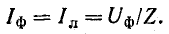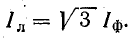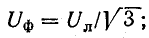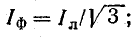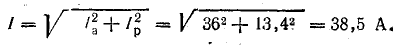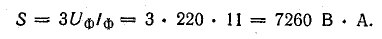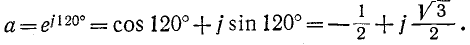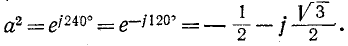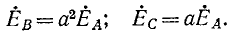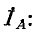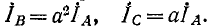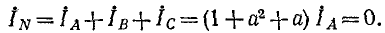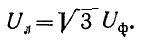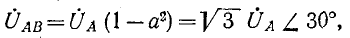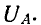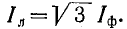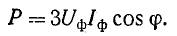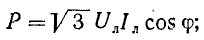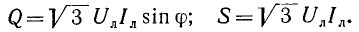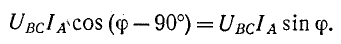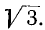Векторная диаграмма симметричного режима треугольника

Цепь трехфазного тока может содержать в себе различные компоненты. Для ее стабильной работы, необходимо правильно рассчитать все напряжения, нагрузки и иные параметры. Статья даст подробное описание, что такое векторная диаграмма для трехфазной цепи, опишет ее разновидности, способы расчета.

Видео:Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

Определение

Векторной диаграммой называют метод графического изображения расчета всех параметров цепи переменного тока в виде векторов. Данный метод предполагает изображение всех составных напряжений, токов и процессов в виде отложенных векторов на плоскости.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Назначение

Векторная диаграмма используется для расчетов напряжений, токов в трехфазной цепи и других цепях переменного тока. Метод помогает определить значение всех процессов, происходящих в схеме, их влияние на каждый проводник, нейтраль, а также провести расчет возникающих нагрузок.

Видео:Векторная диаграммаСкачать

Разновидности

Векторные диаграммы трехфазных сетей могут быть симметричными или несимметричными. Построение гистограммы прямо зависит от ее схемы. Разновидности цепей и их гистограмм описаны далее в статье.

Видео:Векторная диаграмма при соединении приемника треугольникомСкачать

Симметричные

Симметричные цепи переменного тока предполагают соединение 3 фаз от источника (генератора) с тремя приемниками.

При этом создаются совершенно независимые трехфазные схемы. При этом используется соединение трех фаз генератора звездой. Для симметричных схем должны соблюдаться требования:

1. Амплитуда должна быть для всех фаз одинаковой.
2. ЭДС должна иметь угол сдвига 120 градусов.
3. Угловые частоты должны быть равными.

Также учитывается принцип чередования ЭДС во времени. Если ротор генератора вращается по часовой стрелке (правое вращение), то происходит чередование прямого типа (A, B, C). Такая система считается симметричной.

Если ротор вращается против часовой стрелки (левое вращение), чередование считается обратным (A, C, B), но общая система ЭДС остается все так же симметричной.

Для симметричных схем применяется расчет по векторной гистограмме, приведенной ниже.

Видео:Как снять векторную диаграммуСкачать

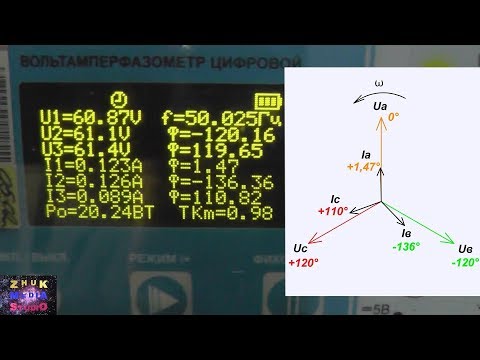
Несимметричные

Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:

1. Увеличение сопротивления нейтрали.
2. Полное отсутствие проводимости.
3. Увеличение напряжения.
4. Максимальное искажение фазных напряжений.

При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.

Ниже приведена векторная диаграмма несимметричной цепи.

Видео:Построение векторной диаграммы. Цепь RLCСкачать

Построение диаграммы

Векторная диаграмма предполагает в своей основе следующие значения:

1. Точку начала отсчета N для всех трех отдельных фаз.
2. Векторное направление ABC как отдельных проводников источника напряжения (генератора). Каждый вектор имеет заданную длину, равную своему напряжению.
3. Окончание векторов AВ, BС, CА, как приемников напряжения.

Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.

А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.

Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.

Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Заключение

Если вы работаете с трехфазными цепями, то векторная диаграмма используется для получения визуального отображения всех действующих процессов в таких цепях переменного трехфазного тока. Такая диаграмма полезна при определении несоответствий схемы между углами сдвига фаз, напряжениями и токами.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Видео по теме

Видео:РЗ #35 Защита от ОЗЗ в сетях с изолированной нейтральюСкачать

Трехфазные симметричные цепи

Содержание:

Трехфазные симметричные цепи:

Основными приемниками электрической энергии как по количеству, так и по установленной мощности являются электродвигатели, применяемые для приведения в движение рабочих машин. Трехфазные асинхронные двигатели — наиболее простые, надежные и дешевые. Повсеместное применение их обусловило бурное развитие трехфазных систем — производства, передачи и распределения электрической энергии. Для этой цели применяются трехфазные генераторы, трансформаторы, линии передачи, распределительные сети.

Видео:Как построить векторную диаграмму напряжений?Скачать

Общие сведения о трехфазных системах

Многофазная система электрических цепей представляет собой совокупность электрических цепей, в которых действуют синусоидальные э. д. с. одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые одним источником энергии. Соответствующая этому определению система из трех цепей называется трехфазной.

Трехфазная система э. д .с.

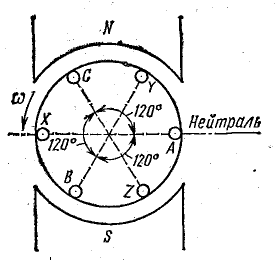
В трехфазном генераторе, в котором имеются три самостоятельные обмотки, сдвинутые относительно друг друга в пространстве на 120°, образуется трехфазная симметричная система э. д .с. Схематично это показано на рис. 20.1 применительно к генератору с одной парой полюсов на статоре и обмотками на роторе. Однако нужно заметить, что в реальных генераторах обмотка переменного тока неподвижна (расположена на статоре), а магнитные полюса вращаются (расположены на роторе). Такая конструкция генератора лучше, а принцип его работы не меняется.

Если число витков в обмотках одинаково, то при вращении ротора во всех обмотках наводятся э. д. с. одинаковой величины. Начальные фазы этих э. д. с. сдвинуты относительно друг друга на 120° в соответствии с пространственным расположением обмоток.

Трехфазная симметричная система э. д. с. — это совокупность трех э. д. с., имеющих одинаковую частоту и амплитуду, сдвинутых по фазе относительно друг друга на углы 120°.

Признаком нессимметрии трехфазной системы э. д. с. является неравенство амплитуд или неравенство углов сдвига фаз между каждой парой э. д. с.
На рис. 20.1 обмотки показаны в начальном положении (t = 0). При вращении ротора против часовой стрелки уравнения э. д. с. можно записать в следующем виде:

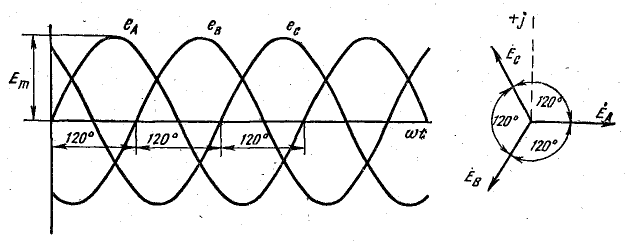
Рис. 20.2. Графики и векторная диаграмма симметричной системы э. д. с.

Несвязанная трехфазная система электрических цепей

На схемах замещения обмотки трехфазного генератора обозначают, как показано на рис. 20.3, а, и условно принимают направление э. д .с. от конца к началу обмотки положительным.

Если каждую обмотку трехфазного генератора соединить со своим приемником, образуются три независимые цепи, каждая со своим током. Одна такая цепь с ее элементами (обмотка генератора, приемник, соединительные провода) в практике называется фазой. Термин «фаза» употреблен в своем подлинном значении, которое остается в силе и для трехфазных цепей.
В несвязанной трехфазной системе генератор с приемником энергии соединяется шестью проводами. Большое число соединительных проводов — основной недостаток несвязанных систем, которые поэтому и не применяются. Сокращение числа соединительных проводов достигается в связанных системах, где обмотки генератора, как и отдельные фазы приемника, электрически связаны между собой и образуют трехфазные цепи.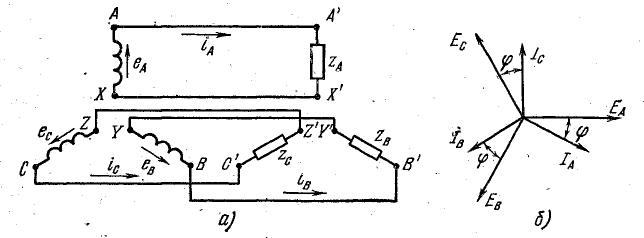

Рис. 20.3. Несвязанная трехфазная система электрических цепей

Для этой цели выдающимся русским ученым М. О. Доливо-Добровольским (1862—1919) предложены две схемы соединения: звездой и треугольником, которые применяются и в настоящее время.

Трехфазная цепь называется симметричной, если комплексы сопротивлений всех ее фаз одинаковы. Когда в такой цепи действует симметричная система э. д. с., то токи в фазах равны по величине и сдвинуты по фазе на угол 120°, т. е. получается симметричная трехфазная система токов (рис. 20.3, б).

Нужно отметить, что приемник электрической энергии (электродвигатели, электролампы и т. п.) с генераторами, установленными на электростанциях, обычно непосредственно не связаны.

На пути электроэнергии от генератора к приемникам установлены трансформаторы, с помощью которых в электрической сети неоднократно изменяется напряжение. Для указанных приемников источником электрической энергии чаще всего служат трехфазные трансформаторы, которые по отношению к генераторам сами являются приемниками энергии. Поэтому далее все рассуждения будем относить к -трехфазному источнику, подразумевая при этом генератор или трансформатор.

Соединение звездой при симметричной нагрузке

На рис. 20.4 показана связанная система при соединении фаз источника энергии и приемника звездой. Такую систему легко получить из несвязанной системы.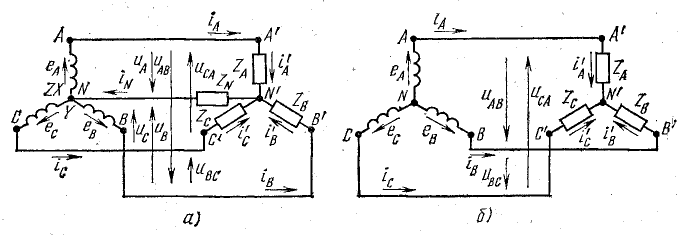

Рис. 20.4. Связанные трехфазные системы электрических цепей при соединении звездой

Концы обмоток источника X, Y, Z соединяются в общую точку N, называемую нулевой точкой или нейтралью. Провода, соединяющие начала А, В и С обмоток источника с приемником (линейные провода), сохраняются; три провода, присоединенные к концам обмоток, заменяются одним. Благодаря этому в приемнике также образуется нулевая точка N’ (нейтраль). Нулевые точки источника энергии и приемника могут быть связаны проводом, который называется нулевым или нейтральным (рис. 20.4, а). В этом случае получается связанная четырехпроводная трехфазная система электрических цепей.
Далее будет показано, что в симметричных трехфазных цепях можно отказаться от нулевого провода, так как ток в нем равен нулю. В этом случае связь между источником и приемником, соединенными звездой, можно осуществлять по трехпроводной схеме (рис. 20.4, б).

Фазные напряжения

Разность потенциалов между линейными зажимами и нейтралью называется фазным напряжением (, , ).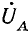

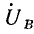
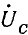
Фазные напряжения источника есть напряжения между началами и концами фаз, они отличаются от э. д. с. на величину падения напряжения в обмотках. Если сопротивлением обмоток можно пренебречь, то фазные напряжения источника равны соответствующим э. д. с. В симметричной системе они изображаются, так же как и э. д. с., тремя равными по величине векторами, сдвинутыми по фазе на 120° (рис. 20.5, а).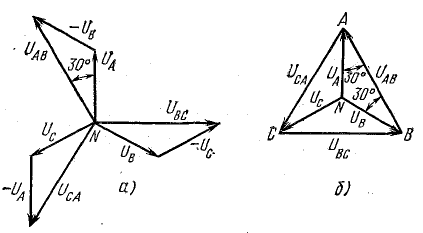

Рис. 20.5. Векторные диаграммы напряжений при соединении обмоток источника звездой

В четырехпроводной и симметричной трехпроводной цепях фазные напряжения в приемнике меньше, чем в источнике, на величину падения напряжения в соединительных проводах. Если сопротивлением проводов можно пренебречь, то фазные напряжения в приемнике считаются такими же, как в источнике.

Линейные напряжения

Разность потенциалов между каждой парой линейных проводов называется линейным напряжением (, , ).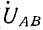

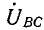
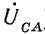
Если принять потенциал нулевой точки N источника энергии равным нулю, то потенциалы его линейных зажимов:

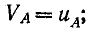
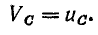
Линейные напряжения: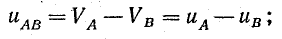



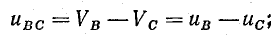
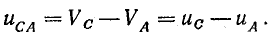
Переходя к действующим величинам, напишем выражения в комплексной форме: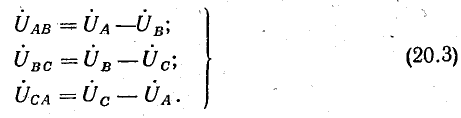

Потенциалы линейных зажимов (или линейных проводов) в каждое мгновение отличаются друг от друга из-за наличия сдвига фаз между фазными напряжениями. Следовательно, линейные напряжения не равны нулю. Их можно определить аналитически по уравнениям (20.3) или графически с помощью векторной диаграммы рис. 20.5.

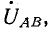
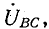
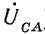
Из векторной диаграммы видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: равны по величине и сдвинуты относительно друг друга на 120°. Вместе с тем при прямой последовательности фаз звезда векторов линейных напряжений опережает на 30° звезду векторов фазных напряжений.

Векторную диаграмму удобно выполнить топографической, тогда каждой точке цепи соответствует определенная точка на диаграмме (рис. 20.5, б). Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжение между одноименными точками цепи.
Действующая величина линейных напряжений легко определяется по векторной диаграмме из треугольника, образованного векторами двух фазных и одного линейного напряжения, например ANB: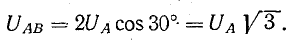

Обозначая все фазные напряжения U_ф, а линейные напряжения U_л получим общее соотношение между линейными и фазными напряжениями в симметричной системе

Фазные и линейные токи

В связанной системе (см. рис. 20.4, а), так же как и в несвязанной, каждая фаза представляет собой замкнутую цепь.

В соответствии с положительным направлением э. д. с. в обмотках источника положительное направление токов в линейных проводах — от источника к приемнику, а в нулевом проводе — от приемника к источнику.

В трехфазных цепях различают фазные и линейные токи.
Токи в фазах источника и приемника называют фазными (на рис. 20.4 i’_A, i’_B, i’_С; общее обозначение i_ф). Токи в линейных проводах называют линейными (i_A, i_B, i_С; общее обозначение i_л).

При соединении звездой в точках перехода из источника в линию и из линии в приемник нет разветвлений, поэтому фазные и линейные токи одинаковы между собой в каждой фазе:

Задача 20.3.

В каждой фазе трехфазного генератора наводится э. д. с. Е = 127 В. Начертить схему, построить векторную диаграмму и определить линейные напряжения при холостом ходе, если в общую точку соединены зажимы: а) X, Y, Z; б) X, Y, C; в) X, B, Z; г) X, B, C; д)A, B, C. Буквами A, B, C обозначены начала, а X, Y, Z — концы обмоток.

Рис. 20.6. К задаче 20.3

Рис. 20.7. К задаче 20.3

Решение. Схема генератора и векторная диаграмма при соединении в общую точку зажимов X, Y, Z показаны на рис. 20.6. Из векторной диаграммы видно, что линейные напряжения одинаковы:

При соединении в общую точку зажимов X, Y, C (рис. 20.7) фаза С включена началом в нулевой точке, поэтому вектор фазного напряжения этой фазы изображен на векторной диаграмме в положении, повернутом на 180° к нормальному, и обозначен U_Z. Из векторной диаграммы следует: U_AB = 220 В; U_BZ = 127; U_ZA = 127 В.

Соединение треугольником при симметричной нагрузке

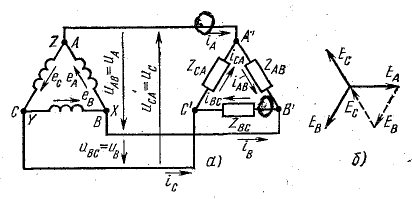
При соединении треугольником из трех обмоток источника образуется замкнутый на себя контур (рис. 20.8, а). Точно так же замкнутый контур создается из трех фаз приемника.

Общие точки двух фаз источника и двух фаз приемника соединяются между собой линейными проводами. Так образуется связанная трехфазная трехпроводная система, в которой каждая обмотка источника соединена с соответствующей фазой приемника парой линейных проводов, каждый из которых обеспечивает такую связь в двух смежных фазах.

Рис. 20.8. Связанная трехфазная система электрических цепей при соединении треугольником

Фазные и линейные напряжения

Соединение нескольких обмоток источника в замкнутый контур возможно лишь в том случае, если сумма всех э. д. с. этого контура равна нулю.
Это требование выполняется при таком порядке соединения, когда конец предыдущей обмотки соединяется с началом следующей. Например, конец X фазы А соединен с началом фазы В в общей точке ХВ, конец Y фазы В соединен с началом фазы С в общей точке YС и конец Z фазы С соединен с началом фазы А в общей точке ZА.

Симметричная система э. д. с., действующих в контуре, имеет сумму, равную нулю (рис. 20.8, б):

В этом случае при холостом ходе источника ток в его обмотках отсутствует.
При несимметрии системы э. д. с. их сумма не равна нулю, поэтому уже при холостом ходе в обмотках источника образуется ток, который может быть большим даже при малой несимметрии, так как сопротивление обмоток незначительно.

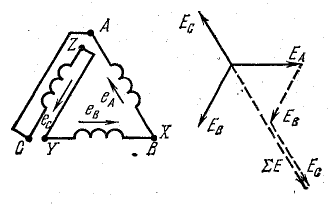
Рис. 20.9. Неправильное соединение треугольником обмоток источника

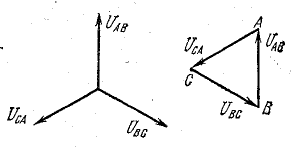
Рис. 20.10. Векторные диаграммы напряжений при соединении обмоток источника треугольником.

При неправильном включении обмоток, когда две соседние фазы соединены началами или концами (рис. 20.9), сумма э. д. с. в контуре равна удвоенной величине э. д. с. фазы.
Из схемы соединения треугольником видно, что фазные и линейные напряжения совпадают, так как конец одной фазы соединен с началом другой:

Векторную диаграмму напряжений можно построить в виде звезды или в виде замкнутого треугольника векторов (рис. 20.10). В последнем случае диаграмма является топографической.

Фазные и линейные токи

Каждая фаза приемника присоединении треугольником находится под линейным напряжением. Этим обусловлено наличие в приемнике фазных токов i_AB, i_BC, i_СA, положительное направление которых на схеме рис. 20.8 выбрано соответственно положительному направлению э. д. с. в фазах источника.

Точки А’, В’, С’ приемника, так же как и точки А, В, С источника, являются электрическими узлами, поэтому фазные токи отличаются от линейных i_A, i_B, i_С. Для узловых точек А, В, С можно написать уравнения в комплексной форме по первому закону Кирхгофа:

При симметричной нагрузке токи во всех фазах одинаковы. Звезда векторов линейных токов сдвинута относительно звезды фазных токов на 30° против вращения векторов, если последовательность фаз — прямая (рис. 20.11, а).
Действующая величина линейных токов определяется по векторной диаграмме из равнобедренного треугольника, образованного векторами двух фазных и одного линейного токов, например из треугольника ANC (рис. 20.11, б):

Рис. 20.11. Векторные диаграммы токов при соединении приемников треугольником

Обозначив все фазные токи I_ф, а линейные токи I_л, получим общее соотношение между линейными и фазными токами в симметричной цепи:

Расчет симметричных трехфазных цепей

Формулы (20.4) и (20.8), как уже отмечено, справедливы только для симметричных систем напряжений и токов.

Трехфазные электродвигатели имеют три одинаковые фазы обмотки, и создаваемая ими электрическая нагрузка симметрична. Нессимметрию создают однофазные приемники, например лампы электрического освещения и другие бытовые электроприемники. Если при проектировании осветительную нагрузку разделить между фазами поровну, то в процессе эксплуатации нагрузка, как правило, будет несимметричной из-за неодновременности включения ламп.

При большом числе однофазных приемников нессимметрия нагрузки, связанная с неодновременностью их включения, невелика, поэтому линии с напряжением 3; 6 кВ и выше, предназначенные для электроснабжения промышленных предприятий или определенного района (фидерные линии), выполняют трехпроводными независимо от схемы соединения групп приемников (звездой или треугольником).

Цель расчета состоит в определении токов в фазах приемника и проводах линии, а также мощности приемника в целом и в каждой фазе. Может быть поставлена и обратная задача.

Соединение звездой

В симметричной цепи комплексы сопротивлений фаз приемника одинаковы 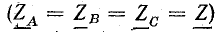и между зажимами приемника действует симметричная система линейных напряжений при любой схеме соединения источника (звездой или треугольником).

Поэтому на расчетной схеме источник (генератор или трансформатор) не показывают и говорят, что приемник включен в трехфазную сеть (см. рис. 21.3, о). (20.8)
В симметричной цепи достаточно провести расчет одной фазы, так как токи и мощности во всех фазах одинаковы.
При известном линейном напряжении U_л фазное напряжение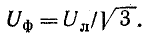

Фазный ток, равный линейному,

Соединение треугольником

При соединении треугольником фазное напряжение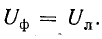
Ток в фазе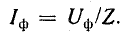

Линейный ток

Определение мощности

Мощность в каждой фазе трехфазной цепи определяется теми же формулами, которые применялись при расчете однофазных цепей.
При симметричной нагрузке фазные напряжения, токи и углы сдвига фаз между ними в каждой фазе одинаковы, поэтому при определении мощности цепи можно написать общие выражения: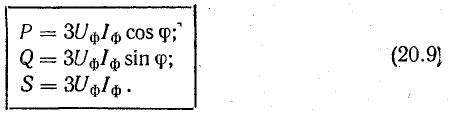

Учитывая, что при соединении звездой

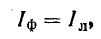
а при соединении треугольником

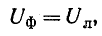
мощности можно определять через линейные величины напряжений и токов:

При решении задач символическим методом мощность определяется, так же как и в однофазных цепях, произведением соответствующих комплекса напряжения и сопряженного комплекса тока.

Задача 20.9.

К трехфазному трансформатору с линейным напряжением на вторичной обмотке 380 В включены звездой электрические лампы мощностью 40 Вт каждая (по 100 шт. в фазе) и трехфазный двигатель мощностью 10 кВт, имеющий к. п. д. 85%,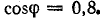
Пренебрегая сопротивлением проводов, определить токи в линии.
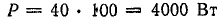
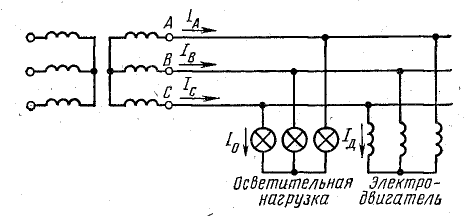
Решение. Заданная нагрузка симметрична, так как в каждой фазе включены одинаковые по величине и характеру приемники: осветительная нагрузка и одна фаза двигателя.

Рис. 20.12. К задаче 20.9

Расчет можно вести на одну фазу: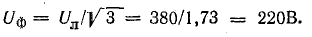

Ток осветительной нагрузки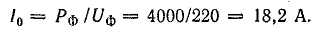

Ток в фазе двигателя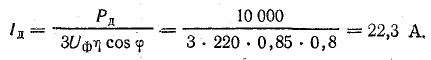

Для нахождения тока в линии нужно сложить токи ламп и двигателя. Эти токи по фазе не совпадают, поэтому разложим их на активные и реактивные составляющие и сложим одноименные составляющие.
Ток в лампах совпадает по фазе с напряжением, поэтому реактивный ток ламп I_0р = 0, активный ток I_0а = I₀ = 18,2 А.
Активный ток в фазе двигателя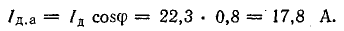

Реактивный ток в фазе двигателя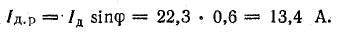

Общий активный ток. в линии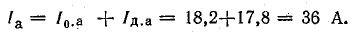

Общий реактивный ток в линии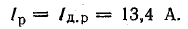

Ток в линии

Задача 20.12.

Приемник электрической энергии, соединенный треугольником, имеет активное сопротивление R = 12 Ом и емкость С = 199 мкФ. Определить: токи в фазах приемника и в линии, с помощью которой приемник подключен к сети с линейным напряжением U = 220 В и частотой f = 50 Гц; активную, реактивную и полную мощности приемника.
Решение.
Емкостное сопротивление фазы приемника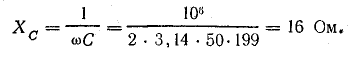

Полное сопротивление фазы приемника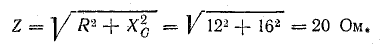

Фазное напряжение приемника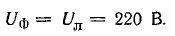

Фазный ток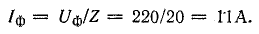

Линейный ток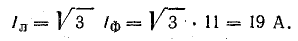

Мощность приемника:
активная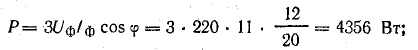

реактивная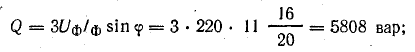

полная

Симметричный режим работы трехфазной цепи

Расчет трехфазной цепи, так же как и расчет всякой сложной цепи, ведется обычно в комплексной форме. Ввиду того что фазные э. д. с. генератора сдвинуты друг относительно друга на 120°, для краткости математической записи применяется фазовый оператор — комплексная величина

Умножение вектора на оператор а означает поворот вектора на 120° в положительном направлении (против хода часовой стрелки).

Соответственно умножение вектора на множитель а2 означает поворот вектора на, 240° в положительном направлении или, что то же, поворот его на 120° в отрицательном направлении.

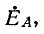
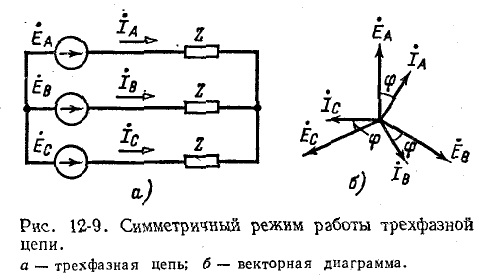
Если э. д. с. фазы А равна то э. д. с. фаз В и С равны соответственно:

В простейшем случае симметричного режима работы трехфазной цепи, когда генератор и нагрузка соединены звездой (рис. 12-9, а), векторная диаграмма э. д. с. и токов имеет вид, показанный на рис. 12-9, б.

Ток в каждой фазе отстает от э. д. с. той же фазы на

угол 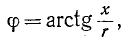где r и х — активное и реактивное сопротивления фаз.

* Кроме того, применяется понятие «фазное напряжение в данном сечении» трехфазной цепи по отношению к какой-либо точке, принимаемой за нуль, например земле, нулевой точке генератора или искусственной нулевой точке.

Ток в фазе А находят так же, как в однофазной цепи, потому что нейтральные точки генератора и нагрузки в симметричном режиме могут быть соединены как имеющие одинаковые потенциалы:

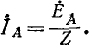
Соответственно токи в фазах В и С через ток

Наличие нейтрального провода «не вносит при симметричном режиме никаких изменений, так как сумма токов трех фаз равна нулю и ток в нем отсутствует:

Таким образом, при симметричном режиме работы трехфазной цепи задача сводится к расчету одной из фаз

аналогично расчету однофазной цепи. При этом сопротивление обратного (нейтрального) провода не учитывается, так как ток в нем и соответственно падение напряжения на нем отсутствуют.

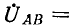
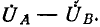
По мере удаления от генератора фазные напряжения, определяемые падениями напряжения до нейтральной точки нагрузки, изменяются по модулю (обычно убывают) и по фазе. Линейные напряжения определяются как разности соответствующих фазных напряжений, например: В любом месте трехфазной линии при симметричном режиме соблюдается следующее соотношение между модулями линейных и фазных напряжений:

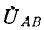
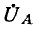
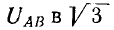
т. e. опережает по фазе а на 30°, причем модуль раз превышает

В случае соединения треугольником линейные токи определяются в соответствии с первым законом Кирхгофа как разности фазных токов и при симметричном режиме соблюдается соотношение

Соединение фаз генератора или нагрузки треугольником должно быть для расчета заменено эквивалентным соединением фаз звездой; вследствие этого расчет трехфазной цепи с соединением фаз треугольником приводится в конечном итоге к расчету эквивалентной трехфазной цепи с соединением фаз звездой.

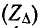
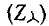
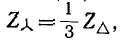
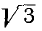
Между сопротивлениями сторон треугольника и лучей звезды имеет место соотношение вытекающее из формул преобразования треугольника сопротивлений в эквивалентную звезду. Это соотношение справедливо как для сопротивлений симметричной трехфазной нагрузки, так и для сопротивлений симметричного .трехфазного • генератора. При этом фазные э. д. с. эквивалентного генератора, соединенного звездой, берутся в раз меньшими фазных э. д. с. заданного генератора, соединенного треугольником (кроме того, они должны быть сдвинуты на угол 30°). Это легко усмотреть из векторной потенциальной диаграммы напряжений генератора.

Активная мощность симметричной трехфазной нагрузки равна:

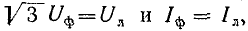
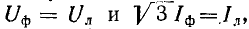
Ввиду того что при соединении нагрузки звездой а при соединении нагрузки треугольникомактивная мощность трехфазной цепи независимо от вида соединения выражается через линейные напряжения и ток следующим образом:

здесь 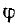— угол сдвига фазного тока относительно одноименного фазного напряжения.

Аналогичным образом для реактивной и полной мощностей симметричной трехфазной нагрузки имеем:

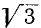
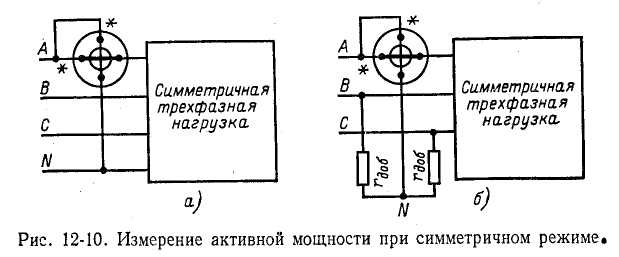
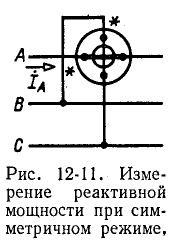
Приведенные выражения не означают, что при пересоединении нагрузки со звезды на треугольник (или наоборот) активная и реактивная мощности не изменяются. При пересоединении нагрузки со звезды на треугольник при заданном линейном напряжении фазные токи возрастут в раз, в линейный ток — в 3 раза и поэтому мощность возрастет в 3 раза.

Если нейтральная точка симметричной трехфазной нагрузки выведена, то измерение активной мощности может быть осуществлено одним ваттметром, включенным по схеме рис. 12-10, а (одноименные или так называемые генераторные выводы последовательной и параллельной цепей ваттметра отмечены на рис. 12-10, а звездочками). Утроенное показание ваттметра равно суммарной активной мощности трех фаз.

Если нейтральная точка не выведена или нагрузка соединена треугольником, то можно воспользоваться схемой рис. 12-10, б, где параллельная цепь ваттметра и два добавочных активных сопротивления 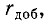равные по величине сопротивлению параллельной цепи ваттметра, образуют искусственную нейтральную точку

* Следует заметить, что здесь применим только электродинамический или ферродинамический ваттметр, сопротивление параллельной цепи которого является чисто активным. Индукционный ваттметр неприменим по той причине, что сопротивление параллельной цепи такого ваттметра имеет реактивное сопротивление; для создания искусственной нейтральной точки в этом случае потребовались бы реактивные добавочные сопротивления.

Для получения суммарной мощности, как и в предыдущем случае, показание ваттметра утраивается.

На рис. 12-11 показан способ измерения реактивной мощности в симметричной трехфазной цепи при помощи одного ваттметра: последовательная цепь ваттметра включена в фазу А, а параллельная — между фазами В и С, причем генераторные выводы ваттметра присоединены к фазам А и В.

Показание ваттметра в этом случае равно:

Для получения суммарной реактивной мощности показание умножается на

Разделив активную мощность на полную мощность, получим:

.
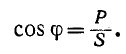
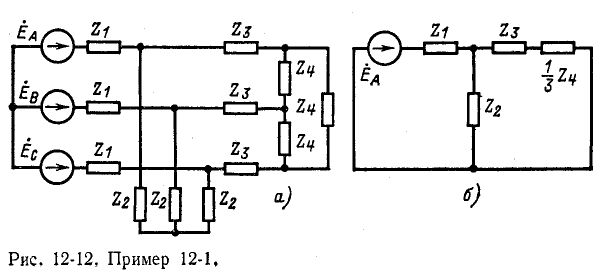
Пример 12-1. Определить ток в генераторе при симметричном режиме работы трехфазной цепи, представленной на рис, 12-12, а.

Сопротивления 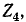соединенные треугольником, заменяются эквивалентной звездой из сопротивлений

При симметричном режиме нейтральные точки генератора и нагрузки, как было указано выше, могут быть объединены. Тогда режим работы каждой фазы, например фазы А, может быть рассмотрен в однофазной расчетной схеме (рис, 12-12, б),

Результирующее сопротивление цепи одной фазы равно:

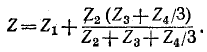
Искомый ток в фазе А

• Трехфазные несимметричные цепи
• Вращающееся магнитное поле
• Электрические цепи синусоидального тока
• Электрические цепи несинусоидального тока
• Принцип действия асинхронного и синхронного двигателей
• Метод симметричных составляющих
• Цепи периодического несинусоидального тока
• Резонанс токов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Векторные диаграммы Токов и Напряжений в программе VisioСкачать

Соединение потребителей электрической энергии в треугольник

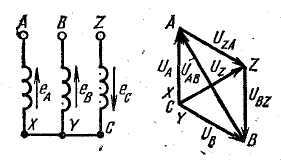
При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:

Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть U_Ф = U_Л. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.

На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.

В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:

Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.

Видео:Стереометрия за МЕСЯЦ?! Решаем задачи с 0 до ЕГЭСкачать

Симметричная нагрузка при соединении приемников треугольником

В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:

Очевидно, что при симметричной нагрузке:

Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:

В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения U_ab принято направлять вертикально вверх.

Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):

На основании данной векторной диаграммы можно записать: . Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке .

Пример

Трехфазная сеть имеет линейное напряжение U_Л = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное r_ф = 8,65 Ом и индуктивное x_ф = 5 Ом сопротивления.

Решение

Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.

Линейные и фазные токи, а также полные сопротивления фаз будут равны:

Активная, реактивная и полная мощности электроприемника любой фазы будут равны:

Векторные диаграммы приведены выше.

Видео:Зачем нужны векторные диаграммы?Скачать

Несимметричная нагрузка при соединении приемников треугольником

В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:

В пределах каждой группы подключение приемников производится параллельно.

После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:

Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:

Для определения суммарной мощности всех фаз нужно применять выражение:

Пример

Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: U_Л = 220 В, r_ab = 40 Ом, x_Lbc = 10 Ом, r_bс = 17,3 Ом, x_cа = 5 Ом, r_Ccа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.

Решение

Воспользовавшись выражением для определения комплексных значений получим:

Комплексные значения полных сопротивлений фаз: Z_ab = 40 Ом, Z_bс = 17,3 + j10 Ом, Z_bс = 8,65 – j5 Ом.

Комплексные и действующие значения линейных и фазных токов:

Дольше можно проводить расчеты, не прибегая к комплексному методу:

Общие активные и реактивные мощности:

Углы сдвига между токами и напряжениями:

Векторная диаграмма для несимметричного треугольника приводилась выше.

🎦 Видео

7. Решение задачи на трехфазные цепи по схеме треугольника.Скачать

Двухфазное КЗ на векторных диаграммахСкачать

Симметричная нагрузка в трехфазной цепиСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Векторная диаграмма токов на комплексной плоскости вручнуюСкачать