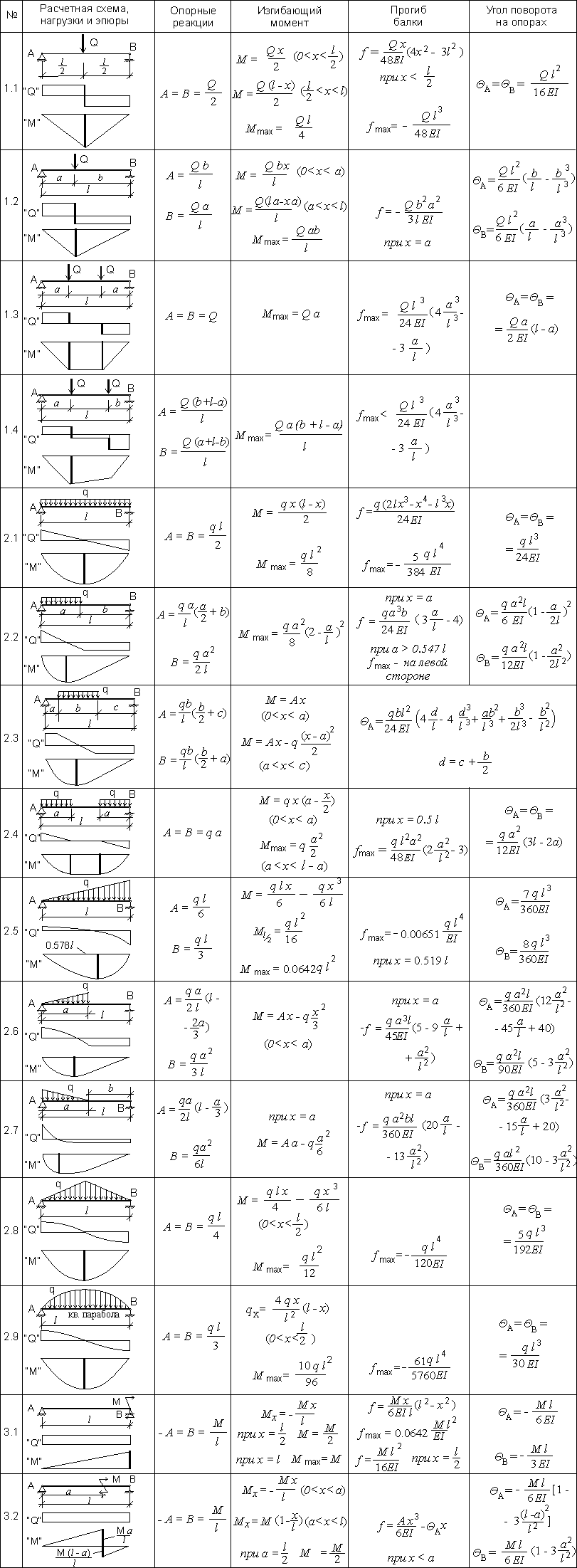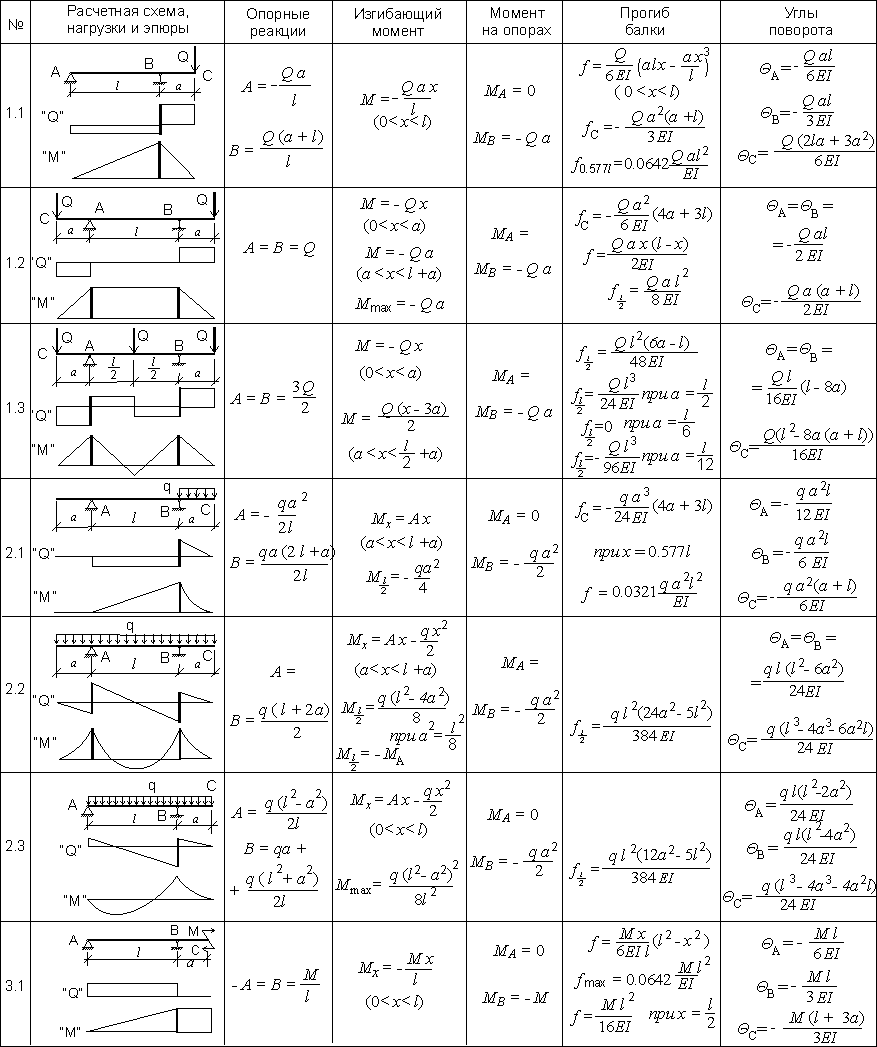Нагрузка на балки треугольником

Расчеты в режиме online

1.5. Треугольная распределенная нагрузка

Построить эпюры поперечных сил и изгиба­ющих моментов для балки, нагруженной распределенной по закону треугольника нагрузкой, если величина максимальной интенсивности нагрузки равна p₀ = 20 кН/м (рис. 1.13).

Решение. Определим опорные реакции балки, для чего заменим распределенную нагрузку сосредоточенной силой Fc, прило­женной в центре тяжести треугольника и равной его площади:

Составим уравнения моментов относительно опор В и D:

Проведем от опоры В на расстоянии х₁ сечение и составим выражения для Q_x и М_х , для чего найдем величину интенсив­ности нагрузки в сечении х₁ . Из подобия треугольников полу­чим:

Заменим треугольную нагрузку на длине х₁ равнодейству­ющей силой F_x, приложенной в центре тяжести треугольника:

I участок: 0 ≤ х₁ ≤ 2,4 м ;

Из уравнений Q_x и М_х следует, что эпюра Q_x представляет квадратичную параболу, а эпюра М_х — кубическую.

Подставив числовые значения x₁ на границах участка, по­лучим

Так как поперечная сила пересекает ось х, найдем коорди­нату поперечного сечения, в котором Q равна нулю, а изгиба­ющий момент имеет максимальное значение:

По вычисленным данным, в соответствии с правилами построения эпюр, строим эпюры Q и M на первом участке.

II участок: 0 ≤ х₂ ≤ 2,4 м ;

Из эпюр следует, что максимальное значение изгибающий момент имеет в сечении, в котором поперечная сила равна ну­лю, М_max = 14,8 кН*м.

Расчетные схемы для балок

Здесь представлены расчетные схемы, различные виды действующих нагрузок, эпюры сил, отображающие характер изменения касательных напряжений, эпюры изгибающих моментов, отображающие характер изменения нормальных напряжений, возникающих в поперечном сечении балки, а также формулы для определения опорных реакций, действующего изгибающего момента, максимального изгибающего момента, формулы для определения прогиба балки на расстоянии х от начала балки и формулы для определения максимального прогиба балки, а также формулы для определения тангенса угла поворота поперечного сечения на опорах и на концах — для консольных балок. Классификация производилась не по действующим нагрузкам, а по виду опор балки. В данном разделе представлены статически определимые балки.

Ось х, относительно которой производятся расчеты изгибающего момента и прогиба, соответствует продольной оси, проходящей через центр тяжести поперечных сечений балки. Значение момента инерции I следует определять относительно оси z (см. сводный сортамент).

Если в таблицах отсутствует формула для определения прогиба на каком-то из участков балки (из-за чрезмерной длины формулы), то опять же ее можно вывести, дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота. Данный метод решения проблемы называется методом начальных параметров.

В общем виде уравнение для определения углов поворота выглядит так:

θ_х = — θ_A + М_Ах/EI + Ax 2 /2EI — qx 3 /6ЕI (173.1)

например, для шарнирной балки, к которой приложена сосредоточенная нагрузка (таблица 1, №1.1, момент и распределенная нагрузка отсутствуют) на участке от начала балки до точки приложения силы (0 2 /2EI = — Ql 2 /16EI + Qx 2 /4EI = Q(4x 2 — l 2 )/16EI (173.2)

Соответственно в общем виде уравнение для определения прогиба выглядит так:

f_х = — θ_Ax + Мх 2 /2EI + Ax 3 /6EI — qx 4 /24ЕI (173.3)

для той же шарнирной балки на участке от начала балки до точки приложения силы (0 3 /6EI = — Ql 2 x/16EI + Qx 3 /12EI = Qx(4x 2 — 3l 2 )/48EI (173.4)

На участке от точки приложения силы до конца балки (l/2 3 /6EI — Q(x — l/2) 3 /6EI (173.5)

Эпюры углов поворота и прогибов поперечного сечения по длине балки не приводятся. Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у.

Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы.

Отдельно приводится пример расчета балки при общем случае загружения несколькими сосредоточенными нагрузками, приложенными несимметрично, по двум вариантам: упрощенному и полному. Сделал я это для наглядности, потому что устал каждый раз объяснять, что не всегда есть большая необходимость в точных расчетах.

Пример расчета балки на сосредоточенную нагрузку, приложенную не посредине пролета (по расчетной схеме 1.2 таблицы 1), с эпюрами сил, моментов, углов поворота и прогибов, также приводится отдельно. Это в общем-то один из самых простых расчетов. С подобного примера и следует начинать. Кроме того в данном примере имеется ссылка на калькулятор, который в случае расчета деревянных балок вообще сам все делает, достаточно ему указать длину пролета, величину нагрузки и расстояние от опоры А до точки приложения нагрузки, ну и длину опорного участка балки (для тех, кто понимает, что это такое).

Пример расчета балки на действие равномерно распределенной нагрузки (по расчетной схеме 2.1 таблицы 1) также имеет место быть, потому как такой расчет — один из самых востребованных при строительстве. К нему также прилагается калькулятор, который пока не онлайн (но со временем все возможно) и его нужно скачивать, что впрочем занимает времени меньше, чем нажимание соответствующих кнопок.

Ссылки на калькуляторы для других случаев загружения балок приводятся отдельно.

Таблица 1. Балка на двух шарнирных опорах.

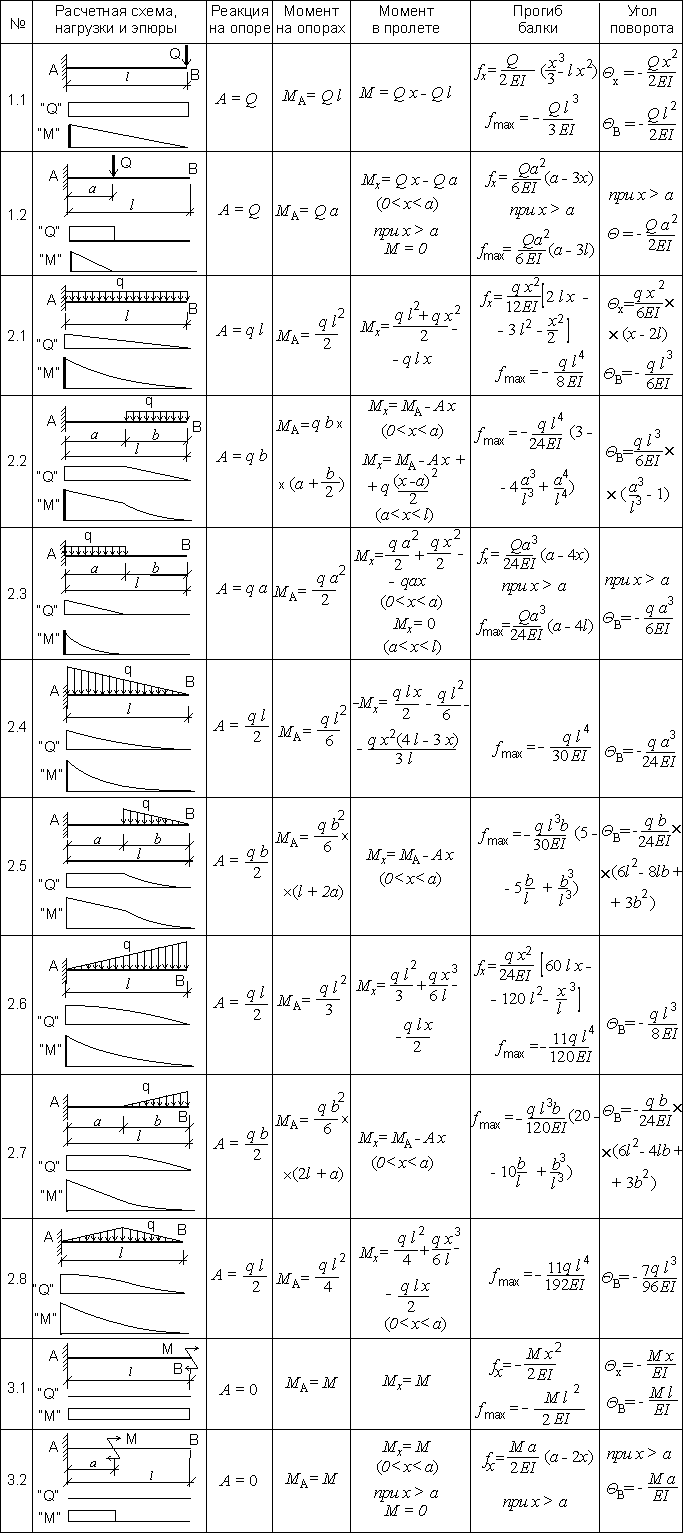
Таблица 2. Консольная балка.

Таблица 3. Балка на шарнирных опорах с консолями.

Так как формулы для балки с консолями различной длины, нагруженной равномерно распределенной нагрузкой, слишком громоздки, то их можно посмотреть в отдельной статье.

Список использованной литературы:

1. Писаренко Г.С. Справочник по сопротивлению материалов. Киев: Наукова думка. — 1988.

2. Фесик С.П. Справочник по сопротивлению материалов. Киев: Будiвельник. — 1982.

3. Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Под ред. Уманского А.А. Москва: Издательство литературы по строительству. — 1972.

Расчетные схемы для статически неопределимых балок представлены отдельно.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Расчетные данные

Оценка пользователей:11.0 (голосов: 16)Переходов на сайт:384777Комментарии:

Допущена опечатка в формуле изгибающего момента для балки с жестким защемлением на опорах(3-я снизу): длина должна быть в квадрате. Допущена опечатка в формуле максимального прогиба для балки с жестким защемлением на опорах (3-я снизу): должно быть без «5».

Да, действительно, были допущены ошибки при редактировании после копирования. На данный момент ошибки исправлены, спасибо за внимательность.

опечатка в формуле в пятом сверху примере (перепутаны степени рядом с иксом и эль)

И это правда. Исправил. Спасибо за внимательность.

В формуле Т.1 2.2 Mmax, похоже, не хватает квадрата после a.

Верно. Эту формулу я скопировал из «Справочника по сопротивлению материалов» (под ред. С.П. Фесика, 1982г, стр. 80) и даже не обратил внимания, что при такой записи даже размерность не соблюдается. Сейчас пересчитал все лично, действительно расстояние «а» будет в квадрате. Таким образом получается, что наборщик пропустил маленькую двоечку, а я повелся на эту пшенку. Исправил. Спасибо за внимательность.

Добрый день хотел бы спросить у вас в таблице 2, схема 2.4, интересует формула «момент в пролете» где не ясен индекс Х -? не могли бы вы ответить)

Для консольных балок таблицы 2 уравнение статического равновесия составлялось слева направо, т.е. началом координат считалась точка на жесткой опоре. Однако если рассматривать зеркальную консольную балку, у которой жесткая опора будет справа, то для такой балки уравнение момента в пролете будет намного проще, например, для 2.4 Мх = qx2/6, точнее -qx2/6, так как сейчас считается, что если эпюра моментов расположена сверху, то момент при этом отрицательный.
С точки зрения сопромата знак момента — достаточно условное понятие, так как в поперечном сечении, для которого определяется изгибающий момент все равно действуют как сжимающие, так и растягивающие напряжения. Главное понимать, что если эпюра расположена сверху, то и растягивающие напряжения будут действовать в верхней части сечения и наоборот.
В таблице минус для моментов на жесткой опоре не проставлен, однако направление действия момента учитывалось при составлении формул.

Скажите пожалуйста, при каком соотношении длины балки к ее диаметру справедливы сии формулы?
Я хочу узнать или это подкодит только для длинных балок, которые в строительстве зданий, или можна применять также для расчета прогибов валов, длиной до 2 м. Пожалуйста ответте так l/D>.

Дмитрий, я вам уже говорил, для вращающихся валов расчетные схемы будут другие. Тем не менее, если вал в неподвижном состоянии, то его можно рассматривать как балку, причем не важно, какое у нее сечение: круглое, квадратное, прямоугольное или какое-то еще. Данные расчетные схемы наиболее точно отражают состояние балки при l/D>10, при соотношении 5

— Спасибо за ответ. Можете еще назвать литературу, на которую я могу сослаться, в своей работе?
Вы имеете в виду, что для вращающихся валов схемы будут другие из-за вращательного момента? Не знаю на сколько это важно, так как в книге по техмашу написано, что в случае токарной обработки, прогиб, вносимый вращательным моментом на валу, очень мал по сравнению с прогибом от радиальной составляющей силы резания. Что думаете?

Не знаю, какую именно задачу вы решаете, и потому вести предметный разговор трудно. Попробую объяснить свою мысль по другому.
Расчет строительных конструкций, деталей машин и т.п., как правило состоит из двух этапов: 1. расчет по предельным состояниям первой группы — так называемый расчет на прочность, 2. расчет по предельным состояниям второй группы. Одним из видов расчета по предельным состояниям второй группы является расчет на прогиб.
В вашем случае на мой взгляд более важным будет расчет на прочность. Более того на сегодняшний день существуют 4 теории прочности и расчет по каждой из этих теорий — разный, но во всех теориях при расчете учитывается влияние как изгибающего так и крутящего момента.
Прогиб при действии крутящего момента происходит в другой плоскости, но все равно при расчетах учитывается. А уж малый этот прогиб или большой — расчет покажет.
Я не специализируюсь на расчетах деталей машин и механизмов и потому авторитетную литературу по этому вопросу указать не смогу. Впрочем, в любом справочнике инженера-конструктора узлов и деталей машин эта тема должна быть должным образом раскрыта.

— Можно тогда с вами пообщаться через mail или Skype? Я вам расскажу что за работу я делаю и для чего были предыдущие вопросы.
mail: dmytro-cx-75@mail.ru
Skype: dmytrocx75

Можете написать мне, адреса электронной почты на сайте найти не трудно. Но сразу предупрежу, никакими расчетами я не занимаюсь и партнерские контракты не подписываю.

Вопрос по таблице 2, вариант 1.1, формула прогиба. Просьба уточнить размерность.
Q — в килограммах.
l — в сантиметрах.
E — в кгс/см2.
I — см4.
Все верно? Что-то странные результаты получаются.

Все верно, на выходе получаются сантиметры.

Здравствуйте. Помогите прикинуть. У нас возле ДК стоит сцена летняя деревянная, размер 12,5 х 5.5 метров, по углам стойки — металлические трубы диаметром 100 мм. Заставляют делать крышу типа фермы (жаль что нельзя рисунок прикрепить) покрытие поликарбонад, фермы изготавливать из профильной трубы (квадрат или прямоугольник) стоит вопрос о моей работе. Не будешь делать уволим. Я говорю что не пойдет, а администрация вместе с моим начальником говорят все пойдет. Как быть?

Рисунок можно добавить на форуме (ссылка на главной странице). А так, без чертежей и знания снеговой нагрузки ничего конкретного сказать не могу.

Если балка (подушка под колонной) лежит на плотном грунте (точнее закопана ниже глубины промерзания), то какой схемой следует воспользоваться для расчета такой балки? Интуиция подсказывает, что вариант «на двух опорах» не подходит и что изгибающий момент должен быть существенно меньше.

Расчет фундаментов — отдельная большая тема. К тому же не совсем понятно о какой балке идет речь. Если имеется в виду подушка под колонну столбчатого фундамента, то основой расчета такой подушки является прочность грунта. Задача подушки — перераспределить нагрузку от колонны на основание. Чем меньше прочность, тем больше площадь подушки. Или чем больше нагрузка, тем больше площадь подушки при той же прочности грунта.
Если речь идет о ростверке, то в зависимости от способа его устойства, он может рассчитываться как балка на двух опорах, или как балка на упругом основании.
Вообще при расчете столбчатых фундаментов следует руководствоваться требованиями СНиП 2.03.01-84.

Имеется в виду подушка под колонну столбчатого фундамента. Длина и ширина подушки уже определены исходя из нагрузки и прочности грунта. Но вот высота подушки и количество арматуры в ней под вопросом. Хотел посчитать по аналогии со статьей «Расчет железобетонной балки», но полагаю, что считать изгибающий момент в подушке, лежащей на грунте, как в балке на двух шарнирных опорах будет не совсем верно. Вопрос — по какой расчетной схеме считать изгибающий момент в подушке.

Высота и сечение арматуры в вашем случае определяются как для консольных балок (по ширине и по длине подушки). Схема 2.1. Только в вашем случае опорная реакция — это нагрузка на колонну, точнее часть нагрузки на колонну, а равномерно распределенная нагрузка — это отпор грунта. Другими словами, указанную расчетную схему нужно перевернуть.
Кроме того, если нагрузка на фундамент передается от внецентренно нагруженной колонны или не только от колонны, то на подушку будет действовать дополнительный момент. При расчетах это следует учитывать.
Но еще раз повторю, не занимайтесь самолечением, руководствуйтесь требованиями указанного СНиПа.

Добрый вечер.Помогите пожалуста,подобрать метал. балку для прольота 4.2 метра.Жилой дом в два етажа,цоколь перекрыт пустотелыми плитами длиной 4.8 метра,сверху несущая стена в 1.5 кирпича длиной в 3.35 м высотой 2.8м.дальше дверной пройом.Сверху на етой стене плиты перекрытия с одной стороны длиной 4.8м. с другой 2.8 метра на плитах опять несущая стена как етажом ниже и сверху деревяные балки 20 на 20см длиной 5м.6 штук и длиной 3 метра 6 штук пол из досок 40мм.25м2. Других нагрузок нету.Прозьба подскозать какую двутавру брать чтобы спать спокойно. Пока всьо ето стоит уже 5 лет.

Посмотрите в разделе: «Расчет металлических конструкций» статью «Расчет металлической перемычки для несущих стен» в ней достаточно подробно описан процесс подбора сечения балки в зависимости от действующей нагрузки.

Подскажите, пожалуйста, где можно ознакомиться с выводом формул максимального прогиба балки для п.п. 1.2-1.4 в Табл.1

Вывод формул для различных вариантов приложения нагрузок на моем сайте не приводится. Общие принципы, на которых основан вывод подобных уравнений, вы можете посмотреть в статьях «Основы сопромата, расчетные формулы» и «Основы сопромата, определение прогиба балки».
Однако в указанных вами случаях (кроме 1.3) максимальный прогиб может быть не посредине балки, потому определение расстояния от начала балки до сечения, где будет максимальный прогиб — отдельная задача. Недавно подобный вопрос обсуждался в теме «Расчетные схемы для статически неопределимых балок», посмотрите там.

допущена ошибка в 2.4 табл 1. не соблюдается даже размерность

Никаких ошибок, а тем более несоблюдения размерности в указанной вами расчетной схеме не вижу. Уточните, в чем именно ошибка.

Добрый день. А у М и Мmax разные единицы измерения?

Таблица 1. Расчет 2.1. Если l возводится в квадрат, значит Мmax будет в кг*м2 ?

Нет, у М и Mmax единая единица измерения кгм или Нм. Так как распределенная нагрузка измеряется в кг/м (или Н/м), то значение момента будет кгм или Нм.

Вечер добрый. Работаю я на производстве мягкой мебели и директор подкинул мне задачку. Прошу вашей помощи, т.к. не хочется решать ее «на глазок».
Суть проблемы такова: в основании дивана планируется металлическая рама из профилированной трубы 40х40 или 40х60, лежащая на двух опорах расстояние между которыми 2200 мм. ВОПРОС: хватит ли сечения профиля при нагрузках от собственного веса дивана + возьмем 3 человека по 100 кг.

Это зависит от множества факторов. К тому же толщину трубы вы не указали. Например, при толщине 2 мм момент сопротивления трубы W = 3.47 см^3. Соответственно максимальный изгибающий момент, который может выдержать труба, M = WR = 3.47×2000 = 6940 кгсм или 69.4 кгм, тогда максимально допустимая нагрузка для 2 труб q = 2х8M/l^2 = 2х8х69.4/2.2^2 = 229.4 кг/м (при шарнирных опорах и без учета крутящего момента, который может возникнуть при передаче нагрузки не по центру тяжести сечения). И это при статической нагрузке, а нагрузка скорее всего будет динамической, а то и ударной (в зависимости от конструкции дивана и активности детей, мои по диванам прыгают так, что дух захватывает), так что считайте сами. Статья «Расчетные значения для прямоугольных профильных труб» вам в помощь.

Док, помогите пожалуйста.
Жестко закрепленная балка, пролет 4 м, опирание по 0,2 м. Нагрузки: распределенная 100 кг/м по балке, плюс распределенная 100 кг/м на участке 0-2 м, плюс сосредоточенная 300 кг посредине (на 2 м). Определил опорные реакции: А – 0,5 т; В – 0,4 т. Дальше я завис: для определения изгибающего момента под сосредоточенной нагрузкой необходимо посчитать сумму моментов всех сил справа и слева от нее. Плюс появляется момент на опорах.
Как считаются нагрузки в этом случае? Надо привести все распределенные нагрузки к сосредоточенным и суммировать (вычесть из опорной реакции * расстояние) согласно формул расчетной схемы? В Вашей статье про фермы раскладка всех сил понятна, а здесь я не могу въехать в методику определения действующих сил.

Для начала, жестко закрепленная балка и опорные участки — понятия несовместимые, посмотрите статью «Виды опор, какую расчетную схему выбрать». Судя по вашему описанию, у вас либо однопролетная шарнирно опертая балка с консолями (см. таблицу 3), либо трехпролетная жестко защемленная балка с 2 дополнительными опорами и не равными пролетами (в этом случае уравнения трех моментов вам в помощь). Но в любом случае опорные реакции при симметричной нагрузке будут одинаковыми.

Я понял. По периметру первого этажа армопояс 200х300h, внешний периметр 4400х4400. В него заанкерено 3 швеллера, с шагом 1 м. Пролет без стоек, на одном из них самый тяжелый вариант, нагрузка несимметричная. Т.Е. считатьбалку как шарнирную?

вообще да. Я так понимаю, что прогиб швеллера провернет и сам армопояс в месте крепления, поэтому получится шарнирная балка?
Максимальный момент посредине, получается M=Q+2q+от несимметричной нагрузки по максимуму 1,125q. Т.е. я сложил все 3 нагрузки, это правильно?

Не совсем так, сначала вы определяете момент от действия сосредоточенной нагрузки, затем момент от равномерно распределенной нагрузки по всей длине балки, затем момент, возникающий при действии равномерно распределенной нагрузки действующей на некотором участке балки. И только затем складываете значения моментов. Для каждой из нагрузок будет своя расчетная схема.

А не ошибка ли в формуле Mmax для случая 2.3 в таблице 3? Балка с консолью, наверно плюс вместо минуса должен быть в скобках

Нет, не ошибка. Нагрузка на консоль уменьшает момент в пролете, а не увеличивает. Впрочем, это видно и по эпюре моментов.

Здравствуйте, во-первых спасибо за формулы, сохранил в закладках. Подскажите, пожалуйста, есть брус над пролетом, на брус ложатся четыре лаги, расстояния: 180мм, 600мм, 600мм, 600мм, 325мм. С эпюрой, изгибающим моментом разобрался, не могу понять как изменится формула прогиба (таблица 1, схема 1,4), если максимальный момент на третьей лаге.

Я уже отвечал несколько раз на подобные вопросы в комментариях к статье «Расчетные схемы для статически неопределимых балок». Но вам повезло, для наглядности я выполнил расчет по данным из вашего вопроса. Посмотрите статью «Общий случай расчета балки на шарнирных опорах при действии нескольких сосредоточенных нагрузок», возможно со временем я ее дополню.

Док, я вообще не могу осилить эти все непонятные для меня формулы. Поэтому прошу у вас помощи. Хочу сделать в доме консольную лестницу (ступеньки из железобетона замуровать при постройке стены). Стена — ширина 20см, кирпич. Длина выступающей ступеньки 1200*300мм Хочу, чтоб ступеньки были правильной формы(не клином). Понимаю интуитивно, что арматура будет «чем-потолще» чтоб ступеньки были чем-потоньше? Но справится ли с железобетон толщиной до 3см нагрузкой в 150кг на краю? Помогите пожалуйста, так не хочется лохануться. Буду очень благодарен, если поможете расчитать.

То, что вы не можете осилить достаточно простые формулы — это ваши проблемы. В разделе «Основы сопромата» все это разжевано достаточно подробно. Здесь же скажу, что ваш проект абсолютно не реален. Во-первых, стена или шириной 25 см или шлакоблочная (впрочем, могу ошибаться). Во-вторых ни кирпичная ни шлакоблочная стена не обеспечат достаточного защемления ступенек при указанной ширине стены. Кроме того, такую стену следует просчитывать на изгибающий момент, возникающий от консольных балок. В-третьих, 3 см — недопустимая толщина для железобетонной конструкции с учетом того что минимальный защитный слой должен составлять в балках не менее 15 мм. И так далее.
Если не готовы все это осилить, то лучше обратитесь к профессиональному проектировщику — дешевле выйдет.

Спасибо за ответ. Буду дальше размышлять. Не судите строго)

что означет х во второй таблице, 2.4

Добрый день! Каку схему (алгоритм) нужно подобрать для расчета балконной плиты, консоль, защемленная с одной стороны, как правильно расчитать моменты на опоре и в пролете?Можно ли ее расчитать как консольную балку, по схемам с таблицы 2, а именно пунктам 1,1 и 2,1. Спасибо!

x во всех таблицах означает расстояние от начала отсчета до исследуемой точки, в которой мы собираемся определить изгибающий момент или другие параметры.

Да вашу балконную плиту, если она сплошная и на нее действуют нагрузки, как в указанных схемах, можно по этим схемам рассчитывать. Для консольных балок максимальный момент всегда на опоре, потому большой необходимости определять момент в пролете нет.

Спасибо большое! Еще хотел уточнить. Я так понял если расчитывать по 2 табл. схема 1.1,(нагрузка приложена на конец консоли) тогда у меня х=L, и соответственно в пролете М=0. Как быть если у меня эта нагрузка еще и по торцам плиты? И по схеме 2.1 я считаю момент на опоре, плюсую его к моменту по схеме 1.1 и по правильному для того что бы заармировать мне нужно найти момент в пролете. Если у меня вылет плиты 1,45м(в свету), как мне расчитать «х» что бы найти момент в пролете?

Момент в пролете будет изменяться от Ql на опоре до 0 в точке приложения нагрузки, что видно по эпюре моментов. Если у вас нагрузка приложена в двух точках на концах плиты, то в этом случае более целесообразно предусмотреть балки, воспринимающие нагрузки по краям. При этом плиту уже можно рассчитывать как балку на двух опорах — балках или плиту с опиранием по 3 сторонам.

Спасибо! По моментам я уже понял. Еще один вопрос. Если балконная плита опираеться с двух сторон, буквой «Г». Катой тогда расчетной схемой нужно пользоваться?

В этом случае у вас будет пластина, защемленная по 2 сторонам и на моем сайте примеров расчета подобной плиты нет.

Уважаемый доктор Лом!
Подскажите, пожалуйста, по какой схеме нужно рассчитать прогиб балки вот такого механизма https://yadi.sk/i/MBmS5g9kgGBbF. Или может быть, не вдаваясь в расчеты, подскажите подойдет ли для стрелы 10 или 12 двутавр, максимальный груз 150-200 кг, высота подъема 4-5 метров. Стойка – труба d=150, поворотный механизм или полуось, или передняя ступица Газели. Укос можно сделать жестким из того же двутавра, а не тросом. Спасибо.

Оценивать надежность подобной конструкции без расчетов не стану, а рассчитать вы ее можете по следующим критериям:
1. Стрелу можно рассматривать как двухпролетную неразрезную балку с консолью. Опорами для этой балки будут не только стойка (это средняя опора), но и узлы крепления троса (крайние опоры). Это статически неопределимая балка, но для упрощения расчетов (что приведет к небольшому повышению запаса прочности) стрелу можно рассматривать как просто однопролетную балку с консолью. Первая опора — узел крепления троса, вторая — стойка. Тогда ваши расчетные схемы 1.1 (для груза — временной нагрузки) и 2.3 (собственный вес стрелы — постоянная нагрузка) в таблице 3. А если груз будет посредине пролета, то 1.1 в таблице 1.
2. При этом нельзя забывать, что временная нагрузка у вас будет не статическая, а как минимум динамическая (см. статью «Расчет на ударные нагрузки»).
3. Для определения усилий в тросе нужно разделить опорную реакцию в месте крепления троса на синус угла между тросом и балкой.
4. Вашу стойку можно рассматривать как металлическую колонну с одной опорой — жестким защемлением внизу (см. статью «Расчет металлических колонн»). К этой колонне нагрузка будет приложена с очень большим эксцентриситетом, если не будет контргруза.
5. Расчет узлов сопряжений стрелы и стойки и прочие тонкости расчета узлов машин и механизмов на данном сайте пока не рассматриваются.

Док, а где Вам можно картинку показать?

Загружаете на любой бесплатный сервис, а здесь указываете адрес страницы с картинкой.

А у Вас вроде еще форум был?

Был, но времени на разгребание спама в поисках нормальных вопросов у меня совершенно нет. Поэтому пока так.

Док, моя ссылка https://yadi.sk/i/GardDCAEh7iuG
какая расчетная схема в итоге получается для балки перекрытия и консольной балки, а также повлияет ли на уменьшение прогиба балки перекрытия (розовая) консольная балка (коричневый цвет)?
стена — пеноблок D500, высота 250 ширина 150, балка армопояса (голубая): 150х300, армирование 2х?12, верх и низ, дополнительно низ в пролете окна и верха в местах опирания балки на проем окна – сетки ?5, ячейка 50. В углах бетонные колонны 200х200, пролет балки армопояса 4000 без стен.
перекрытие: швеллер 8П (розовый), для расчета брал 8У, вварен и заанкерен с арматурой балки армопояса, забетонирован, от низа балки до швеллера 190 мм, от верха 30, пролет 4050.
слева от консоли – проем для лестницы, опирание швеллера на трубу ?50 (зеленая), пролет до балки 800.
справа от консоли (желтый) – санузел (душ, туалет) 2000х1000, пол – заливка армированной ребристой поперечной плиты, габариты 2000х1000 высота 40 – 100 на несъемной опалубке (профлист, волна 60) + плитка на клее, стены –гипсокартон на профилях. Остальной пол- доска 25, фанера, линолеум.
В точках стрелок опирание стоек бака с водой, 200л.
Стены 2 этажа: обшивка доской 25 с двух сторон, с утеплителем, высота 2000, опирание на армопояс.
крыша: стропила –треугольная арка с затяжкой, вдоль балки перекрытия, с шагом 1000, опирание на стены.
консоль: швеллер 8П, пролет 995, сварена с арматурой с усилением, забетонирована в балку, приварена к швеллеру перекрытия. пролет справа и слева по балке перекрытия – 2005.
Пока варю арматурный каркас, есть возможность сдвинуть консоль вправо-влево, но влево вроде не за чем?

Выбор расчетной схемы будет зависеть от того, чего вы хотите: простоты и надежности или приближения к реальной работе конструкции путем последовательных приближений.
В первом случае балку перекрытия можно рассматривать как шарнирно опертую двухпролетную балку с промежуточной опорой — трубой, а швеллер, который вы называете консольной балкой, вообще не учитывать. Вот собственно и весь расчет.
Далее, чтобы просто перейти к балке с жестким защемлением на крайних опорах, следует сначала рассчитать армопояс на действие крутящего момента и определить угол поворота поперечного сечения армопояса с учетом нагрузки от стен 2 этажа и деформаций материала стен под действием крутящего момента. И таким образом рассчитывать двухпролетную балку с учетом этих деформаций.
Кроме того в этом случае следует учесть возможную просадку опоры — трубы, так как она опирается не на фундамент, а на ж/б плиту (как я понял из рисунка) и эта плита будет деформироваться. Да и сама труба будет испытывать деформацию сжатия.
Во втором случае, если вы хотите учесть возможную работу коричневого швеллера, вам следует рассматривать его как дополнительную опору для балки перекрытия и таким образом сначала рассчитывать 3пролетную балку (опорная реакция на дополнительной опоре и будет нагрузкой на консольную балку), затем определять величину прогиба на конце консольной балки, пересчитывать основную балку с учетом просадки опоры и кроме всего прочего также учитывать угол поворота и прогиб армопояса в месте крепления коричневого швеллера. И это еще далеко не все.

Док, спасибо.Мне нужны простота и надежность. Этот участок-самый нагруженный. Я подумывал даже о том, чтобы завязать стойку бака на затяжку стропил, для снижения нагрузки на перекрытие, учитывая, что на зиму вода будет сливаться. В такие дебри расчетов мне не залезть. В общем случае консоль будет снижать прогиб?

Док, еще вопрос. консоль получается в середине пролета окна, имеет ли смысл смещение к краю? С уважением

В общем случае консоль будет снижать прогиб, но как я уже говорил на сколько сильно в вашем случае — большой вопрос, да и смещение к центру оконного проема будет уменьшать роль консоли. И еще, если это у вас самый нагруженный участок, то может быть просто усилить балку, например еще одним таким же швеллером? Я ваших нагрузок не знаю, но нагрузка от 100 кг воды и половины веса бака не кажется мне такой уж внушительной, а вот швеллера 8П с точки зрения прогиба при 4 м пролете проходят ли с учетом динамической нагрузки при ходьбе?

Док, спасибо за добрый совет. После выходных пересчитаю балку как двухпролетную на шарнирах. Если будет большая динамика при ходьбе, я конструктивно закладываю возможность уменьшения шага балок перекрытия. Домик дачный, поэтому динамика терпима. Большее влияние оказывает поперечное смещение швеллеров, но это лечится установкой поперечных связей или креплением настила. Единственно, не посыпется ли бетонная заливка? предполагаю её опору на верхнюю и нижнюю полки швеллера плюс сварная арматура в ребрах и сетка поверху.
Для расчета консоли и установки лучше взять половину пролета от стойки до балки (4050-800-50=3200/2=1600-40/2=1580) или от края окна (1275-40=1235. Да и нагрузку на балку как оконное перекрытие придется пересчитать, но у Вас есть такие примеры. Единсвенное, нагрузку брать как приложенную на балку сверху? Будет ли перераспределение нагрузки, приложенной почти по оси баки?

Я вам уже говорил, на консоль рассчитывать не стоит.
Вы предполагаете опирание плит перекрытия на нижнюю полку швеллера, но как быть с другой стороной? В вашем случае двутавр был бы более приемлемым вариантом (или по 2 швеллера как балка перекрытия).

Док, я понял.
С другой стороной проблем нет-уголок на закладных в теле балки. С расчетом двухпролетной балки с разными пролетами и разными нагрузками пока не справился, попробую перештудировать Вашу статью по расчету многопролетной балки методом моментов.

Добрый день. Хотелось бы у Вас по интересоваться: отливали фундамент: сваи из бетона глубиной 1.8м, а потом отливали бетоном ленту глубиной 1м. Вопрос вот в чем: нагрузка передаётся только на сваи или она равномерно распределяется и на сваи и на ленту?

Как правило сваи делаются при слабых грунтах, чтобы нагрузка на основание передавалась через сваи, поэтому ростверки по сваям рассчитываются, как балки на опорах-сваях. Тем не менее, если вы заливали ростверк по уплотненному грунту, то часть нагрузки будет передаваться основанию через ростверк. В этом случае ростверк рассматривается как балка, лежащая на упругом основании, и представляет собой обычный ленточный фундамент. Примерно так.

Спасибо. Просто на участке получается смесь глины, песка. Причём слой глины очень твёрдый: слой можно снять только при помощи лома и т.д.,т.п.

Я всех ваших условий не знаю (расстояние между сваями, этажность и пр.). По вашему описанию получается, что вы сделали обычный ленточный фундамент и сваи для надежности. Поэтому вам достаточно определить, достаточно ли будет ширины фундамента для передачи нагрузки от дома основанию.

Здравствуйте! Нужна Ваша помощь в расчете. Металлическая воротина 1,5 х1,5 м весом 70 кг крепится на металлической трубе, забетонированной на глубину 1,2 м и обложенной кирпичом (столб 38 на 38 см).Какого сечения и толщины должна быть труба, чтобы не было изгиба?
Я рассчитал по табл. 2, п. 1.1. (http://doctorlom.com/item173.html#comments) как прогиб консольной балки с нагрузкой 70 кг, плечом 1,8 м, труба квадратная 120х120х4 мм, моментом инерции 417 см4. У меня получился прогиб – 1,6 мм? Верно или нет?

Вы правильно предположили, что вашу стойку следует рассматривать, как консольную балку. И даже с расчетной схемой вы почти угадали. Дело в том, что на вашу трубу будут действовать 2 силы (на верхнем и нижнем навесе) и значение этих сил будет зависеть от расстояния между навесами. Больше подробностей в статье «Определение вырывающего усилия (почему дюбель не держится в стене)». Таким образом в вашем случае следует выполнить 2 расчета прогиба по расчетной схеме 1.2, а затем полученные результаты сложить с учетом знаков (проще говоря из одного значения вычесть другое).
P.S. А точность расчетов я не проверяю, тут уж только на себя надейтесь.

Спасибо за ответ. Т.е. мною расчет сделан по максимуму с большим запасом, и вновь рассчитанная величина прогиба всяко будет меньше?

Подскажите, пожалуйста, на схеме 2.2 таблицы 3 как определить прогиб в точке C, если длины консольных участков различны?

В этом случае вам нужно пройти полный цикл. Есть ли в этом необходимость или нет, я не знаю. Для примера посмотрите статью, посвященную расчету балки на действие нескольких равномерно сосредоточенных нагрузок (ссылка на статью перед таблицами).

К моему вопросу от 05 июля 2015г. Есть ли какое правило минимальной величины защемления в бетоне данной металлической консольной балки 120х120х4 мм с воротиной 70 кг.- (например, не менее 1/3 длины)

Вообще-то расчет защемления — отдельная большая тема. Дело в том, что сопротивление бетона сжатию — это одно, а деформации грунта, на который давит бетон фундамента — это совсем другое. Если коротко, то чем больше длина профиля и чем больше площадь, контактирующего с грунтом, тем лучше.

Спасибо! В моем случае металлическая стойка ворот будет заливаться в бетонной свае диаметром 300 мм длиной 1 м., а сваи по верху будут соединены бетонным ростверком с арматурным каркасом? бетон везде М 300. Т.е. деформации грунта не будет. Хотелось бы знать приблизительное, пусть с большим запасом прочности, соотношение.

Тогда действительно 1/3 длины для создания жесткого защемления должно хватить. Посмотрите для примера статью «Виды опор, какую расчетную схему выбрать».

Здраствуйте,как рассчитать балку на двух шарнирных опорах с консолей, участвует сосредоточенная сила и распределенная?

Можно сначала рассчитать балку отдельно на каждую нагрузку по представленным здесь расчетным схемах, а затем полученные результаты сложить с учетом знаков.
Можно сразу составлять уравнения статического равновесия системы и решать эти уравнения.

Здравствуйте, доктор )))
У меня балка по схеме 2.3. В Вашей таблице дана формула для расчета прогиба в середине пролета l/2, а по какой формуле можно просчитать прогиб на конце консоли? Прогиб в середине пролета будет максимальным? Сравнивать с предельно допустимым прогибом по СНиПу «Нагрузки и воздействия» полученный по этой формуле результат надо используя величину l — расстояние между точками А и В? Заранее спасибо, я что-то запуталась совсем. И еще, не могу найти первоисточник, из которого взяты эти таблицы — можно ли название указать?

Как я понял, вы ведете речь о балке из таблицы 3. Для такой балки максимальный прогиб будет не посредине пролета, а ближе к опоре А. В целом величина прогиба и расстояние х (до точки максимального прогиба) зависят от длины консоли, поэтому в вашем случае следует воспользоваться уравнениями начальных параметров, приведенных в начале статьи. Максимальный прогиб в пролете будет в точке, где угол поворота наклонного сечения равен нулю. Если консоль достаточно длинная, то прогиб на конце консоли может быть даже больше, чем в пролете.
Когда вы сравниваете полученный результат прогиба в пролете со СНиПовкским, то длина пролета — это расстояние l между А и В. Для консоли вместо l принимается расстояние 2а (двойной вылет консоли).
Данные таблицы я составил сам, воспользовавшись различными справочниками по теории сопротивления материалов, проверяя при этом данные на предмет возможных опечаток, а также общими методами расчета балок, когда необходимые на мой взгляд схемы в справочниках отсутствовали, поэтому первоисточников много.

Почитал комментарии. Терпения тебе автор, крепкого терпения.

Огромное спасибо Вам за ваши разъяснения. Предстоит куча работ по своему дому. Беседки, навесы, опоры. Попробую вспомнить то что в свое время старательной проспал а потом случайно сдал во Сов.ВТУЗ-е.

А разве не в СИ все размерности? (см коммент 08-06-2013 от Виталия)

Какие именно вы будете использовать единицы кгс или Ньютоны, кгс/см^2 или Паскали, не имеет принципиального значения. В итоге вы все равно получите на выходе сантиметры (или метры). См коммент 09-06-2013 от Доктора Лома.

Здравствуйте у меня балка по схеме 1.4. какая формула для нахождения поперечной силы

Для каждого участка балки значения поперечной силы будут разные (что впрочем видно по соответствующей эпюре поперечных сил). На первом участке 0

Спасибо огромное, вы большой молодец!

Во время наткнулся на ваш сайт. Чуть не промахнулся с расчетами всегда думал что консольная балка с нагрузкой на конце балки будет прогибаться сильнее чем с равномерно распределенной нагрузкой а формулы 1.1 и 2.1 в таблице 2 показывают обратное. Спасибо за вашу работу

Вообще-то сравнивать сосредоточенную нагрузку с равномерно распределенной имеет смысл лишь тогда когда одна нагрузка приведена к другой. Например при Q = ql формула определения прогиба по расчетной схеме 1.1 примет вид f = ql^4/3EI, т.е. прогиб будет в 8/3 = 2.67 раза больше, чем при просто равномерно распределенной нагрузке. Так что формулы для расчетных схем 1.1 и 2.1 ничего обратного не показывают и изначально вы были правы.

добрый день! вот все-таки никак не могу взять в толк-буду очень признателен, если поможете раз и навсегда разобраться-при расчете (любом) обычной балки двутавровой с обычной распределенной нагрузкой по длине какой момент инерции использовать — Iy или Iz и почему? ни в одном учебнике сопромата не могу найти-всюду пишут, что сечение должно стремиться к квадрату и брать надо наименьший момент инерции. Никак не могу ухватить за хвост физический смысл-можно это как-то на пальцах истрактовать?

Я вам советую для начала посмотреть статьи «Основы сопромата» и «К расчету гибких стержней на действие сжимающей внецентренной нагрузки», там все достаточно подробно и наглядно разъяснено. Здесь же добавлю, что мне кажется, вы путаете расчеты на поперечный и продольный изгиб. Т.е. когда нагрузка перпендикулярна нейтральной оси стержня, то определяется прогиб (поперечный изгиб), когда нагрузка параллельна нейтральной оси балки, то определяется устойчивость, другими словами, влияние продольного изгиба на несущую способность стержня. Конечно же при расчетах на поперечную нагрузку (вертикальную нагрузку для горизонтальной балки) момент инерции следует принимать в зависимости от того, какое положение имеет балка, но в любом случае это будет Iz. А при расчетах на устойчивость, при условии, что нагрузка приложена по центру тяжести сечения, рассматривается наименьший момент инерции, так как вероятность потери устойчивости именно в этой плоскости значительно больше.

Здравствуйте, такой вопрос почему в таблице 1 для формул 1.3 и 1.4 формулы прогиба по сути одинаковые и размер b. в формуле 1.4 ни как не отражен?

При несимметричной нагрузке формула прогиба для расчетной схемы 1.4 будет достаточно громоздкой, но при этом следует помнить, что прогиб в любом случае будет меньше, чем при приложении симметричной нагрузки (конечно же при условии b

в таблице 1 для формул 1.3 и 1.4 формулы прогиба вместо Qa^3/24EI должно быть Ql^3/24EI. Долго не мог понять почему прогиб с кристаллом не сходится

Все верно, еще одна опечатка из-за невнимательного редактирования (надеюсь, что последняя, но не факт). Исправил, спасибо за внимательность.

Здравствуйте, Доктор Лом. Вопрос следующий: просматривал фото со стройки и заметил одну вещь: Жб заводская перемычка 30*30 см примерно, оперта на трехслойную жб панель сантиметров на 7. (жб панель немного подпилили для опирания на нее перемычки). Проем под балконную раму 1,3 м, по верху перемычки армопояс и плиты перекрытия чердака. Критичны ли эти 7 см, опирание другого конца перемычки больше 30 см, все стоит нормально несколько лет уже

Если есть еще и армопояс, то нагрузка на перемычку может значительно снизиться. Думаю, все будет нормально и там даже при 7 см достаточно большой запас по прочности на опорной площадке. Но вообще нужно конечно же считать.

Доктор, а если предположить, ну чисто теоретически
что арматура в армопоясе над балкой полностью разрушена, армопояс треснет и ляжет на балку вместе с плитами перекрытия? Хватит ли этих 7 см опорной площадки?

Думаю, даже в этом случае ничего не случится. Но повторю, для более точного ответа нужен расчет.

В таблице 1 в формуле 2.3 для вычисления прогиба вместо «q» указана «Q». Формула 2.1 для вычисления прогиба, являясь частным случаем формулы 2.3, при вобставлении воответствующих значений (a=c=l, b=0) приобретает другой вид.

Все верно была опечатка, но теперь это не имеет значения. Формулу прогиба для такой расчетной схемы я брал из справочника Фесика С.П., как наиболее короткую для частного случая х = а. Но как вы правильно подметили — эта формула не проходит проверки на граничные условия, поэтому я ее вообще убрал. Оставил только формулу для определения начального угла поворота, чтобы упростить определение прогиба по методу начальных параметров.

Подскажите где найти формулу максимального прогиба для двухпролетной шарнирно опертой балки с равномерно распределенной нагрузкой. У вас в табличках что то не нашел

Двухпролетная балка является статически неопределимой. Ссылка на расчетные схемы таких балок в конце статьи.

Здравствуйте. Подскажите, есть здание с ребристым монолитным перекрытием, второстепенная балка шестипролетная. Мне её считать как 6-ти пролетную или можно как 3-ех пролетную

Я всех ваших условий не знаю, поэтому полагаю, что надежнее считать как 6-ти пролетную.

Доктор, чтобы подобрать арматуру, мне её нужно рассчитать от различных комбинаций нагрузки (временная нагрузка в нечетных пролетах, в четных, в 1,2 и4 и т.д), но нашел я максимум для 5-ти пролетной балки. Не знаете ли вы где можно найти для моего случая или самому придется подбирать

В учебных пособиях, насколько я знаю, такой частный случай не рассматривается. Тут поможет только программное обеспечение, например, Лира.

Добрый день в формуле прогиба 1.4 в первой таблице — значение в скобках всегда получаетсья отрицательным

Все правильно, во всех приведенных формулах отрицательный знак в формуле прогиба означает, что балка прогибается вниз по оси у.

Добрый день, доктор лом. Не могли бы Вы написать статейку про крутящий момент в металлической балке — когда он вообще возникает, при каких расчётных схемах, ну и, конечно же, расчёт хотелось бы от Вас увидеть с примерами. У меня — мет балка шарнирно опёртая, один край консольный и на него приходит сосредоточенная нагрузка, а по всей балке распределённая от ж.б. тонкой плиты 100 мм и стены ограждения. Эта балка крайняя. С ж.б. плитой соединяется приваренными к балке с шагом 600 мм стержнями 6 мм. Не могу понять будет ли там крутящий момент, если да — то как его найти и рассчитать сечение балки в связи с ним?

Вообще-то на сайте есть целый раздел, посвященный крутящему моменту, когда он возникает и как его учесть. Раздел так и называется «Крутящий момент».

Спасибо огромное, что подсказали. Уже «бегу» смотреть указанный раздел.

Доброго времени суток «Доктор Лом»! Хочу построить гараж с внутренним размером в плане 9х9 метров в чистоте. Хочу перекрытие выполнить из двутавровых балок, по ним дощатый настил + пароизоляция + утеплитель базалит 150 мм. Крыша будет из профнастила по деревянным стропилам. Не в службу а в дружбу не могли ли Вы мне посоветовать какой двутавр нужен,сколько и с каким шагом между ними?
С уважением Виктор. Приморский край, город Дальнегорск.

Виктор, эмоциональные поглаживания — это конечно хорошо, но их на хлеб не намажешь и семью ими не прокормишь. Для ответа на ваш вопрос требуются расчеты, расчеты — это время, а время — это не эмоциональные поглаживания.

В таблице 2, пример №1.1 ошибка в формуле для тэта(икс)

Здравствуйте, уважаемый доктор у меня вопрос по методу начальных параметров. В начале статьи, у вас написано, что формулу прогиба балки можно получить — дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота.
Допустим я не знаю прогиб балки расчетной схемы 2.1 (табл. 1) . Я дважды проинтегрирую изгибающий момент ?q*l2/8dx=q*l3/24;?q*l3/24dx=q*l4/96.
После разделю значение на EI. q*l4/(96*EI).
И прибавлю к нему результат интегрирования угла поворота это — ?q*l3/24dx=q*l4/96. q*l4/(96*EI)+q*l4/(96*EI)=q*l4/(48*EI).
У вас получается значение -5*q*l4/(384*EI).
Подскажите пожалуйста. Где я допустил ошибку?

Ошибка в том, что вы проинтегрировали не уравнение моментов, а результат решения этого уравнения для точки посредине балки, а это разные вещи. Кроме того при сложении следует внимательно следить за знаком «+» или «-«. Если вы внимательно проанализируете формулу прогиба, приводимую для данной расчетной схемы, то поймете о чем речь. А еще при интегрировании угла поворота результат q*l4/48, а не q*l4/96 и в окончательной формуле он будет идти с минусом, так как такой начальный угол поворота будет приводить к прогибу балку ниже оси х.

Приветствую, в Т.1 2.3 формулы для моментов что принимается за X? Середина распределенной нагрузки?

Для всех таблиц, расстояние х — это расстояние от точки начала координат (как правило опора А) до рассматриваемой точки на нейтральной оси балки. Т.е. приведенные формулы позволяют определить значение момента для любого поперечного сечения балки.

Оплатил билет на вход- 100 руб. Жду приглашения, -для расчёта консольной балки миниатюрной формы из кварцевой пластины. Владимир Мостяев. 8-916-121-28-36

Владимир, я отправил вам письмо.

Добрый день. В формулах прогиба однопролетной балки с одной и двумя консолями под равномерно распределенной нагрузкой у вас перепутаны знаки в скобках. Для балки с двумя консолями у вас стоит (24а^2 — 5L^2) должно быть наоборот (5L^2 — 24a^2). Во второй формуле та же ошибка.

Александр, это не ошибка. Если вы внимательно читали вводную часть, то там сказано: «Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у». Просто иногда бывают случаи (опять же в случаях с консольной балкой), когда рассматриваемое сечение действительно имеет положительный прогиб (например конец консоли поднимается вверх) и об этом следует помнить. Впрочем кому как удобнее, на окончательный результат это никак не влияет.

Вводную часть я вообще не читал, мне ни к чему. Но я вас понял. Просто, я как-то не подумал, что запись формул может отличаться от тех, которым меня учили 40 лет назад. Я привык,видеть прогиб направленный вниз, как положительное число и наоборот отрицательное, если вверх. У Отрешко, Мичурина, Дыховичного формулы прогиба представлены именно так, вниз — положительная величина, вверх — отрицательная. Поэтому у Отрешко формула прогиба консольной балки записана, как (5 — 24a^2/l^2)*ql^4/384EI. Прошу прощения за недопонимание.

Александр, размышления на тему нашей переписки я изложил в отдельной статье «Формула прогиба». Здесь же скажу лишь то, что у меня формулы прогиба записаны именно так, как они выглядят после надлежащего интегрирования уравнений изгибающих моментов.

Это понятно, чем вы руководствовались делая такую запись. Балка прогибается вниз, в декартовой системе координат прогиб относительно оси х идет вниз и получает отрицательную величину по оси у. У вас так и записано. Загвоздка тут в другом. В той же системе координат мы рисуем моменты изгиба, но. Но направленный вниз момент мы пишем с положительным знаком и это общепринятая практика. Вот и получается по вашим формулам, например, для однопролетной балки вы записываете момент изгиба нарисованный вниз со знаком плюс, а прогиб со знаком минус. Получается дисбаланс. В одной и той же системе координат записываются разные знаки. Если бы мы рисовали моменты на сжатых волокнах (как буржуины) то запись прогиба со знаком минус не вызвала бы вопросов, но мы рисуем их на растянутых волокнах и пишем при этом «плюс». Вот это меня и зацепило, когда искал готовую формулу прогиба для нужной мне балки. Как-то привык, что вниз это плюс, вверх — минус. В наших картинках эпюра моментов практически повторяет линию прогибов, на консолях только нужно проявлять воображение.

Здравствуйте! Для схемы 2.3, табл.1, какая формула макс.изг.момента?

Для схемы 2.3 нужно сначала определять сечение, в котором касательные напряжения равны нулю по формуле: А — q(x — a) = 0.

Скажите пожалуйста у меня пролет 5,5 метра. Балка 6,30 метра, диаметр арматуры 16мм , снизу 3 и сверху 3 арматуры по длину поставили и залили бетоном. Ширина балки 40 см а высота 45 см получилось. На него 30 рядов керпича хотим укладывать выдержит ли это балка. Заранее спасибо

Вы не указали класс бетона и арматуры, но все равно предполагаю, что выдержит с большим запасом. Больше подробностей смотрите в статье «Определение несущей способности железобетонной балки».

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Расчёт балки на прогиб и прочность

Скачать, сохранить результат

Выберите способ сохранения

Информация

Балка занимает роль основополагающего элемента в несущей конструкции. Её функция приравнивается к стержню всей конструкции, который прочно закрепили. При строительстве какого-либо сооружения очень важно осуществить грамотный расчет балки на прогиб и исключить допущение ошибки в расчетах. Прежде всего расчет требуется для определения того, на сколько балка деформируется в процессе эксплуатации сооружения. Если при расчете показатель деформации находится в пределах нормы, то можно определить нужные показатели будущей балки (сечение, материал, размер и так далее).

Делая расчет балки на прочность, необходимо четко знать виды материала, из которого изготавливаются балки (сталь, дерево, бетон, алюминий, стекло и медь). Далее нужно обратить внимание на то, что типы нагрузок, как и их схемы также различаются. Так, например, распределенная нагрузка означает, что давление оказывается не на одну точку, а распределено по всей площади балки. Сосредоточенный тип нагрузки характеризует направленность давления на один небольшой участок (точку) балки.

Вместе с типами, существуют четыре схемы нагрузок:

• Шарнир-Шарнир
• Заделка-Шарнир
• Заделка-Заделка»
• Свободный конец

Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок, при этом абсолютно исключив вероятность допущения ошибки в процессе расчета. Обычно рассчитывают деревянные балки, а также металлические. В процессе вычисления показателя определяется сумма сил, воздействующих на балку, которые направлены перпендикулярно конструкции. Расчет деревянной балки на прогиб осуществляется с учетом материала, т.е. учитывают вид древесины, её гибкость и многие другие параметры, также важно учесть форму сечения балки и нагрузка какого вида оказывается на балку. Сравнивая с расчетом балки из древесины, расчет металлической балки на прогиб существенно отличается, поскольку важное внимание уделяют виду соединения: электросварка, заклепки, болты и другие виды соединений.

Все перечисленные выше нюансы позволяют понять, что расчет балки на прогиб — крайне ответственный этап в процессе стройки какого-либо объекта. От него зависит надежность, долговечность и целостность всей конструкции. Наш калькулятор позволит Вам быстро и безошибочно провести предельно точный расчет.

Какие преимущества даёт наш калькулятор?

• экономия времени;
• исключение допущения ошибки;
• предельная точность в расчете;
• приятный и понятный интерфейс;
• дополнительный справочный материал.

Таким образом, созданный нами онлайн калькулятор является незаменимым инструментом в процессе работы специалиста, которому необходимо осуществить расчет балки или любого другого важного показателя.

📺 Видео