Творческая работа практическоц направленности с презентацией
- Просмотр содержимого документа «РАбота Вектор»
- Применение векторов в повседневной жизни
- Просмотр содержимого документа «Применение векторов в повседневной жизни»
- Презентация ««Векторы в нашей жизни
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Выберите документ из архива для просмотра:
- Описание презентации по отдельным слайдам:
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔥 Видео
Просмотр содержимого документа
«РАбота Вектор»
Возникновение понятия «вектор»………………………….
Векторы в профессиях
С понятием вектор я познакомилась на уроках геометрии. Особого интереса она у меня не вызвала. Однако, практически сразу понятие «вектор» встретилось и на уроках физики. Тогда стало ясно, что вектор не сугубо математическое понятие, оно применяется и в других областях науки. Вектор — это направленный отрезок. А зачем они нужны? Встречаются ли они в жизни? Может, стоит присмотреться? Если вы начинаете утро с прогноза погоды, то слышали, к примеру: «Ветер северо-западный, скорость 18 метров в секунду». Нельзя не согласится,, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости. Идем в школу: видим дорожные знаки, вроде этих:
Придя в школу или на работу, видим направляющие знаки:
Примеры направляющих знаков вы можете увидеть в Приложении 1. Видим, что векторы присутствуют в нашей жизни.
Актуальность изучения данной темы связано с многообразием сфер применения векторов: от искусства до сложных задач моделирования реальных процессов. Понятие вектора используется во многих приложениях математики, таких, как современная алгебра и геометрия, теория функций и теория вероятностей. Учебники по таким, на первый взгляд, далеким от математики предметам, как электротехника, радиотехника, теория антенн и др., очень широко используют векторы.
Я решила выяснить, в каких именно областях науки применяются векторы, насколько это понятие актуально в жизни.
Целью моей работы:
Рассмотреть векторы как математические модели реальных процессов.
Перед собой я поставила такие задачи:
Изучить литературу по данной теме;
Изучить понятие «вектор» в предметах естественно-научного цикла;
Узнать, как осуществляется моделирование с помощью векторов.
Установить, используется ли данное понятие в жизни;
Возникновение понятия «вектор»
Одним из основных понятий математики являются «вектор». Развитие этого понятия происходило благодаря широкому использованию его в различных областях математики, информатики, механики, а так же в технике.
Вектор – молодое математическое понятие. Этот термин впервые употребил ирландский математик Уильям Гамильтон в 1845 году в своих работах по построению числовых систем, обобщающих комплексные числа. Также он ввел термины «скаляр», «скалярное произведение», «векторное произведение». Исследования в этой области проводил ещё немецкий физик-математик Г.Грассман. Его идеи об абстрактных векторных пространствах привели к важному открытию – возможности рассматривать цветовые ощущения как трехмерные векторы. Это легло в основу современного учения о свете. Им были установлены законы сложения цветов.
Понятие «вектор» стало широко использоваться в математике в XIX веке, когда стал активно развиваться раздел математики «Комплексные числа». Векторы использовались для наглядного представления таких чисел. В школах эта тема изучается с 1963 года. Сейчас понятие вектора стало одним из ведущих понятий школьного курса математики.
Есть такое высказывание: «Карьера начинается в школе», поэтому я решила глубже изучить понятие «вектор», рассмотреть его значение в математическом моделировании и выяснить в каких профессиях применяется данное понятие.
Использование векторов в различных науках:
Векторы — мощный инструмент не только математики, но и физики. Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Многие физические величины, такие, как сила, скорость, ускорение, характеризуются не только числовым значением, но и направлением. Эти величины очень удобно изображать в виде направленных отрезков. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. Векторная алгебра является фундаментом, на котором построена классическая физика. С помощью векторов можно моделировать различные физические процессы. Например, некоторые физические поля (магнитное и электромагнитное, сила тяжести) рассматриваются как векторные поля. Такая модель позволяет применять к изучаемым понятиям удобные методы математических расчётов.
Векторные величины в физике: скорость, перемещение, ускорение, сила, импульс, напряженность электрического поля, магнитная индукция, момент силы. Для этих величин важно «сколько» и «куда».
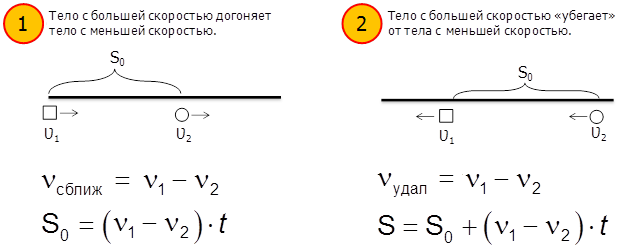
Скорость изучается на уроках математики и на уроках физики, и при решении многих задач на скорость необходимо сделать рисунок, на котором направление движения показывается стрелками. Векторами удобно моделировать движение в одном направлении, в разных направлениях, движение по кругу, движение по воде. Составленная таким образом схема-модель поможет решить задачу.
Пример схем некоторых задач на движение:
Тело с большей скоростью догоняет тело с меньшей скоростью:
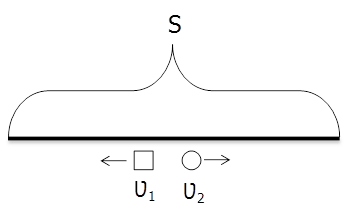
Движение в противоположные стороны:
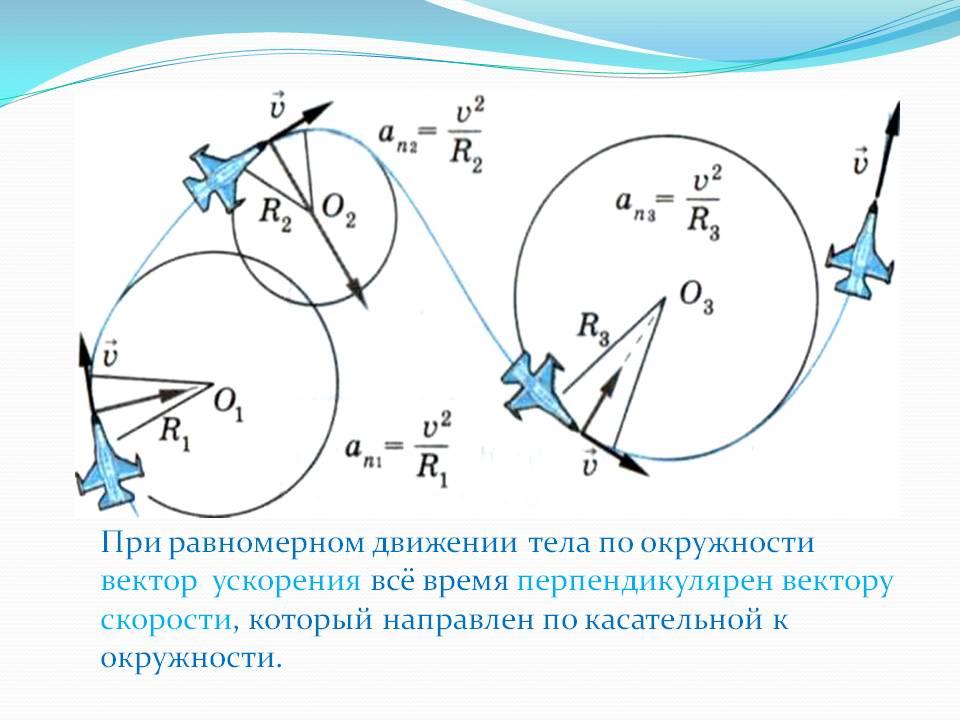
Равномерным движением по окружности называется такое движение, при котором скорость не меняется по модулю, а меняется лишь её направление. При этом вектор ускорения перпендикулярен вектору скорости. Вектор скорости направлен по касательной к окружности.
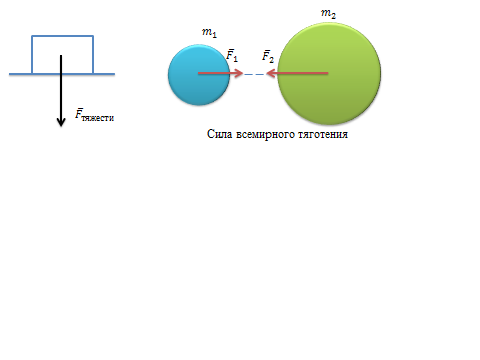
Еще одна физическая векторная величина, которую я хотела бы рассмотреть – это сила. Сила определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Результат действия силы зависит от направления. На рисунке вы можете видеть модель направления силы тяжести и всемирного тяготения.
В физике можно найти ещё много примеров, где векторы применяются как средство моделирования физических процессов.
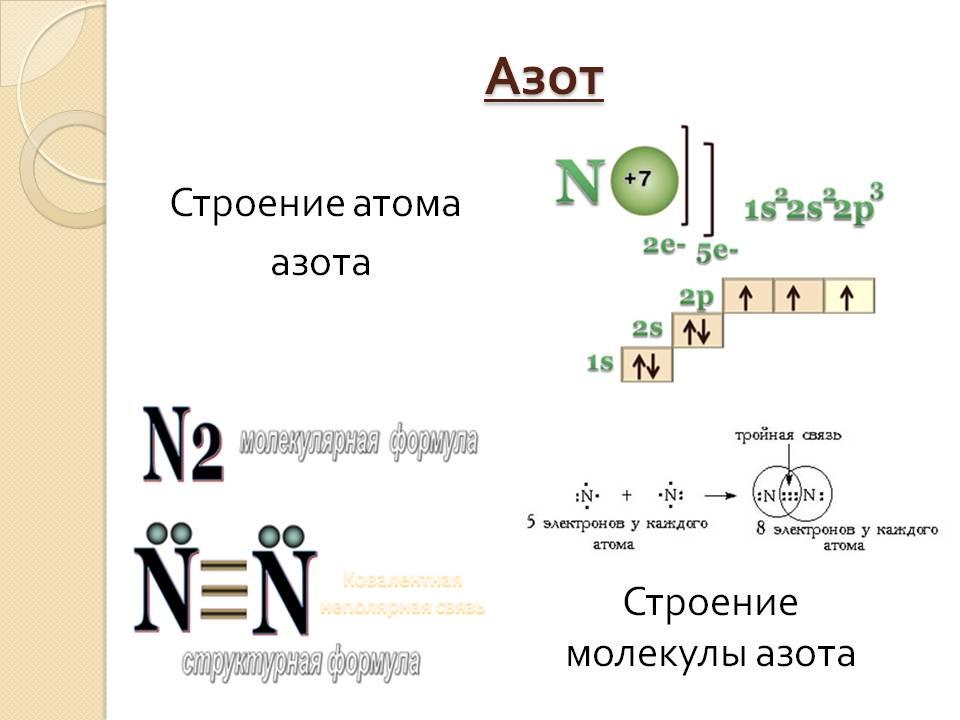
Также векторы помогают создавать математические модели некоторых химических процессов. Например, для того, чтобы показать строение атома используются всё те же векторы.
На схеме вы можете видеть строение атома азота:
На таких схемах стрелками изображается электрон, а направление соответствует направлению спина (собственного магнитного момента электрона). Операции над спинами производятся так же, как и операции над векторами, что позволяет трактовать химические процессы языком математики. Примером векторных частиц, имеющих спин служат: фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний.
Химические реакции записываются с помощью уравнений, в записи которых используются векторы.
Пример, реакция обмена, взаимодействие хлорида кальция и нитрата серебра с образованием осадка хлорида серебра:
CaCl2( ж ) + 2AgNO3( ж ) 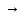
Биология относится к наукам естественно-математического цикла. Часто для того, чтобы смоделировать тот или иной процесс, приходится использовать язык математики или переносить суть математических понятий на понятия биологические. Суть понятия «вектор» — это направленность. В биологии этим словом называют организм, который переносит паразита от одного организма к другому. Например, клещи являются переносчиками вируса, вызывающего энцефалит. В генетике вектором считается молекула нуклеиновой кислоты, которая используется для передачи генетического материала другой клетке. С помощью организмов векторов синтезируются различные лекарственные средства, в том числе и антибиотики, ферменты, необходимые человеку (инсулин).
В настоящее время создана векторная модель для доставки в клетки костного мозга гена, кодирующего гранулоцитарный колониестимулирующий фактор человека. Данный белок относится увеличивает продолжительность жизни клеток костного мозга, усиливает функциональную активность зрелых нейтрофилов. Созданный вектор представляет собой многослойную конструкцию. Эффективность описанной векторной модели была доказана опытным путем. При конструировании противовирусных вакцин немаловажное значение имеет создание специального вектора-носителя, обеспечивающего адресную доставку генов и их защиту от действия нуклеаз крови.
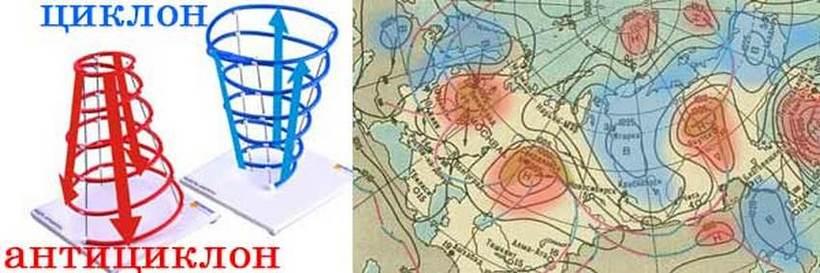
Оказывается, векторы, как отрезки, показывающие направление нашли своё отражение и в географии. Так, ветер – характеризуемый величиной и направлением, рассматривается как вектор. Распределение ветра исследуется в векторной форме. Таким образом, ветер (горизонтальное движение воздушных частиц относительно подстилающей поверхности) – векторная величина и описывается двумя параметрами – скоростью ( м/с) и направлением. Вектор – модель ветра. Аналогично, с помощью векторов показывают направление движения воздушных масс в циклонах и антициклонах.
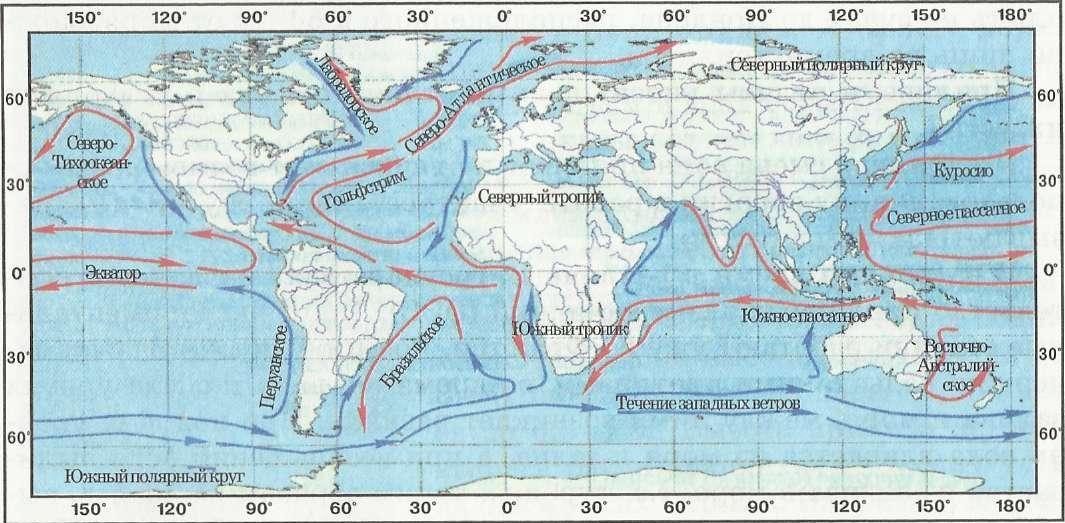
Вектор также служит моделью всевозможных течений. Горизонтальные перемещения водных масс в морях и океанах называются морскими течениями. К элементам, характеризующим течение, относятся направление и скорость. Значит, течение – векторная величина. С помощью векторов и действий над ними осуществляется учет приливно-отливных течений.
Течение реки, подводные течения океанов показывают с помощью векторов.
С помощью векторов составляют карты миграции птиц и животных.
Используя действия над векторами можно рассчитать пролетные пути перелетных птиц.
Векторы в профессиях.
Я выяснила, что векторы используются во многих науках для моделирования самых различных процессов и явлений. Значит, это понятие потребуется во всех технических профессиях, профессиях, связанных с компьютерном деле, в медицине, химии и т.д. Векторы нужны для освоения профессии строителя и архитектора, так как особое место вектору отводится в сопромате, ведь нагрузка на разные элементы конструкций является разложением вектора по базису векторов силы тяжести и других приложенных к конструкции сил. В самолетостроении, судостроении, автомобилестроении при конструировании транспорта также применяются векторы и их свойства.
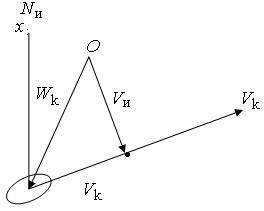
В науке судовождение используются векторы и их свойства для определения кажущегося ветра во время движения судна. В штилевую погоду на судне, имеющего ход, всегда ощущается встречный ветер, равный скорости судна. Он имеет название курсовой ветер и имеет направление, противоположное движению судна. Таким образом, на движущемся судне наблюдается кажущийся ветер, вектор которого равен геометрической сумме истинного и курсового ветров. Для определения направления ветра используется способ построения векторного треугольника.
Векторы понадобятся и портному для правильного составления выкроек одежды.
Выполнив работу, я увидела, что векторы находят широкое применение в геометрии и в прикладных науках, где используются для представления величин, имеющих направление (силы, скорости и т. п.).
Вектор может служить моделью для любого явления, характеризующегося величиной и направлением. Так, в физике – это сила, ускорение, скорость; в химии – это изображения строения атома, изображения химических реакций; в биологии – это модель переноса вирусов, процессов клонирования и создания вакцин; в географии – это модель ветра, течения. Таким образом, векторное исчисление является универсальным инструментом, позволяющим создавать математические модели физических, химических и биологических процессов. Векторы широко используются в экономике и компьютерной графике, при построении вычислительных нейронных структур и всем известных популярных социальных сетей. Умение оперировать с объектами посредством векторного исчисления помогает находить удобные и наглядные пути решения сложных задач, поэтому хорошее знание этого раздела школьной математики необходимо каждому, чья будущая профессия связана с техникой, компьютерами, естественными науками, пространственным мышлением.
Башмаков М.А. Что такое вектор?-2-е изд., стер.- М.: Квант, 1976.-221с.
Выгодский М.Я. Справочник по элементарной математике.-3-е изд., стер. — М.: Наука, 1978.-186с.
Гусятников П.Б. Векторная алгебра в примерах и задачах.-2-е изд., стер.- М.: Высшая школа, 1985.-302с.
В.В. Элементарная математика. Повторительный курс.-3-е изд., стер.- М.: Наука,1976.-156с.
Коксетер Г.С. Новые встречи с геометрией.-2-е изд., стер. — М.: Наука,1978.-324с.
Погорелов А.В. Аналитическая геометрия.- 3-е изд., стер. — М.: Квант,1968.-235с.
Видео:All Vector Tricks IN REAL LIFE (Parkour Game)Скачать

Применение векторов в повседневной жизни
С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.
Просмотр содержимого документа
«Применение векторов в повседневной жизни»
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.
Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.
Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.
История возникновения понятия вектор
Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]
Векторы в математике
Вектором называется направленный отрезок, который имеет начало и конец.[1]




Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.
Операции над векторами




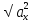
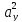
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

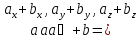

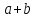


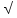
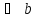
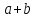
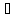

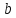
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же 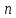
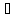

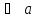
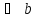
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:




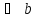
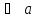
Умножение вектора на число


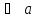

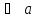
Скалярное произведение векторовСкалярное
Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними. 
Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии
Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.
Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».
Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.
Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
Векторы в экономике
Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.
Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
Векторы в психологии
На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.
Векторы в повседневной жизни
Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.
Векторы в знаках дорожного движения
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.
Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.
Каждый человек постоянно сталкивается с векторами в повседневной жизни.
Векторы необходимы нам для изучения не только математики, но и других наук.
Видео:(Вектор в реальной жизни) #1Скачать

Презентация ««Векторы в нашей жизни
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Обучение Трюкам Из Вектора В Реальной Жизни | Паркур Трюки VectorСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Презентация по теме Векторы в нашей Жизни.pptx
Описание презентации по отдельным слайдам:
Векторы в нашей жизни
Векторы в физике Векторы напряженности электрического поля
Векторы в строительстве Любая сила, например F тяжести, раскладывается по векторам. Это необходимо при расчётах в строительстве различных сооружений, например в построении моста, через реку.
Векторы в химии Электронное строение атома азота . Каждый электрон имеет свою собственную характеристику – спин. Спин – собственный момент импульса электрона, не связанный с движением в пространстве. Спины электронов складываются как векторы.
Векторы в биологии Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому.
Векторы в медицине Вектор- бактериальная плазмида. Плазмиды дают бактериям большие преимущества, например способность синтезировать вещества опасные для других бактерий – антибиотики, а так же быть устойчивыми к антибиотикам своих собратьев. С помощью векторов синтезируются различные лекарства и антибиотики.
Векторы вокруг нас Ель можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора
Баннеры, вывески, знаки дорожного движения
Краткое описание документа:
Данная презентация представляет собой обобщение и систематизацию материала из различных областей знаний, использующих в качестве объекта исследования понятие «Вектор». Материал можно применять на уроке-обобщения по теме «Векторы в пространстве», геометрия, 10 класс.На мой взгляд, презентация способствует развитию познавательного интереса и способствует формированию положительной мотивации к изучению достаточно сложного для обучающихся предмету — геометрии.Важно показать, что геометрия, хоть и сложна, но очень важна в нашей жизни.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 933 человека из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 316 человек из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 696 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Видео:Вектор - В реальной жизни. №1Скачать

Дистанционные курсы для педагогов
Другие материалы
- 01.04.2014
- 811
- 01.04.2014
- 1160
- 01.04.2014
- 2964
- 01.04.2014
- 3159
- 01.04.2014
- 695
- 01.04.2014
- 661
- 01.04.2014
- 6066
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
Настоящий материал опубликован пользователем Косачёва Марина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На проекте: 7 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 25881
- Всего материалов: 4
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Обучение Трюкам Из Вектора В Реальной Жизни | Паркур Трюки VectorСкачать

Дистанционные курсы
для педагогов
530 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Пандемия позволила детям получить больше внимания со стороны родителей
Время чтения: 1 минута
В Китае приняли закон о сокращении нагрузки на школьников
Время чтения: 1 минута
Порядка 65% выпускников российских вузов идут работать по специальности
Время чтения: 1 минута
В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔥 Видео
VECTOR ПАРКУР ТРЮКИ В РЕАЛЬНОЙ ЖИЗНИСкачать

All Vector tricks in real life (parkour game) - паркур трюки из игры ВекторСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Некоторые вырезанные трюки из Vector 2Скачать

Бросили Вызов Крутому Паркурщику! **БАБЛ КВАС В Реальной Жизни**Скачать

Обучение Трюкам Из Вектора В Реальной Жизни | Паркур Трюки VectorСкачать

ГОЛОВОЛОМКА в Реальной Жизни !Скачать

VECTOR ЛЕГКИЕ ПАРКУР ТРЮКИ ИЗ ВЕКТОРА В РЕАЛЬНОЙ ЖИЗНИСкачать

vector in real life | вектор в реальной жизниСкачать

😱 ОГО! Майнкрафт в *РЕАЛЬНОЙ ЖИЗНИ*!Скачать

КАК ИСПОЛЬЗОВАТЬ вектора в реальной ЖИЗНИСкачать

ВЕКТОР - ТРЮКИ В РЕАЛЬНОЙ ЖИЗНИСкачать

Вектор В Реальной Жизни | Паркур Трюки Из Вектора VectorСкачать

ВЕКТОР 2 - ТРЮКИ В РЕАЛЬНОЙ ЖИЗНИСкачать

Vector ALL TRICKS In Real Life (Parkour game)Скачать