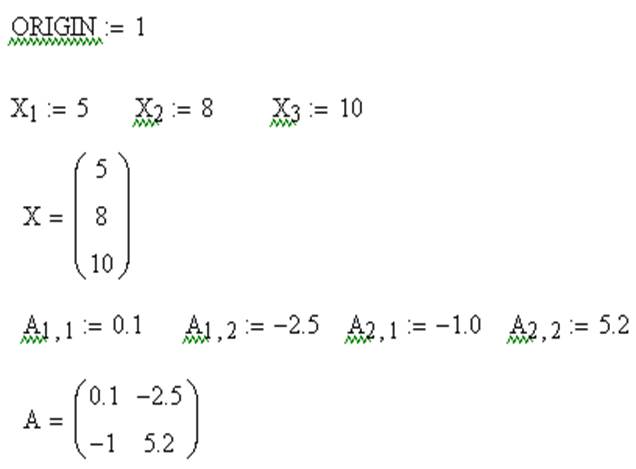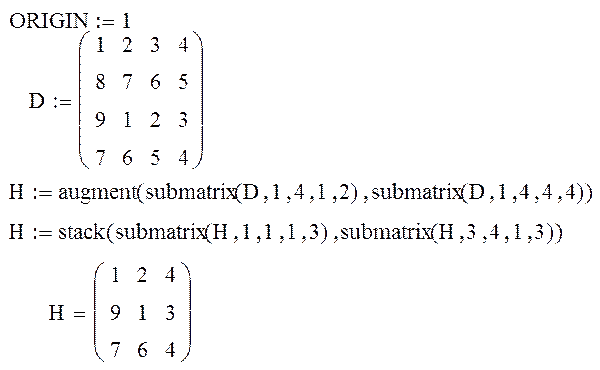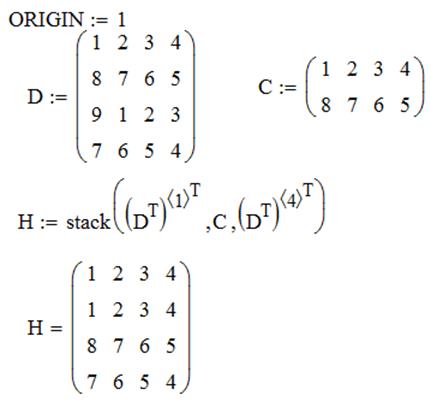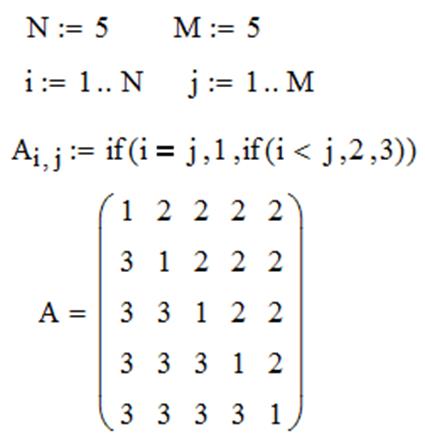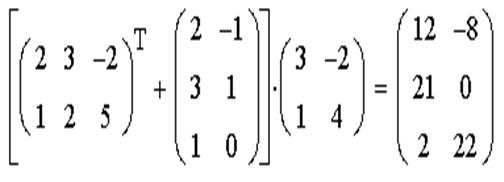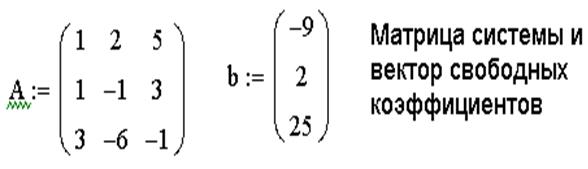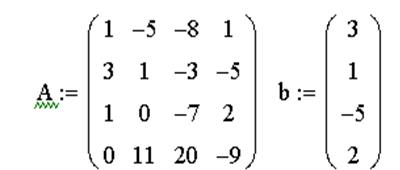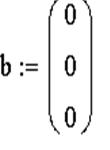Вектор средних значений матрицы (6 видео)

Найти средний вектор матрицы

Для заданной матрицы размером M x N задача состоит в том, чтобы найти средний вектор данной матрицы.

Примеры:

Подходить:
Давайте возьмем матричный мат размером 5 × 3, представляющий длину, ширину, высоту 5 объектов.
Теперь результирующий средний вектор будет вектором строки следующего формата:

Примечание: если у нас есть матрица измерения M x N , то результирующий вектор строки будет иметь размерность 1 x N
Теперь просто вычислите среднее значение каждого столбца матрицы, которое даст требуемый средний вектор.

// C ++ программа для поиска среднего вектора
// данной матрицы
#include

using namespace std;

#define rows 3
#define cols 3

// Функция поиска среднего вектора

void meanVector( int mat[rows][cols])

// цикл для обхода каждого столбца

for ( int i = 0; i

// рассчитать среднее значение каждой строки

Содержание

Как работает метод главных компонент (PCA) на простом примере
Шаг 1. Подготовка данных
Шаг 2. Ковариационная матрица
Шаг 3. Собственные вектора и значения (айгенпары)
Шаг 4. Снижение размерности (проекция)
Шаг 5. Восстановление данных
Вместо заключения – проверка алгоритма
Векторы и матрицы в MathCAD
📽️ Видео

Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

Как работает метод главных компонент (PCA) на простом примере

В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.

Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.

В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.

К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.

Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.

Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.

Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.

Шаг 1. Подготовка данных

Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.

В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!

Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер (точнее, разброс).

Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.

Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.

Шаг 2. Ковариационная матрица

В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!

Для описания формы случайного вектора необходима ковариационная матрица.

Это матрица, у которой (i,j)-элемент является корреляцией признаков (X_i, X_j). Вспомним формулу ковариации:

В нашем случае она упрощается, так как

и это справедливо для любых случайных величин.

Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.

Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.

И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).

Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии X_i и X_j, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)

Шаг 3. Собственные вектора и значения (айгенпары)

О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X₁ и X₂), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.

Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.

Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна v T X. Дисперсия проекции на вектор будет соответственно равна Var(v T X). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:

Соответственно, дисперсия проекции:

Легко заметить, что дисперсия максимизируется при максимальном значении v T Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:

Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).

Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.

Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии.

И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.

Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.

В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.

На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т.е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.

Шаг 4. Снижение размерности (проекция)

Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.

Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).

Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!

Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.

Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию v T X (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора v T берем матрицу базисных векторов V T . Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.

dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)

Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.

Шаг 5. Восстановление данных

С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.

Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выборки: X T v T +m

Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.

Вместо заключения – проверка алгоритма

Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.

Параметр n_components указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:

Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.

В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.

Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:

— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_

Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!

Сравним полученные нами значения со значениями библиотечной функции.

Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.

Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).

Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.

Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Векторы и матрицы в MathCAD

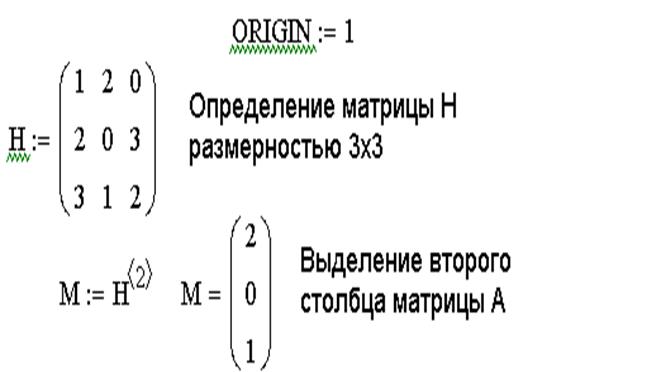
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.

Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.

Поэлементный ввод массива Х

Вводимые символы	Отображаемые символы
X [ 1 Shift+: 5	X₁:=5
X [ 2 Shift+: 8	X₂:= 8
X [ 3 Shift+: 10	X₃:= 10

Поэлементный ввод матрицы А

Вводимые символы	Отображаемые символы
A [ 1,1 Shift+: 0.1	A₁₁ := 0.1
A [ 1,2 Shift+: -2.5	A₁₂ := -2.5
A [ 2,1 Shift+: -1.0	A₂₁ := -1.0
A [ 2,2 Shift+: 5.2	A₂₂ := 5.2

Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке в панели математических инструментов.

ПанельMatrix содержит следующие кнопки:

– определение размеров матрицы;

– ввод элемента массива ;

– вычисление матрицы, обратной к данной ;

– вычисление определителя матрицы ;

– оператор векторизации (поэлементные операции с векторами и матрицами) ;

– определение столбца матрицы ;

– транспонирование матрицы ;

– определение ранжированной переменной;

– вычисление скалярного произведения векторов;

– вычисление векторного произведения векторов;

– вычисление суммы компонент вектора.

– визуализация цифровой информации.

Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки панели Matrix:

1. Ввести с клавиатуры имя матрицы и знак присваивания;

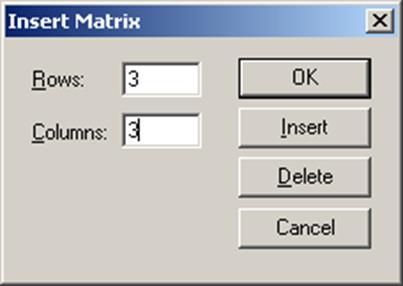
2. Щелчком по кнопке открыть окно диалога:

3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;

4. Закрыть окно диалога, щелкнув по кнопке OK;

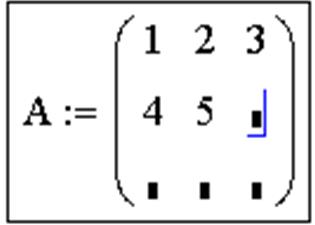
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:

Функции определения матриц и операции с блоками матриц:

matrix(m,n,f) – создает и заполняет матрицу A=<a_ij> размерности m на n, каждый элемент которой a_ij равен значению функции f(i,j);

diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

identity(n) – создает единичную матрицу порядка n;

augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);

stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);

submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l

Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;

Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;

Функции вычисления различных числовых характеристик матриц:

last(v) – вычисление номера последнего элемента вектора v;

length(v) – вычисление количества элементов вектора v;

rows(A) – вычисление числа строк в матрице А;

cols(A) – вычисление числа столбцов в матрице А;

max(A) – вычисление наибольшего элемента в матрице (векторе) А;

min(A) – вычисление наименьшего элемента в матрице (векторе) А;

mean(A) – вычисление среднего значения матрицы (вектора) А;

tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;

ranc(A) – вычисление ранга матрицы А;

Функции, реализующие численные алгоритмы:

rref(A) – приведение матрицы А к ступенчатому виду;

geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;

lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.

lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;

qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;

cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;

sort(v) – сортировка элементов вектора v в порядке возрастания их значений;

reverse(v) – перестановка элементов вектора v в обратном порядке;

csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;

rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.

ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.

ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.

ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.

ЗАДАЧА 4. Элементы матрицы формируются по формуле 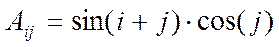. Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.

ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:

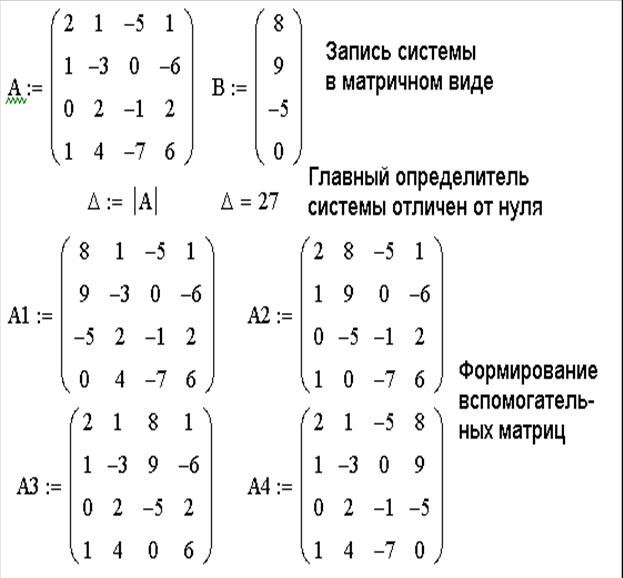
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:

Для решения поставленной задачи необходимо выполнить следующие действия:

1. Сформировать матрицу системы А и вектор правых частей b.

2. Вычислить главный определитель ∆.

3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆_i;

4. Вычислить определители ∆_i;

5. Найти решение системы по формуле x_i=∆_i/∆.

ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.

1. Сформировать матрицу коэффициентов и вектор свободных членов системы.

2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.

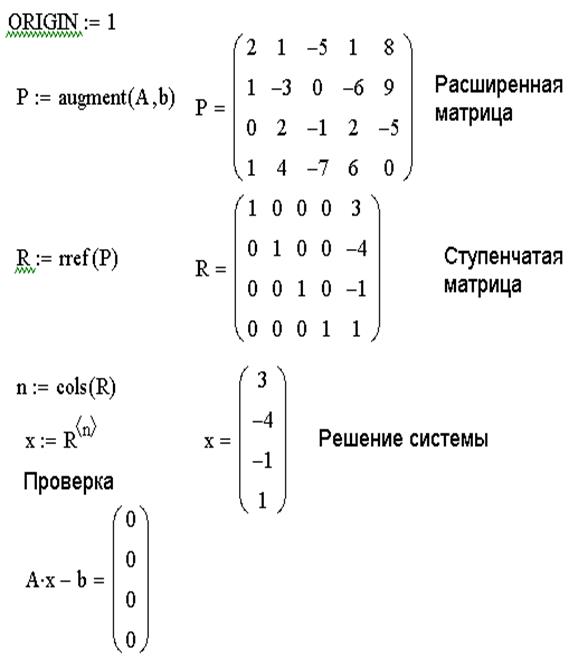
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.

Порядок решения задачи:

1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.

2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);

3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.

4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.

5. Выполнить проверку Ax-B=0.

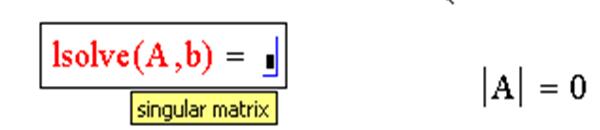
ЗАДАЧА 9. Решить систему при помощи функции lsolve:

Пример системы, которая не имеет решений:

Пример системы, которая имеет бесконечное множество решений

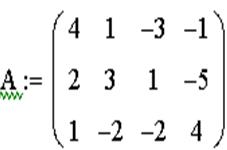
ЗАДАЧА 10. Решить систему при помощи решающего блока.

Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.

Правее и ниже ключевого слова записываются уравнения системы.

Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.

Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.

Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).

Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).