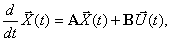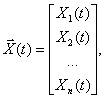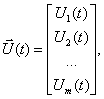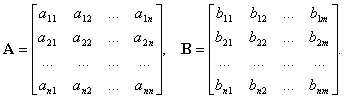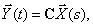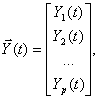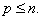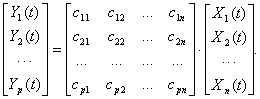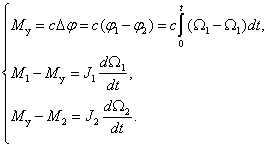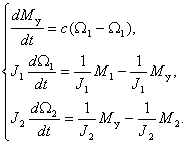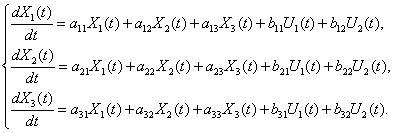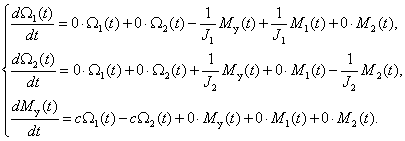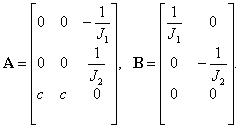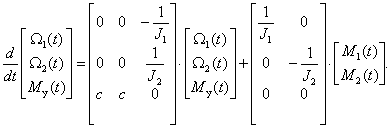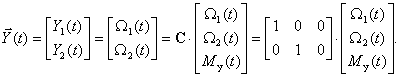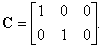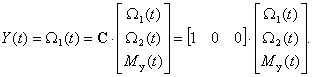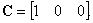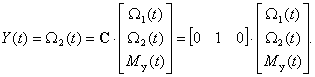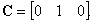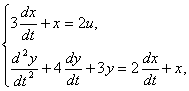Вектор состояния и вектор наблюдения (8 видео)

Вектор состояния и вектор наблюдения

Математические модели в пространстве состояний

Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид

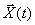
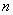
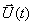
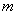
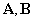
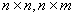
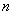
где вектор состояния размерности , который включает в себя переменные объекта, однозначно определяющие его состояние,

вектор управления или входа размерности , который включает в себя сигналы, действующие на систему извне,

матрицы параметров, включающие в себя параметры системы, размерность которых соответственно ,

порядок системы.

Иногда уравнение состояния (1) записывают в развернутой форме

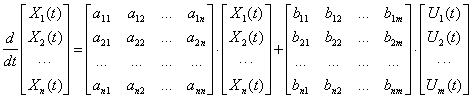
Уравнение состояния и структура полностью описывают объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.

Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы)

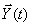
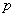
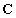
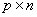
где вектор выхода размерности , который содержит переменные объекта, доступные для наблюдения,

матрица параметров размерности

в системах управления

Уравнение выхода (2) также можно записать в развернутой форме

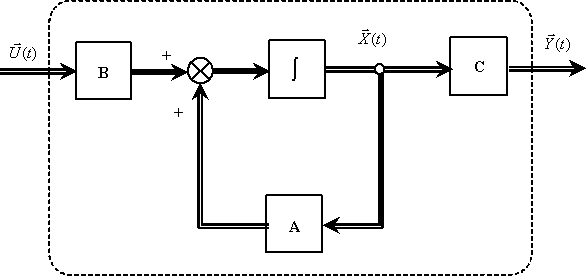
Графически уравнение состояния и уравнение выхода могут быть представлены в виде, показанном на рис. 1.

Символ интегрирования на схеме означает покомпонентное интегрирование векторной величины.

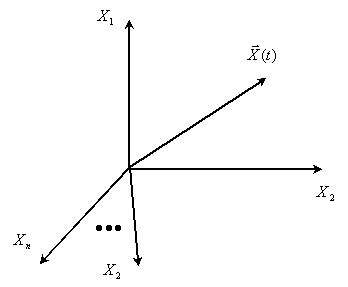
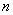
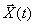
В общем виде пространство состояний мерной системы задается радиус-вектором в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.

Рассмотрим несколько примеров представления процессов в пространстве состояний.

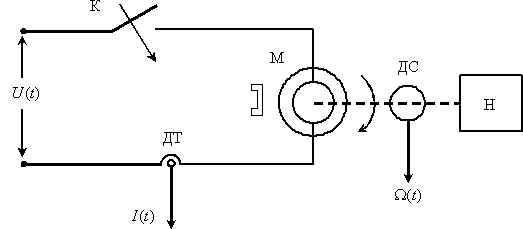
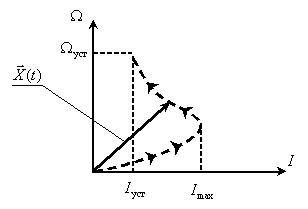
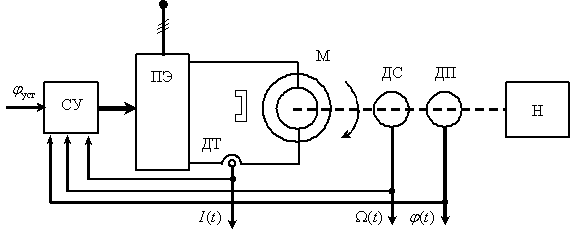
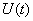
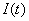
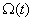
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 3. Пуск производится подключением с помощью контакта (К) напряжения , при этом в цепи будет протекать ток и двигатель будет вращать вал с нагрузкой (Н) со скоростью , ток и скорость определяются с помощью датчиков соответственно ДТ ДС.

Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задаем в следующем виде

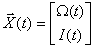
Вектор входа будет иметь только одну компоненту 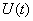. Графики изменения во времени переменных двигателя показаны на рис. 4.

На рис. 4 введены обозначения: 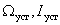установившиеся значения соответственно скорости и тока, максимальное значение тока при пуске.

Сформируем двухмерное пространство состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.

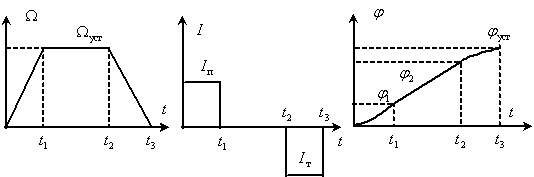
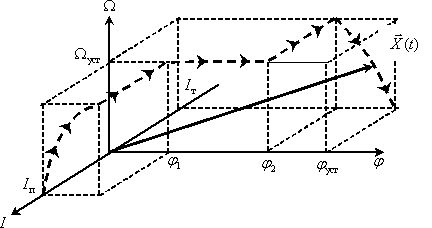
Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение , в автоматизированном электроприводе, показанном на рис. 6.

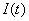
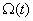
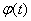
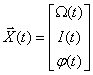
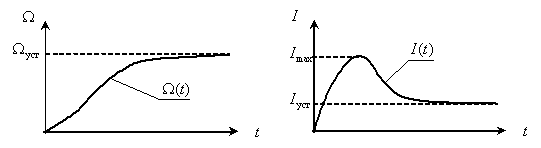
В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменные двигателя ток , скорость и положение вала

Графики изменения во времени переменных двигателя показаны на рис. 7.

Сформируем трехмерное пространство состояний электропривода с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам изменения компонент вектора состояния.

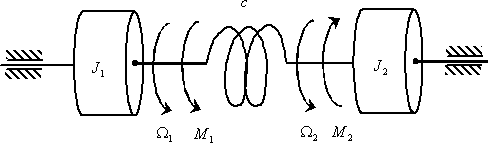
Теперь рассмотрим получения математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 9.

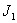
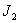
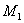
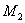
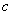
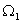
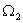
Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции и . К каждой массе прикладывается извне момент ( и ), массы соединены валом, обладающим упругими свойствами (), массы вращаются со скоростями и .

Система дифференциальных уравнений, описывающих систему, имеет вид

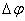
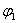
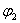
где разность углов положения первой и второй масс.

Так как уравнения состояния (1) и выхода (2) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы мы должны выполнить следующее:

задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,

определить матрицы параметров уравнений.

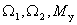
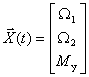
Состояние системы определяется тремя переменными , поэтому задаем вектор состояния следующего вида

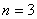
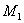
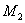
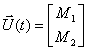
Порядок системы . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это моменты и , поэтому вектор входа имеет вид

Порядок вектора выхода 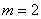. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.

Преобразуем уравнения системы (3) к форме Коши

Нам требуется получить уравнение состояния для системы третьего порядка с вектором входа второго порядка, посмотрим, что представляет собой это уравнение в общем виде

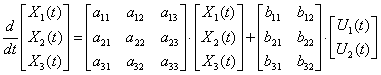
Раскрывая матричные скобки, получим

Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (4) в виду (5), для этого следует:

расположить уравнения в порядке следования компонент в векторе состояния,

расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,

отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.

В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.

Преобразуем систему (4) к виду (5), в результате получим

В результате по коэффициентам слагаемых в правых частях (6) получим искомые матрицы параметров уравнения состояния

Уравнение состояния в развернутом виде

Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианты датчиковых систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):

Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода

То есть имеем ,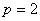

Датчик скорости установлен на первой массе, уравнение выхода

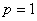
Датчик скорости установлен на второй массе, уравнение выхода

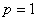
Контрольные вопросы и задачи

Перечислите компоненты уравнения состояния (векторы и матрицы), их размерности.

Поясните смысл уравнения выхода, перечислите компоненты и их размерности.

По системе дифференциальных уравнений, описывающих многомерную систему

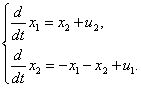
полагая векторы состояния и входа

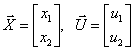
записать уравнение состояния в развернутой форме.

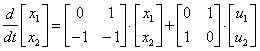
По уравнению состояния

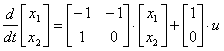
описывающему многомерную систему, определить систему дифференциальных уравнений, связывающих компоненты векторов состояния и входа.

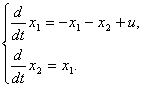
По системе дифференциальных уравнений, описывающих многомерную систему

полагая векторы состояния и входа

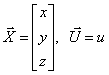
записать уравнение состояния в развернутой форме.

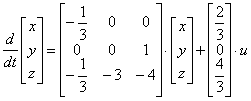
Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

ЛИНЕЙНАЯ СТАЦИОНАРНАЯ ДИНАМИЧЕСКАЯ СИСТЕМА

Пусть динамический объект управления и его измерительный комплекс представляют собой линейную стационарную систему, которая описывается математической моделью в матричном виде:

где А, В, С, D — постоянные матрицы размерности соответственно п х п, п х г, т х п, т х г.

Для проверки на наблюдаемость линейной стационарной системы составляется матрица К

Система считается наблюдаемой, если для нее ранг матрицы К равен п. Для нее существуют такие разрешающие операции, которые ввиду линейности системы (8.4) также являются линейными. Они имеют вид

где V — линейный оператор с элементами v_sh отражающий разрешающие операции (s, i = 1, . п). По существу здесь проводится косвенное измерение параметров состояния путем непосредственного измерения вектора наблюдения у(/) и использования выражения (8.7) с оператором V

Значения элементов линейного оператора и его структура определяются фундаментальной матрицей динамического объекта (8.4) и матрицей С измерительного комплекса (8.5).

Для стационарной системы можно взять любое время для оценки состояния. Для определенности примем, что t = /₀— Так как управляющее воздействие u(t) измеряется и коэффициенты математической модели (8.4) и измерительного комплекса (8.5) известны, можно ограничиться случаем, когда управляющее воздействие отсутствует, т.е. и(/) = 0. В этом случае вектор наблюдения у(/) связан с вектором состояния х(/Ь) линейной зависимостью

где X(t, to) — фундаментальная матрица дифференциального уравнения, которое является моделью динамического объекта (8.4).

Из выражения (8.7) следует, что для определения состояния объекта в начальный момент времени необходимо найти значения элементов оператора V.

Рассмотрим два случая.

1. Пусть размерность векторов состояния и наблюдения одинаковая, т.е. п = т.

В этом случае оператор V легко найти из выражения (8.8) как обратную матрицу произведения двух матриц С и X. Он равен

Этот случай тривиален и не представляет интереса для нахождения оптимального решения.

2. Пусть размерность вектора наблюдения меньше, чем состояния, т.е. т = 0. В результате имеем

Выберем соответствующие компоненты векторов (8.13) таким образом, чтобы объект управления (8.1, 8.2) удовлетворял критерию наблюдаемости. Тогда состояние динамического объекта может быть оценено с помощью выражения

1 — неособая матрица размерности (пх п), составленная из столбцов матрицы (8.6), соответствующих вектору у; у — вектор-строка, состоящая из компонентов векторов (8.13).

Если y(t) — скалярная величина, то выражение (8.14) примет вид

Из выражения (8.15) следует, что при наблюдении динамического объекта (8.1) с помощью скалярной величины y(t) (т = 1) при At = 0 линейный оператор V равен обратной матрице наблюдаемости (8.6). Этот результат интересен тем, что он показывает физический смысл матрицы наблюдаемости.

Таким образом, при оценке состояния динамического объекта могут иметь место различные варианты измерительных комплексов, а также все возможные алгоритмы измерения. В любом случае разрешающие операции отличаются оператором V, поэтому выбор оптимального варианта сводится к анализу его структуры, который можно провести, используя рассмотренный ранее метод выбора оптимального способа измерения.

Найдем компоненты метрического тензора. Для линейной стационарной динамической системы оператор также является линейным. Для него компоненты метрического тензора определяются суммой произведений /-го и к-го его столбцов:

Метрический тензор полностью характеризует метрические свойства линейного динамического объекта (8.1) в координатах вектора наблюдения в заданный момент времени /₀. После его определения для каждого из сравниваемых измерительных комплексов нетрудно найти оптимальный вариант для оценки состояния системы (8.1, 8.2) в момент времени /₀, пользуясь формулами, полученными в п. 7.

В соответствии с выражениями (8.7, 8.10, 8.11) компоненты метрического тензора зависят как от момента времени to, для которого определяется текущее состояние динамической системы, так и от интервала наблюдения АЛ Варьируя этими переменными, можно определить тот момент времени и такой интервал наблюдения, когда текущее состояние динамической системы определяется с максимальной точностью при одном и том же ограничении на ресурсы.

Изложенный ранее подход к выбору оптимального измерительного комплекса можно использовать и в том случае, если текущее состояние необходимо определять в течение всего переходного процесса. При такой постановке задачи необходимо разбить время переходного процесса на ряд промежутков и для каждого провести соответствующие расчеты. Критерий выбора оптимального варианта здесь должен быть интегральным.

Пример. Рассмотрим линейную стационарную систему (8.4), которая характеризуется трехмерным вектором с координатами x_t(t), x₂(t), x₃(t) и матрицей А, равной

Пусть вектор наблюдения (8.5) состоит из двух координат у^/), у₂(0, восстановление вектора состояния также может осуществляться двумя способами, т.е. имеем две матрицы С:

В обоих случаях ранг матрицы К равен трем, и, следовательно, объект полностью наблюдаем.

Найдем линейный оператор V. Фундаментальная матрица для рассматриваемого примера имеет вид

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

ВЕ́КТОР СОСТОЯ́НИЯ

В книжной версии

Том 4. Москва, 2006, стр. 710

Скопировать библиографическую ссылку:

ВЕ́КТОР СОСТОЯ́НИЯ, физическая величина, характеризующая возможное состояние квантовой системы; одно из осн. понятий квантовой механики . В отличие от классич. механики, где движение тел описывается экспериментально измеримыми величинами – наблюдаемыми (координатами, импульсом, моментом импульса, энергией и т. д.), в квантовой механике результаты измерений той или иной величины предсказываются лишь вероятностно. Все возможные состояния данной системы образуют пространство состояний (бесконечномерное гильбертово пространство ), элементами которого и являются В. с. Как и в математике, В. с. можно складывать, получая новые возможные состояния ( суперпозиции принцип ), умножать на комплексные числа, каждой паре В. с. сопоставляется комплексное число – их скалярное произведение.