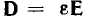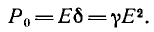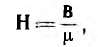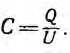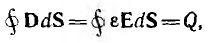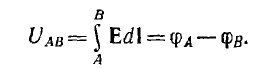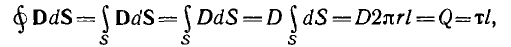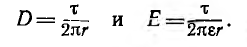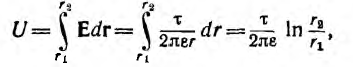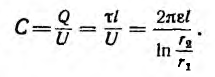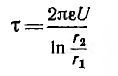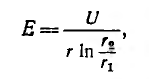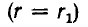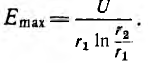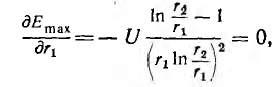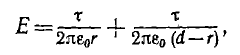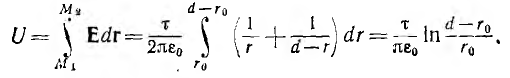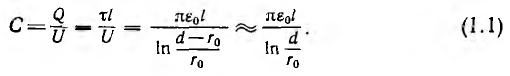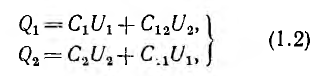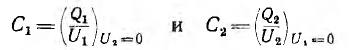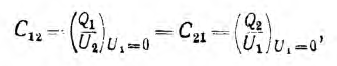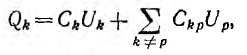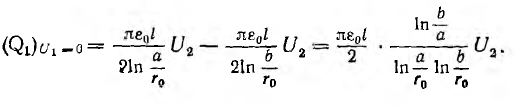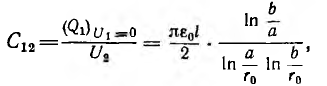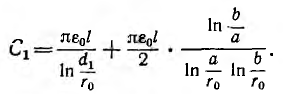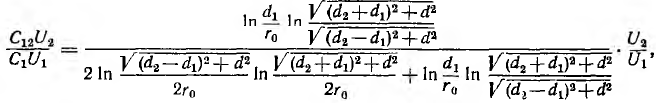Коаксиальный кабель представляет собой два длинных соосных проводящих цилиндра, пространство между которыми заполнено каким-либо изолирующим материалом с магнитной проницаемостью /1. Пусть а — радиус внутреннего цилиндра, а 6 — внешнего. Длина кабеля обычно во много раз превышает его радиус. Поэтому магнитное поле, создаваемое электрическим током в кабеле, будет таким же как у бесконечно длинного кабеля, если не учитывать искажения поля у его концов.
Найдем индуктивность участка кабеля длиной /. Для этого создадим замкнутую электрическую цепь из внутреннего и внешнего цилиндров кабеля и подключим к этой цепи источник постоянной ЭДС (рис. 8.6, а). Токи, создаваемые этой ЭДС, потекут по поверхностям цилиндров вдоль их оси в противоположных направлениях.
Рис. 8.6. Коаксиальный кабель
В силу цилиндрической симметрии системы силовые линии магнитного поля суть семейство окружностей, центры которых лежат на оси симметрии. На рис. 8.6, а изображена одна из силовых линий. Для определения напряженности магнитного поля применим теорему (7.7) о
циркуляции вектора Н . В качестве контура интегрирования С выберем силовую линию произвольного радиуса г. Циркуляция вектора напряженности по такому контуру будет
Если радиус контура С меньше радиуса внутреннего цилиндра (г 6), сумма токов равна нулю, так как токи в цилиндрах имеют противоположные направления. Поэтому напряженность магнитного поля Н = 0 при г 6, т.е. магнитное поле внутри малого цилиндра и вне большого отсутствует. Если радиус контура С таков, что а
Посмотреть оригинал
- Расчёт индуктивности многопроволочных кабельных жил в программной среде ELCUT
- Электрическая ёмкость и ее расчет
- Параметры электрических и магнитных цепей
- Электрическая ёмкость и ее расчет
- Емкость коаксиального кабеля
- Емкость двухпроводной линии
- Взаимоёмкость и ее расчёт
- Взаимоемкость двух параллельных двухпроводных линий
- 🔥 Видео
Коаксиальный кабель
Передача (транспортировка) электрической энергии по коаксиальному кабелю
Коаксиальный кабель
Подключение бесконечно протяженного кабеля без индуктивности и утечки к источнику постоянного напряжения U
0) и его изоляция между проводами очень хорошая (G0
Видео:индуктивность коаксиального кабеляСкачать

Расчёт индуктивности многопроволочных кабельных жил в программной среде ELCUT
Ранее 1,2) были рассчитаны погонные ёмкости триад и витых пар простейших конструкций с учётом эффектов скрутки как однопроволочных жил в сердечниках так и проволок в многопроволочных жилах. Сформулированная же в названии статьи задача несколько сложнее. Это связано с существенной разницей в протекании электрических и электромагнитных процессов в рассматриваемых объектах.
И потому уместно обсудить этот вопрос несколько подробнее.
Ёмкость C – это коэффициент пропорциональности между потенциалом U проводника и его зарядом Q: Q = CU.
Расчёт С для проводников кабелей существенно облегчен рядом обстоятельств.
Во-первых, электрическое поле в проводники практически не проникает, так как заряд электризованных металлов сосредоточен в приповерхностном слое толщиной порядка радиуса дебаевской экранировки
10 28 . 10 29 м -3 – концентрация носителей заряда в металлах, ε – диэлектрическая проницаемость. Этот радиус порядка межатомного расстояний в решётке металла, так что их объёмы практически «выключены» из электростатических процессов. Это существенно облегчает процедуру вычисления различных контурных и поверхностных интегралов.
Во-вторых, время проникновения электрического поля в металлы исчезающе мало: оно порядка εε0 /σ
10 -18 с – максвелловского времени релаксации.
В-третьих, за время Ø/V
100 ГГц; V = 1 мм – диаметр проводника, V
2 10 8 м/с – скорость распространения электромагнитного поля вдоль кабеля) происходит выравнивание U на поверхности провода. Это намного меньше характерной длительности сигналов (иногда это обстоятельство формулируют иначе: длина волны много больше поперечного размера линии связи). Кроме того, ёмкости они не зависят от частоты (если нет частотной зависимости ε).
Так что с помощью указанного выше общепринятого выражения можно практически однозначно определить величины ёмкостных параметров кабельной продукции.
Чего нельзя сказать про погонные индуктивные параметры L проводников, если традиционно понимать их как коэффициенты пропорциональности связывающие поток магнитной индукции Ф вокруг проводника и его ток J:
Или иным математически эквивалентным способом (например, через эдс электромагнитной индукции, энергию магнитного поля: см. ниже). Это связано с тем, что, в отличие от электрического, магнитное поле в проводники проникает, причём на частотах
10 4 1/c почти полностью (µ0 = 4π 10 -7 Гн/м, для меди σ = 5.98 10 7 Сим/м).
Причём из-за скин-эффекта и эффекта близости токи и магнитные поля распределены по сечению проводников неоднородно. Кроме того, время диффузии магнитного поля в проводник 1/ω
10 -4 с соизмеримо со временами сигнальных процессов.
По всем этим причинам выражения типа (1) однозначно определяют индуктивный параметр L только для проводников и токов с особо высокой симметрией (плоской или коаксиальной). И не работают в применении к кабельной продукции с произвольной формой поперечного сечения проводников. В том числе и для рассмотренных в данной работе многопроволочных жил. И потому для однозначного определения индуктивности этих проводников необходимы дополнительные соображения.
Цель настоящей работы – такое уточнение понятия индуктивности, которое можно было бы использовать для получения однозначных расчётных величин индуктивных параметров. Имея в виду их связь:
— с геометрией проводов и свойствами их материалов с одной стороны;
— со скоростью распространения электромагнитного поля, волновым сопротивлением и другими наблюдаемыми величинами – с другой стороны;
— а также искробезопасностью и другими эксплуатационными свойствами кабельной продукции.
Решение поставленной задачи обусловило следующий план статьи.
Сначала произведено уточнение подлежащего расчётам индуктивного параметра линий. Потом в среде ELCUT произведено вычисление индуктивности в коаксиальных линиях — простейшем объекте с однозначно определённой величиной индуктивного параметра (как будет показано ниже – это индуктивный инвариант). Главным образом для того, чтобы сравнить результат с точно известным 3) .
Затем произведен расчёт индуктивных параметров многопроволочной жилы, как примера проводника со сложной формой поперечного сечения. А также для проверки с помощью ELCUT наличия у проводников данного типа индуктивного инварианта.
В приложениях приведены некоторые необходимые для применения ELCUT математические рассуждения и доказательство теоремы об «индуктивном инварианте».
Для наглядности и упрощения рассуждений, в данной работе мы рассматриваем объекты, конструкция которых не усложнена скруткой сердечников кабелей и жил в них. Оставив эти вопросы для отдельного обсуждения.
Традиционные определения индуктивности
Существуют разные по физическому смыслу определения индуктивности L (контура, катушки и тд). Кроме определения L в (1), другие связывают этот параметр с:
— эдс Э электромагнитной индукции Э = – L dJ/dt;
— энергией W этого магнитного поля W = L J2/2;
— мнимой частью потока П вектора [E H*] L = Im (П/ω);
Здесь [E H*] – вектор Умова-Пойтинга, П = – ∫ [E H*] dS, dS – элемент поверхности 4) , Н* – комплексно-сопряжённая амплитуда магнитного поля.
Все эти L однозначно определены и математически идентичны, если:
— провода бесконечно тонкие;
— среда, где «живет» магнитное поле, не поглощающая;
— контуры с током точечные.
Из последнего, помимо прочего, следует, что индуктивность – сугубо сосредоточенный параметр.
В линиях связи, силовых кабелях и вообще в системах с распределёнными параметрами не выполняется ни одно из перечисленных условий. Поэтому вводят понятие погонных параметров (их ещё называют первичными): ёмкости С (например, нФ/км) и индуктивности L (мГн/км). Однако в учебной и другой литературе в их определении есть разнобой. И потому уточним, о чём будем говорить.
Индуктивные параметры длинных линий
Рис.1 Схема построения телеграфных уравнений для коаксиального кабеля.
Рассмотрим отрезок z, z +dz двухпроводной линии (рис.1) . Пусть это – коаксиальный кабель c радиусом экрана b и радиусом жилы a (это упростит рассуждения, без умаления их общности). В жиле течёт ток J, распределённый в ней с плотностью σж(r,φ). В экране – противоположный ток с плотностью σэ(r,φ). Если проводимость σ проводников конечна, то на их поверхности есть продольное электрическое поле
Еж = δж/σж и Еэ = δэ/σэ
Здесь δж = δж (а,φ) и δэ = δэ(b,φ) – плотность тока на поверхности жилы и экрана, а σж(а,φ) и σэ(b,φ) – электропроводность. Последняя может меняться по глубине (например, поверхность медных жил может быть лужёной или серебрёной).
В приближении телеграфных уравнений в линии идёт только потенциальная Т-волна. По этой причине для эдс Э индукции по указанному на рисунке контуру (пунктир) можно записать:
– (d/dt) ∫В(r) drdz = Э = – U(z) + Еэdz + U(z + dz) + Ежdz
где: Ф = ∫В(r) drdz – поток магнитной индукции сквозь контур. Отсюда получаем первое телеграфное уравнение (в алгебраической форме):
где: L*= L + R*/ jω – обобщённая погонная индуктивность (далее термин погонный опускаем). В коаксиальной геометрии В(r) = J µ0/2πr, и интеграл легко вычислить:
R* = [ δ э/ σ э + δ ж/ σ ж] / J = Rэ* + Rж*.
Параметр R* обычно называют сопротивлением, так как предел ω -> 0, R* -> R/Д, где: R – суммарное омическое сопротивление постоянному току проводников линии. Д – её длина. А L называют (межпроводной) индуктивностью, по аналогии со сосредоточенной. Хотя по смыслу это – принципиально разные понятия.
Дело в том, что сосредоточенная индуктивность L – это вполне наблюдаемая величина, так как, к примеру, в (1) величины Э и dJ/dt могут быть измерены без разрушения L. Чего нельзя сказать о величинах dU/dz и/или J (z) в (2): их не измерить без разрушения параметров линии. И потому погонная индуктивность L – не наблюдаемый параметр. Равно как и другие первичные параметры длинных линий: межпроводная ёмкость С, сопротивление R и проводимость G = Go + ωC tgδ, где Go – проводимость изолятора на постоянном токе, tgδ – тангенс диэлектрических потерь.
Связь индуктивности с волновыми свойствами и искробезопасностью линий связи
Первичные параметры линий тесно связаны с наблюдаемыми вторичными параметрами: волновым импедансом Z и волновым числом k. А через них – с токами, напряжениями и частотами. Воспользуемся этой связью в телеграфной теории:
Z = [jωL*/(jωC + G)] 1/2 ;
k = [jωL* (jωC + G)] 1/2
Если пренебречь потерями, то
k = jω [(L+Lэ+Lж) C] 1/2 = j ω/V = j 2π/λ
где: L, Lэ, Lж определены ниже, V = 1/ [(L + Lэ+ Lж) C] 1/2 – скорость волны, λ – её длина.
Величина Z = ± U/J определяет связь между амплитудами волн токов и напряжений в линии связи (знак плюс – для волны вдоль z, минус – встречной). И является важнейшей в физике и технике передачи информации.
Она же тесно связана и с искроопасностью кабеля. Пусть, к примеру, на участке Д изоляции провода накопился статический заряд Q, который поднял потенциал этого участка до пробивного уровня U = Q/CД (рис. 2). Тогда в обе стороны от места пробоя полетят волны обнуления потенциала, сопровождаемые скачками разрядного тока J
U/Z . Общая длительность такого пробоя невелика
10 -8 с. К тому же мощность разряда
U2/Z ограничивается сопротивлением Z. И с этой точки зрения его надо увеличивать. То есть увеличивать L + Lэ + Lж и снижать С. Помимо прочего, это хорошо и по той причине, что при этом снижается и освобождаемая в пробое электрическая энергия
Но не всё так просто. Пусть, к примеру, произошёл обрыв в проводе кабеля с Z = 100 Ом и постоянным током J = 10 А (рис. 2 внизу) . Тогда от этого места полетят волны обнуления тока, сопровождаемые скачком напряжения U
1000 В с разными знаками на гранях обрыва. Это явление аналогично экстраэдс индукции
2000 В при обрыве цепей с током, если в в них есть катушки индуктивности. В линиях экстраэдс действует в течение
10 -5 . 10 -6 с – времени, пока волны проходят по линии взад-вперёд и её магнитная энергия рассеивается на концевых нагрузках. Но это в лучшем случае.
Рис.2 «Пробивные» волны в бесконечной длинной линии (жирные горизонтали). Вверху – при пробое изоляции на участке Д накопления статических зарядов. Показаны две расходящиеся волны обнуления статического потенциала U , сопровождаемые волнами разрядного тока J = U/Z . Внизу – аналогичные волны, возникающие при обрыве хотя бы одного проводника с током: волны обнуления тока, сопровождаемые скачком напряжения (до момента возможного пробоя: тогда от точки обрыва в обе стороны полетят волны обнуления потенциала и скачки тока).
В худшем в месте обрыва происходит пробой, и здесь может освободиться почти вся магнитная энергия. И потому для взрывоопасных смесей, сквозь которые проходят некоторые виды кабелей, «индуктивный запал» может оказаться опаснее ёмкостного. В этом случае полезнее как раз уменьшать волновое сопротивление.
В целом может оказаться так, что для коротких линий необходимо подбирать кабели с повышенным Z, а для длинных – наоборот. Или вообще собирать линии связи из кусков с разными Z. Для обеспечения минимальной искроопасности.
Таким образом, как с точки зрения передачи сигналов, так и с точки зрения безопасности, целесообразно рассматривать параметры линии, связанные именно с волновыми свойствами кабелей, как показано в предыдущем разделе.
Вычисляемые компоненты индуктивности
Как видно из (2), обобщённая индуктивность содержит ряд слагаемых:
L* = L + Zэ + Zж = L + Lэ + Rэ/ jω + Lж + Rж/ jω (4)
Которые можно интерпретировать как вклад от межпроводниковой индуктивности L и реактивных составляющих импедансов обоих проводников:
Zэ = Rэ + jω Lэ; Zж = Rж + jω Lж
где, по определению:
Rэ = Re(Zэ); Lэ = Im(Zэ)/ω
Rж = Re(Zж); Lж = Im(Zж)/ω
Lэ = Im(δэ) / (J σэ ω); Rэ = Re(δэ) / (J σэ)
Lж = Im(δж) / (J σж ω); Rж = Re(δж) / (J σж) (5)
Рис.3 К определению величин, необходимых для расчёта индуктивных параметров двухпроводных линий. И доказательства теоремы об индуктивном инварианте.
Здесь и далее мы рассматриваем проводники произвольной формы и симметрии (то есть не обязательно коаксиальной). По этой причине на рис. 3 заменим индексы ж и э числами 1 и 2. Этот рисунок поясняет процедуру вычисления индуктивных параметров, зависящих от выбора контура (поверхности) интегрирования S. Плотности тока проводников δ вычисляем вдоль линиий A1 и A2 касания поверхности S, «натянутой» между проводниками, сквозь которую вычисляем поток Ф = ∫ ВdS в выражении (3). Отметим, что в двумерном случае этот интеграл равен разности вектор-потенциалов линий A2 и A1. Поэтому
Это резко облегчает процедуру расчётов в ELCUT, так как он решает задачу именно для вектор-потенциала А(r,φ).
Так как в проводниках и на их поверхности фазы и амплитуды А(r,φ), δж(r,φ) и δэ(r,φ), вообще говоря, зависят от координат, то индуктивные параметры проводников L, Lэ, Rэ, Lж, Rж не определены однозначно. И, как указано выше, чтобы получить для них определённые величины, нужны дополнительные соображения. Скажем, искробезопасности и/или величины волнового сопротивления линии. Тогда в качестве индуктивности целесообразно использовать максимум суммы L + Lэ + Lж. Тем паче, она – инвариант, то есть определена однозначно (см. Приложение). Проверим всё это с помощью ELCUT, для чего решим ряд простых задач.
Индуктивность однопроволочной жилы и прямой пары
Первая из них – индуктивность однопроволочной медной жилы радиуса а = 0.5 мм в коаксиальном сверхпроводящем экране (Lэ = 0; Rэ = 0) с радиусом b = 1.6 мм . Её межпроводниковая индуктивность L точно известна (для µ = 1):
L = µ µ0 / 2π ln(b/a) = 0.232630 нФ/км
Известны также и параметры провода:
Lж = µ0 / 2π aq [ber ber’ + bei bei’] / D;
Rж = aq / 2 [ber bei’ – ber’ bei] / D (6)
где: q = (ω σ µ0) 1/2 , D = ber’ 2 + bei’ 2 , ber(qa), bei(qa) – функции Томсона (Кельвина), штрихи – их производные.
Задача эта облегчается тем, что в осесимметричном случае А(r,φ) от угла не зависит и потому все указанные в (5) параметры определены однозначно.
Рис.4 Геометрическая модель расчета магнитного поля коаксиальной структуры (верх) и карта магнитного поля (черные кривые – силовые линии) и цветная — плотности тока в жиле линии (тёмно синий цвет – ток = 0) для разных частот.
Проверим это с помощью ELCUT, для чего построим геометрическую модель для коаксиального кабеля (рис.4). Модель представляет собой узкий сектор (100), на лучах которого определены граничные условия Нt = 0, а на внешней дуге – нуль вектор-потенциала А = 0 (приближение — сверхпроводящий экран). Медный жила оборудована вспомогательным ребром (радиус 0.45 мм) для увеличения густоты сетки конечных элементов (всего 251 узлов) в области скин-эффекта. Внизу на рис.4 представлена карта магнитного поля (черные линии) и плотности тока (цвет) при разных частотах. Видно, как по мере увеличения частоты магнитное поле выталкивается из проводника, а электрический ток прижимается к его поверхности (синий цвет – минимальный ток, теплые тона – максимальный). Это и есть скин-эффект.
В таблице приведены значения токов в центре провода δж(0) и δж(а) – на поверхности медного блока (красная точка). Вместе с параметрами L на разных частотах: L = А(а) / J, а также Lж и Rж. Справа от них – ошибки относительно расчётов по формулам (6).
Из таблицы видно, как с увеличением частоты падает амплитуда тока в центре провода, меняя при этом знак, и растёт ток на поверхности.
ELCUT с высокой степенью точности подтверждает, что в коаксиальных структурах параметр L не зависит от частоты (то есть определён однозначно). На частотах выше 1 МГц быстро растут ошибки вычислений в ELCUT параметров Rж и, особенно, Lж. Это, видимо, связано с развитием скин-эффекта, который заставляет увеличивать густоту сетки в приповерхностных слоях проводника. Но доступная версия ELCUT (255 узлов) не позволяет установить этот факт с надлежащей достоверностью. Тем не менее, даже в этой версии погрешность Rж относительно величины ωL не превышает 0.05% (в среднем 0.04%), а Lж 0.2% (0.12%). Во всём практически интересном диапазоне частот от 100Гц до 1000 МГЦ.
Для справок в таблице приведены значения глубины проникания (диффузии) магнитного поля в медь. Например, на частоте 1 МГц поле проникает в проводник на глубину
0,2 мм. В этом же слое в основном текут токи. Что и приводит к росту на полпорядка сопротивления провода Rж и такому же падению его индуктивности Lж. На рис.5 синие точки – расчёт Rж и Lж в ELCUT, а кривые – точное решение (6). Совпадение впечатляет. Особенно, если учесть, что ELCUT не знает о существовании функций Бесселя, Томсона, Макдональда . Светлые точки на рисунке – кривая для семипроволочной жилы (см. ниже).
Рис.5 Зависимость от частоты сопротивления жилы Rж (верхний график) и его индуктивности Lж (нижний). Синие точки — расчёт ELCUT, кривые – точное решение (см. текст). Светлые точки – для семипроволочной жилы.
Так как конформные отображения не меняют вид уравнения Лапласа ΔА = 0, индуктивность L коаксиального кабеля совпадает с аналогичным параметром всех его конформных отображений. В том числе симметричной прямой пары с соотношением
(для рассматриваемого кабеля b’/a’ = 1.173936).
С другими индуктивными параметрами ситуация посложнее, так как для их вычислений необходимо решать уравнения Пуассона ΔА = – µµ0δ, а конформные отображения, вообще говоря, меняют его вид, что исключает возможность прямого применения ELCUT. Задача, однако, облегчается тем обстоятельством, что дробно-линейное отображение практически не меняет вид и этого уравнения (см. Приложение). По этой причине результаты, полученные для коаксиальной структуры, полностью отображают свойства конформной ей пары.
Кроме того, в рассмотренной выше задаче экран был сверхпроводящим (Lэ = 0; Rэ = 0). А в симметричной паре он медный, и его роль можно учесть просто удвоением величин Rж и Lж, так как Rэ = Rж и Lэ = Lж. Полученные в данном разделе результаты могут быть применены и для несимметричных пар, то есть с разным диаметром и/или металлом жил. Для чего требуется лишь небольшое усложнение методики расчёта.
Индуктивность многопроволочной жилы
Рассмотрим коаксиальный кабель с жилой из семи проволок и сверхпроводящим экраном. Пусть площадь меди в жиле такое же, как рассмотренном выше примере (Ø = 1 мм, 0.785398 мм 2 ) . Тогда диаметр проволоки 0.377964 мм, «большой» диаметр жилы 1.133893 мм, «малый» 1.032618 мм. А радиус экрана b = 1.814229 мм.
У конструкции есть ось симметрии шестого порядка и 12 плоскостей симметрии, поэтому расчёты производим в секторе 360/12 = 30 0 . На рис.6 представлен фрагмент геометрической модели с указанием характерных рёбер и точек (красные), для которых вычисляли вектор-потенциал, плотность тока и поток магнитной индукции. А также карты магнитного поля и токов для разных частот (рис.6). Видно, как семипроволочная жила выталкивает из своего объёма магнитное поле, а её ток прижимается к вершине внешней проволоки.
Рис.6 Геометрическая модель и карта магнитных полей (черные кривые) и плотности токов (синий цвет – ток = 0) для семипроволочной жилы, размещённой коаксиально относительно сверхпроводящего экрана для разных частот. Видно, как по мере увеличения частоты ток жилы оттесняется к её поверхности, а магнитное поле выталкивается из жилы. Красные линии на геометрической модели – контуры интегрирования для вычисления максимальной (контур К) и минимальной (В) величины межпроводниковой индуктивности L.
Синим пунктиром на карте 1 МГц обозначен радиус однопроволочной жилы (Ø = 1.0656 мм), которая имеет тот же индуктивный инвариант L + Lж, что и семипроволочная (см ниже). Частотный ход сопротивления многопроволочной жилы подобен однопроволочной того же сечения, причём на низких частотах они просто совпадают (рис. 5) . На высоких частотах сопротивление многопроволочной жилы заметно больше, так как работает только часть её поверхности.
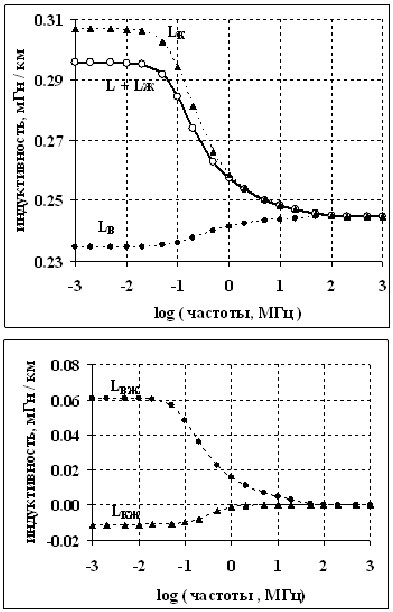
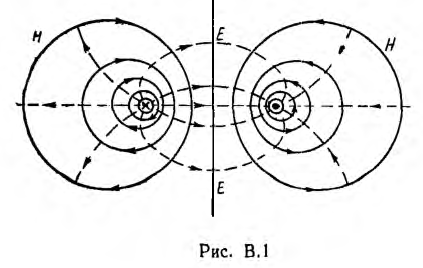
Но намного интереснее частотный ход индуктивного параметра L, отображённый на рис. 7. Как указано выше, здесь именно тот случай, когда межпроводная индуктивность зависит от выбора контура, а параметр Lж – от точки на поверхности жилы. Для наглядности через расчётные точки ELCUT проведены кривые.
Рис.7 Частотная зависимость индуктивных параметров семипроволочной жилы, вычисленных для разных контуров и индуктивного инварианта L + Lж (см. текст).
Действительно, как видно из рисунка, индуктивность LK, вычисленная по контуру К (верхняя красная линия геометрической модели) заметно больше, чем LB, вычисленная по контуру В (нижняя линия). На частотах больше
1 МГц, то есть по мере «отключения» проводника, это различие сходит на нет. И такое поведение понятно. Как видно из картины полей, на низких частотах магнитное поле проходит сквозь металл и поток магнитной индукции через контур К, больше. На высоких частотах поле выталкивается из проволок, и различие стирается.
Как видно из рис.7, индуктивный параметр LКЖ отрицательный. То есть металл в заглублении поверхности работает как бы «против» общей индуктивности. Аналогично встречно включённой обмотке трансформатора. Но самая интересная особенность этих расчётов ELCUT в том, что на всех частотах с погрешностью 2) аналогичный радиус был найден для ёмкости семипроволочной жилы. Причём его величина численно совпадает с индуктивным. Видимо, это связано с теоремой об обратном отношении межпроводных ёмкостей и индуктивностей.
Выводы
1. Погрешность расчётов индуктивных параметров
0.1..0.3% в программной среде ELCUT не превышает погрешность ёмкостных.
2. Межпроводная индуктивность L и индуктивные параметры Lж не осесимметричных жил не имеют однозначного определения. Однако, однозначно определён инвариантный индуктивный параметр L + Lж .
3. Многопроволочную жилу (и вообще произвольной формы) можно заменить круглым проводом с некоторым эффективным радиусом, который для наиболее характерных форм кабельных жил и их окружения можно вычислить раз и навсегда.
Конформное отображение уравнений Лапласа и Пуассона
Функция w(z) = u + j v где z = x + jy, а u (х,у) и v(x,y) удовлетворяют условиям
реализует конформное преобразование фигур (образов) из плоскости х, у в их отображения в плоскости u, v. А функции х(u,v) и у(u,v) – обратное отображение.
В операторе Лапласа это просто замена переменных:
Таким образом, конформное преобразование не меняет вид уравнения Лапласа:
Но, вообще говоря, меняет вид уравнения Пуассона. Во всяком случае, его правой части. Например, для потенциала U электрического поля
где = ρ (х, у) и ρ (u,v) – плотность заряда.
Она имеет смысл производной ρ = dQ / dS, где Q (x,y) – функция распределения заряда по поверхности, а dS = dxdy – элемент площади. При замене переменных элемент площади трансформируется
dS’ = dudv = (∂(u,v) / ∂(x,y))1/2 dxdy = √|D| dxdy
Подставим это в (*):
D (Uuu + Uvv) = – dQ(х(u,v), у(u,v))/(εε0 dudv/√|D|)
И получаем уравнение Пуассона в переменных u, v ΔU(u,v) = – ρ (х, у) / εε0, где ρ(u,v) = dQ(х(u,v), у(u,v)) / (dudv √|D|) = ρ(х(u,v), у(u,v)) / √|D|
Таким образом, чтобы получить «новую» плотность заряда, надо в «старой» заменить х,у на u,v, и разделить на √|D|. Отметим, что если в правой части уравнения Пуассона не плотность зарядов, а,скажем, точечный заряд, то его надо разделить на D.
Более того, дробно-линейное конформное отображение сохраняет вид не только уравнения Лалпаса, но и Пуассона.
Доказательство
Пусть в плоскости x,y действует дробно-линейное отображение w = M 2 /z .
Тогда u = M 2 x / r 2 и v = – M 2 y / r 2 и обратно: x = M 2 u / R 2 и y = – M 2 v / R 2 ,
где: r 2 = x 2 + y 2 ; R 2 = u 2 + v 2 = M 4 /r 2 .
В этом случае D = (∂(R,φ) / ∂(r,φ)) = – M 2 /r 2 . А уравнение Пуассона (в полярных координатах):
Аналогично для вектор-потенциала магнитного поля
Arr + Ar/r + Aφφ /r 2 = – δ(r, φ)/εε0; ARR + AR/R + Aφφ/R 2 2 = – δ(M 2 /R, φ) M 2 /(R 2 εε0), где δ – плотность тока.
Видно, что все уравнения отличаются только обозначением переменных. Что и требовалось доказать.
Индуктивный инвариант
Исходим из телеграфного уравнения
– (∂/∂t) ∫ В(r) dr = Uz + Еэ + Еж (**)
где: Еэ = δэ / σэ, Еж = δж/σж. Запишем в алгебраической форме
– jωLJ = Uz – Re(δэ) / σэ – j Im(δэ) / σэ – Re(δж) / σж – j Im(δж) / σж
– jωJ (L – Im(δж) / Jωσж – Im(δэ) / Jωσэ) = Uz – Re(δэ) / σэ – Re(δж) / σж)
по определению Im(δж) / Jδσж = – Lж, Im(δэ ) / Jωσ = – Lэ.
– jωJ (L + Lж + Lэ) = Uz – Re(δэ) / σэ – Re(δж) / σж
Правая часть зависит от (градиента) потенциала сечения плоскостью z поверхности проводов. В приближении телеграфных уравнений это сечение – линия равного потенциала и его градиентов. Следовательно, правая часть не зависит от положения точек на указанной линии. Следовательно, такой же инвариант и величина L + Lж + Lэ. Если один из проводников, например, экран – сверхпроводящий, то Lэ = 0 и инвариант вырождается в L + Lж. Что и требовалось доказать.
1) Вишняков Е.М., Хвостов Д.В. Расчёт межпроводниковой индуктивности и ёмкости симметричных прямых пар методами конформных отображений и конечных элементов. Кабель №3, 2007.
2) Вишняков Е.М., Хвостов Д.В. Влияние скрутки на межпроводниковую ёмкость витых пар и триад. Кабель №4, 2007.
3) П.Л.Калантаров, Л.А.Цейтлин. Расчёт индуктивностей. – Л:Энергоатомиздат, 1986, стр. 94.
4) Л.А.Бессонов. Теоретические основы электротехники.– М: ВШ, 1967
Нашли ошибку? Выделите и нажмите Ctrl + Enter
Видео:Электромагнитная индукция. Простыми словамиСкачать

Электрическая ёмкость и ее расчет
Содержание:
Электротехника и ее теоретические основы:
Одной из основных задач техники является преобразование при родных энергетических запасов в используемые виды энергии — в механическую, тепловую, световую и т. п., что требует транспортировки энергетического сырья к месту его использования.
Электрическая энергия легко передается на большие: расстояния и с высоким коэффициентом полезного действия преобразуется в другие виды энергии. Общепринятым является преобразование природных энергетических запасов в электрическую энергию с помощью так называемых генераторов и ее передача посредством проводов к месту потребления, где в преобразователях и приемниках она преобразуется в нужный вид энергии. Беспроводная передача энергии осуществляется с помощью радиосвязи.
Преимущества генерирования, передачи, распределения и преобразования электрической энергии обеспечили широкое применение электротехники.
Новые производственные отношения в нашей стране, отсутствие частной собственности на запасы энергетического сырья, средства и орудия производства, государственное планирование являются мощным фактором развития электротехники и всеобъемлющего охвата ею всех отраслей нашего народного хозяйства, быта и культуры.
Составленный под руководством В. И. Ленина план ГОЭЛРО построения 30 электростанций общей мощностью 1,75 млн. кет был выполнен в решающих позициях за 10 лет.
В послевоенные годы электрификация СССР развивается невиданными темпами: в 1960 г. мощность электростанций составила 66,7 млн. кет, а за пятилетку 1966— 1970 гг. введены 54 млн. кет, в том числе самая мощная в мире Красноярская гидроэлектростанция (6 млн. кет) и Белоярская атомная электростанция (600 тыс. кет). В Директивах XXIV съезда КПСС по пятилетнему плану развития народного хозяйства СССР на 1971— 1975 гг. предусмотрено ввести в действие электростанции мощностью 65—67 млн. кет, в том числе 6—8 млн. кет на атомных электростанциях. Соответственно увеличилась и увеличится мощность потребителей — устройств, преобразующих электрическую энергию в другие виды.
Электрическая энергия — это энергия электромагнитного поля, являющегося видом материи. Поле имеет две составляющие — электрическое и магнитное поля, что можно показать на примере линии передачи постоянного тока (рис. В. 1).
При передаче энергии провода линии, изолированные друг от друга, находятся под напряжением U. Следовательно, между проводами возникает электрическое поле, изображенное пунктиром на рис. В.1 в виде силовых линий, В проводах протекает ток 7, следовательно, в проводах и вне их создается магнитное поле, показанное сплошными линиями. На рис. В.1 видно характерное различие между электрическим и магнитным полями: силовые линии электрического поля незамкнуты, они начинаются и оканчиваются на заряженных проводах; магнитные силовые линии всегда замкнуты; они не имеют ни начала, ни конца.
Как известно из курса физики, электрическое поле в каждой точке
характеризуется вектором напряженности Е, равным силе, воздействующей на единичный положительный заряд, помещенный в эту точку, и вектором электрического смещения
Электрическое поле в проводящей среде создает ток, характеризуемый в
каждой точке поля вектором плотности тока 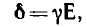
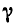
проводимость среды. Ток сопровождается появлением магнитного поля и переходом части энергии электромагнитного поля в тепло, причем мощность этого процесса в единице объема
Магнитное поле в каждой точке характеризуется вектором магнитной индукции В, величина которого равна силе, действующей на движущийся единичный положительный заряд, скорость которого равна единице, а направление В — перпендикулярно этой силе и скорости, а также вектором напряженности
где 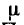
Передача, генерирование, преобразование и потребление электрической энергии, равной 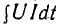
В науке об электричестве связь электрических и магнитных явлений была установлена в двадцатых годах прошлого века, когда Ампер и Эрстед доказали, что электрический ток сопровождается возникновением магнитного поля; окончательно связь электрического и магнитного полей была подтверждена Фарадеем, открывшим явление электромагнитной индукции (1831 г.).
Электротехника, зародившаяся в тридцатых годах прошлого века, вначале развивалась как техника постоянного тока. Только после создания М. О. Доливо-Добровольским системы трехфазного тока и трехфазного двигателя (1891 г.) переменный ток стал вытеснять постоянный. Передача электрической энергии стала осуществляться также трехфазным током.
Теория электромагнитного поля в законченной математической форме была создана Максвеллом в 1873 г. Подтвержденная многочисленными опытами ряда ученых, она была окончательно принята в начале нашего века.
Введенное Максвеллом представление об электромагнитных волнах, экспериментально подтвержденное работами Герца, позволило А. С. Попову в 1895 г. осуществить передачу сигнала без проводов, что послужило началом новой области электротехники — радиотехники.
Электротехника и ее теоретические основы непрерывно развиваются. Например, совершенствуются электронные, ионные и полупроводниковые приборы и аппараты, с помощью которых осуществляют прямые и обратные преобразования переменного тока в постоянный, усиление напряжения и мощности и создают электронные вычислительные машины. Увеличивается дальность и возможности проводной связи, радиотехники и телевидения, развивается электроавтоматика, в энергетике осуществляется переход к большим напряжениям (1500 кв) и мощностям генераторов (1 200 ООО кет и выше), разрабатываются и испытываются магнитогидродинамические прямые преобразователи тепловой энергии в электрическую и т. д.
Так как все электротехнические устройства основаны на использовании электромагнитного поля их систем, состоящих из заряженных тел и контуров с токами, для решения многих задач необходимо привлечение теории этого поля со сложными математическими зависимостями. Однако в большинстве устройств используются ограниченные пути электрического тока и магнитного потока — изолированные проводники малого сопротивления и магнитопроводы из материала с высокой магнитной проницаемостью, называемые электрическими и магнитными цепями. Их расчеты могут быть значительно упрощены, так как не требуют знания составляющих поля в каждой точке устройств. Теория этих цепей основана на использовании интегральных величин: напряжения 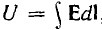
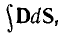
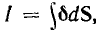
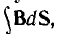
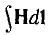
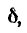
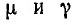
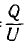
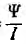
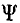
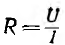
Эти величины можно называть параметрами цепей.
Если эти параметры не зависят от токов и напряжений, уравнения теории цепей, связывающие интегральные величины, будут линейными; такие цепи называют линейными.
В ряде случаев, весьма важных для современной электротехники, эти параметры являются функциями напряжений и токов; тогда уравнения и цепи становятся н нелинейными.
Осуществление грандиозных планов дальнейшей электрификации нашей страны, эксплуатация существующих и создание новых электротехнических устройств требуют от инженера-электрика глубокого понимания физических процессов и умения производить их технический расчет. Фундаментом электротехнического образования является курс теоретических основ электротехники (ТОЭ), базирующийся на сведениях, сообщенных в курсах физики, математики и механики.
Настоящее учебное пособие ТОЭ построено в соответствии с изложенным. Вначале даны параметры цепей, потом основы теории источников и приемников электрической энергии. Затем следует анализ электрических и магнитных цепей при постоянном и переменном токе — линейных и на их основе нелинейных. Курс завершается теорией постоянного и переменного электромагнитного поля.
В книге принята Международная система единиц СИ и рационализованная форма написания уравнений, предложенная Хевисайдом, в которой основные соотношения для электрического и магнитного полей имеют симметричный вид, а множители 4 π и 2 π входят лишь в те соотношения, где они соответствуют характеру симметрии — сферической (4 π) и осевой (2 π).
Видео:53. Теорема о циркуляции вектора индукцииСкачать

Параметры электрических и магнитных цепей
Электрической цепью называется совокупность устройств, состоящая из источников, преобразователей и приемников электрической энергии и соединяющих их проводов, образующих замкнутые пути для электрического тока.
Часть цепи, не содержащая источников электрической энергии, называется пассивной, а часть цепи, содержащая источники, называется активной.
Как было показано во введении на примере линии передачи, электрическая цепь характеризуется тремя параметрами: сопротивлением R, емкостью С и индуктивностью L. Этими параметрами обладают все элементы цепей, например резисторы, в которых основную роль играет их сопротивление, конденсаторы с основным параметром — емкостью, и катушки индуктивности, в которых основной является их индуктивность.
Из изложенного вo введении очевидно, что параметры линии передачи равномерно распределены по всей длине линии. Параметры распределены также в отдельных элементах цепи. Например, в катушке индуктивности сопротивление, индуктивность и емкость распределены по ее длине, так как каждый виток с током имеет сопротивление и создает магнитное поле, а отдельные витки изолированного проводника обладают друг по отношению к другу некоторой емкостью.
Этим свойством обладают все реальные электрические цепи—они являются цепями с распределенными параметрами. Так как в ряде технически важных задач не требуется знания электромагнитных процессов в каждой точке всей цепи и ее элементов, необходимо учесть только их интегральные свойства; такие цепи могут быть представлены в виде цепей с сосредоточенными параметрами, состоящих из сопротивлений, индуктивностей и емкостей. Например, катушка индуктивности может быть представлена в виде схемы с последовательным соединением сопротивления R, индуктивности L и с параллельно приключенной к ним емкостью С.
При включении цепи на постоянное напряжение в течение короткого времени от источника потребляется энергия на создание электромагнитного поля. После этого запасенная в С и L энергия сохраняет свою величину неизменной и не отражается на работе цепи, а источники доставляют энергию только на покрытие тепловых потерь в сопротивлениях. Поэтому при расчете цепей постоянного тока следует учитывать только сопротивление R.
В цепях переменного тока энергия, запасаемая в С и L, и мощность потерь в R непрерывно изменяются. Поэтому при расчете этих цепей необходимо учитывать все три параметра.
Многие электрические цепи нелинейны. Так, например, температура, а следовательно, и сопротивление проводника при прохождении по нему тока изменяются; индуктивность катушки со стальным сердечником зависит от тока, так как с величиной тока будет меняться магнитная проницаемость р, сердечника, а следовательно, и индуктивность L. Однако в большинстве случаев цепи можно рассматривать как линейные, считая параметры R, L и С постоянными.
В устройствах современной электротехники главным образом используется энергия магнитного поля, поэтому их основным параметром является индуктивность L. Для этих устройств вводится понятие магнитной цепи как совокупности тел, большей частью ферромагнитных, в которых создается магнитный поток.
При постоянном токе методы анализа магнитных цепей аналогичны методам расчета электрических цепей, содержащих лишь один параметр — сопротивление R. Его аналогом в магнитных цепях является магнитное сопротивление 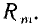
Эта глава посвящена элементарным методам расчета параметров устройств, поля которых имеют простые виды симметрии. Более сложные случаи рассматриваются в теории электромагнитного поля.
Видео:ЧК_МИФ_3_4_5_1_(L3)_УРАВНЕНИЕ ДЛЯ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В КОАКСИАЛЬНОМ КАБЕЛЕСкачать

Электрическая ёмкость и ее расчет
Для электрических цепей наибольший интерес представляет система двух проводящих тел в диэлектрической среде, заряды + Q и —Q которых отличаются только знаком, являющаяся по существу конденсатором. Емкость конденсатора равна отношению его заряда Q, под которым понимается абсолютное значение разноименных зарядов, к напряжению U между обкладками:
Емкость конденсатора, определяемая размерами и формой тел и их взаимным расположением, пропорциональна диэлектрической проницаемости е среды между обкладками. Емкость измеряется Б фарадах (ф), заряд в кулонах (к), напряжение в вольтах (в).
Для расчета емкости конденсатора по заряду и напряжению необходимо предварительно рассчитать его электрическое поле, исходя из общих соотношений для электрического поля.
Связь между зарядом и вектором смещения 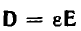
справедливой для линейных и нелинейных сред и являющейся основным соотношением для электрического поля. В правой части этого равенства стоит суммарный заряд, заключенный внутри замкнутой поверхности, в левой — поток вектора смещения. Смещение измеряется в к/м2, напряженность электрического поля — в в/м, диэлектрическая проницаемость в ф/м.
Поле в каждой точке характеризуется потенциалом 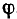
Напряжение 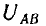
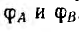
Потенциал также измеряется в вольтах.
Так как сумма напряжений по замкнутому пути равна нулю, то 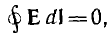
Емкость коаксиального кабеля
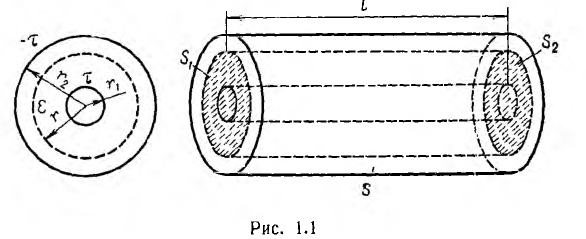
Коаксиальный кабель представляет собой два проводящих соосных
цилиндра с радиусом внутреннего цилиндра r1 внутренним радиусом
внешнего цилиндра г2, длиной цилиндров I (рис. 1.1).
Пусть внутренний цилиндр — жила кабеля — заряжен положительно и изолирован диэлектриком с проницаемостью е от оболочки — обратного провода, являющегося внешним цилиндром и несущим заряд обратного знака, а напряжение между жилой и оболочкой равно U.
При выполнении условия 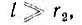
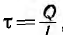
Для цилиндрической поверхности радиуса г, охватывающей заряженную жилу (на рис. 1.1 указана пунктиром), можно применить теорему Гаусса. Из- за радиального направления вектора смещения потоки через основания цилиндра 
Так как при неизменном радиусе смещение D остается постоянным, то
В последние выражения не входит радиус 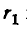
Напряжение на кабеле
откуда емкость кабеля
После подстановки из предпоследнего равенства
в выражение для напряженности поля получим
т .е . напряженность поля обратно пропорциональна радиусу, а ее максимальное значение у поверхности жилы
Исследование на минимум показывает, что наименьшее значение
максимальной напряженности при заданных напряжении и радиусе 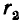
внешней оболочки будет при
т. е. при 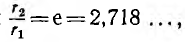
При таком соотношении радиусов кабель, очевидно, обладает наибольшей электрической прочностью.
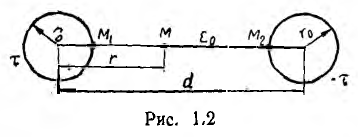
Емкость двухпроводной линии
Широко используемые в электротехнике двухпроводные линии передачи представляют собой систему двух прямых параллельных проводов кругового сечения (рис. 1.2). Провода оказываются заряженными разноименно, когда линия включена на напряжение.
Так как длина проводов I велика по сравнению с расстоянием d между их осями, искажением электрического поля у концов заряженных проводов можно пренебречь. Поэтому распределение поля в пространстве остается неизменным в любой плоскости, перпендикулярной осям проводов.
Пусть двухпроводная линия подвешена настолько высоко, что влиянием земли можно пренебречь. Напряжение на линии равно U, величина заряда на единицу длины — τ, радиус проводов — 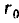
В отличие от коаксиального кабеля, где вследствие равномерного распределения заряда по поверхности жилы ее электрическая ось совпадает с геометрической, плотность зарядов на проводах линии больше на частях их поверхностей, обращенных друг к другу из-за притяжения разноименных зарядов. Поэтому расстояние между электрическими осями проводов становится тем меньше расстояния между их геометрическими осями, чем меньше отношение 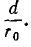
Для воздушных линий 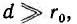
где 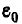
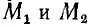
Отсюда емкость двухпроводной воздушной линии
Взаимоёмкость и ее расчёт
Для многих технических задач представляет интерес рассмотрение электрического поля, созданного системой нескольких пар разноименно заряженных тел. Заряды этих тел и напряжения связаны между собой линейными уравнениями.
В системе из двух конденсаторов (1-1′ и 2-2′ на рис. 1.3) все четыре тела связаны электрическим полем, поэтому заряд каждого из конденсаторов зависит от их напряжений 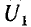
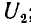
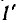
напряжением второго, совпадает по знаку с зарядом, создаваемым собственным напряжением, суммарные заряды обоих конденсаторов будут:
где 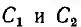
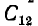
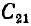
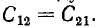
Собственные емкости конденсаторов
определяются всеми четырьмя телами системы и отличаются от емкости каждого из этих конденсаторов, определенной при отсутствии другого.
При определении ёмкости 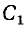
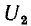
Соответственно, при определении 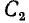
т. е. равна отношению заряда на обкладках накоротко замкнутого одного конденсатора, когда его заряд создается напряжением другого, к этому напряжению.
Взаимоемкость определяется конфигурацией тел, образующих конденсаторы, их взаимным расположением и пропорциональна диэлектрической проницаемости среды.
При несовпадении знаков собственных зарядов, обусловленных емкостью, и взаимных зарядов, обусловленных взаимоемкостью, знак перед вторыми членами в выражениях (1.2) будет отрицательным. Взаимоемкость также измеряется в фарадах (ф).
Для системы многих конденсаторов, соответственно, заряд Qk
конденсатора k определяется всеми напряжениями:
где 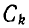
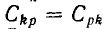
Взаимоемкость между конденсаторами k и р равна отношению заряда конденсатора k, созданного напряжением конденсатора р, к этому напряжению. При этом все конденсаторы, кроме p -того, замкнуты накоротко.
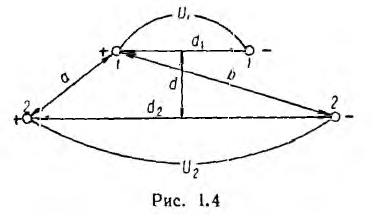
Взаимоемкость двух параллельных двухпроводных линий
Примером системы из четырех тел, рассматриваемой как совокупность двух конденсаторов, могут служить две параллельные линии, расположенные симметрично одна над другой (рис. 1.4).
Пусть радиус проводов 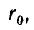
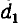
и 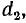

Заряды на проводах первой линии замкнутой накоротко 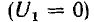
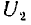
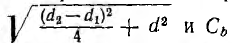
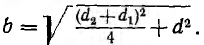
Тогда, соответственно формуле (1.1), получается
а собственная емкость первой линии при учете второй линии равна
Такая задача представляет технический интерес, позволяя определить влияние линии передачи 2 на линию связи 1 (рис. 1.4).
Это влияние состоит в наведении на проводах линии связи заряда взаимоемкости 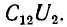
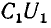
а напряжение 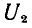
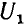
линии связи, то для уменьшения наведенного заряда необходимо увеличивать расстояние d между линиями и уменьшать расстояние 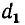
между проводами линии связи.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейные н нелинейные диэлектрики и конденсаторы
- Сопротивление и его расчет
- Линейные и нелинейные резисторы
- Индуктивность и ее расчет
- Преобразование схем электрических цепей
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔥 Видео
S11, S21 методы измерения потерь в кабеле на NanoVNAСкачать

КОАКСИАЛ, коаксиальный кабель, линии, колебательные контуры, трансформаторы, фильтрыСкачать
Измерение параметров коаксиального кабеля с помощью NanoVNAСкачать
ЭМ Л26. 2023. Индуктивность коаксиального кабеля. Переходные процессы с L и C. Колебательный контурСкачать

Антенный и коаксиальный кабель на 50 и 75 Ом. Больше, чем вы знаете!Скачать

Коаксиальные кабели. Разбираемся вместе.Скачать

Измерение волнового сопротивления коаксиальных кабелейСкачать

Коаксиальный кабель.Что надо знать,почему плохо работает и тест 4 разных кабелейСкачать

Измеряем потери в коаксиальном кабелеСкачать

Затухание в коаксиальном кабеле, 3 замера.Скачать

Демонстрация (2/2) влияния некачественного соединения коаксиального кабеля на его параметрыСкачать

Демонстрируем способ обжима коаксиального кабеля 8D-FB CCA LSZHСкачать

Как проверить качество коаксиального кабеляСкачать

Сколько потери в коаксиальном кабеле RG-6UСкачать

Почему наконечник кабеля прессовать нужно сверху вниз? #энерголикбез #за40секСкачать

NanoVNA Как правильно измерить волновое сопротивление коаксиального кабеляСкачать