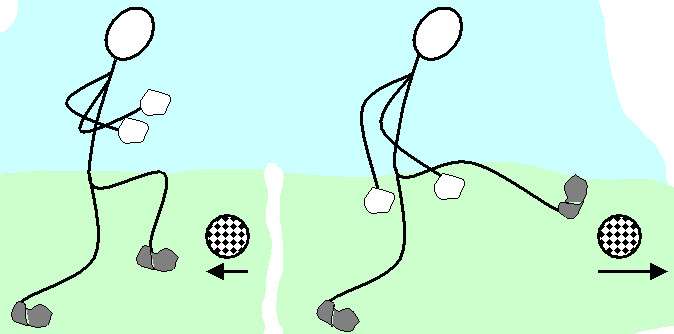
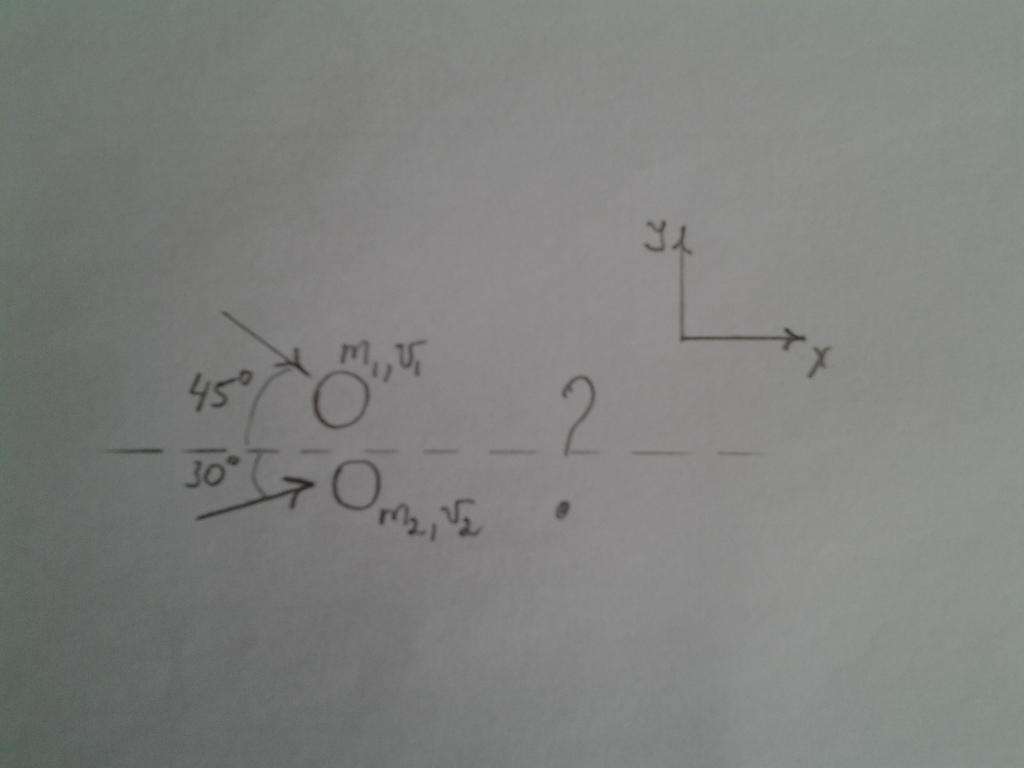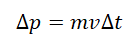Любые задачи на движущиеся тела в классической механике требуют знания концепции импульса. В данной статье рассматривается эта концепция, дается ответ на вопрос, куда направлен вектор импульса тела, а также приводится пример решения задачи.
- Количество движения
- Импульс силы — причина изменения количества движения
- Векторная величина p¯
- Куда направлен вектор импульса тела?
- Вектор изменения количества движения
- Где важно учитывать векторный характер количества движения?
- Задача с двумя шарами
- Импульс тела, закон сохранения импульса
- теория по физике 🧲 законы сохранения
- Относительный импульс
- Изменение импульса тела
- Частные случаи определения изменения импульса тела
- Абсолютно неупругий удар
- Абсолютно упругий удар
- Пуля пробила стенку
- Радиус-вектор тела повернул на 180 градусов
- Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
- Второй закон Ньютона в импульсном виде
- Реактивное движение
- Суммарный импульс системы тел
- Закон сохранения импульса
- Закон сохранения импульса в проекции на горизонтальную ось
- Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
- Сохранение проекции импульса
- Импульс, закон сохранения импульса
- 💡 Видео
Видео:Физика - движение по окружностиСкачать

Количество движения
Чтобы выяснить, куда направлен вектор импульса тела, следует, в первую очередь, понять его физический смысл. Впервые термин был объяснен Исааком Ньютоном, однако важно отметить, что итальянский ученый Галилео Галилей в своих работах уже использовал похожее понятие. Для характеристики движущегося объекта он ввел величину, которая называлась стремление, натиск или собственно импульс (impeto на итальянском). Заслуга же Исаака Ньютона заключается в том, что он смог связать эту характеристику с действующими на тело силами.
Итак, изначально и более правильно то, что большинство понимают под импульсом тела, называть количеством движения. Действительно, математическая формула для рассматриваемой величины пишется в виде:

Здесь m — масса тела, v¯ — его скорость. Как видно из формулы, ни о каком импульсе речь не идет, имеется лишь скорость тела и его масса, то есть количество движения.
Важно отметить, что эта формула не следует из математических доказательств или выражений. Ее возникновение в физике имеет исключительно интуитивный, бытовой характер. Так, любой человек хорошо представляет, что если муха и грузовик будут двигаться с одинаковой скоростью, то грузовик остановить гораздо тяжелее, поскольку он обладает намного большим количеством движения, чем насекомое.
Откуда возникло понятие вектор импульса тела, рассмотрено далее.
Видео:Импульс тела и импульс силы. Закон сохранения импульса. 10 класс.Скачать

Импульс силы — причина изменения количества движения
Интуитивно введенную характеристику Ньютон смог связать со вторым законом, носящим его фамилию.
Импульс силы — это известная физическая величина, которая равна произведению приложенной внешней силы к некоторому телу на время ее действия. Воспользовавшись известным законом Ньютона и полагая, что сила от времени не зависит, можно прийти к выражению:
F¯ * Δt = m * a¯ * Δt.
Здесь Δt — время действия силы F, a — это линейное ускорение, сообщаемое силой F телу массой m. Как известно, умножение ускорения тела на промежуток времени, который оно действует, дает приращение скорости. Этот факт позволяет переписать формулу выше в несколько ином виде:
F¯ * Δt = m * Δv¯, где Δv¯= a¯ * Δt.
Правая часть равенства представляет собой изменение количества движения (см. выражение в предыдущем пункте). Тогда получится:
F¯ * Δt = Δp¯, где Δp¯ = m * Δv¯.
Таким образом, пользуясь законом Ньютона и понятием об импульсе силы, можно прийти к важному выводу: воздействие внешней силы на объект в течение некоторого времени приводит к изменению его количества движения.
Теперь становится понятным, почему количество движения принято называть импульсом, ведь его изменение совпадает с импульсом силы (слово «сила», как правило, опускают).
Видео:Физика - импульс и закон сохранения импульсаСкачать

Векторная величина p¯
Над некоторыми величинами (F¯, v¯, a¯, p¯) стоит черта. Это означает, что речь идет о векторной характеристике. То есть количество движения так же, как и скорость, сила и ускорение, помимо абсолютной величины (модуля), описывается еще направлением.
Так как каждый вектор можно разложить на отдельные компоненты, то, пользуясь декартовой прямоугольной системой координат, можно записать следующие равенства:
2) px = m * vx; py = m * vy; pz = m * vz;
3) |p¯| = √(px2 + py2 + pz2).
Здесь 1-е выражение — это векторная форма представления количества движения, 2-й набор формул позволяет рассчитать каждую из компонентов импульса p¯, зная соответствующие компоненты скорости (индексы x, y, z говорят о проекции вектора на соответствующую ось координат). Наконец, 3-я формула позволяет вычислить длину вектора импульса (абсолютное значение величины) через его компоненты.
Видео:Урок 104. Импульс. Закон сохранения импульсаСкачать

Куда направлен вектор импульса тела?
Рассмотрев понятие количества движения p¯ и его основные свойства, можно легко ответить на поставленный вопрос. Вектор импульса тела направлен так же, как и вектор линейной скорости. Действительно, из математики известно, что умножение вектора a¯ на число k приводит к образованию нового вектора b¯, обладающего следующими свойствами:
- его длина равна произведению числа на модуль исходного вектора, то есть |b¯| = k * |a¯|;
- он направлен так же, как исходный вектор, если k > 0, в противном случае он будет направлен противоположно a¯.
В данном случае роль вектора a¯ играет скорость v¯, импульс p¯ — это новый вектор b¯, а число k — это масса тела m. Поскольку последняя всегда является положительной (m>0), то, отвечая на вопрос: чему сонаправлен вектор импульса тела p¯, следует сказать, что он сонаправлен скорости v¯.
Видео:Момент импульса. 10 класс.Скачать

Вектор изменения количества движения
Интересно рассмотреть еще один похожий вопрос: куда направлен вектор изменения импульса тела, то есть Δp¯. Для ответа на него стоит использовать полученную выше формулу:
F¯ * Δt = m * Δv¯ = Δp¯.
Исходя из рассуждений в предыдущем пункте, можно сказать, что направление изменения количества движения Δp¯ совпадает с направлением вектора силы F¯ (Δt > 0) или с направлением вектора изменения скорости Δv¯ (m > 0).
Здесь важно не путать, что речь идет именно об изменении величин. В общем случае векторы p¯ и Δp¯ не совпадают, поскольку они никак не связаны друг с другом. Например, если сила F¯ будет действовать против скорости v¯ перемещения объекта, тогда p¯ и Δp¯ будут направлены в противоположные стороны.
Видео:Импульс тела. Закон сохранения импульса | Физика 9 класс #20 | ИнфоурокСкачать

Где важно учитывать векторный характер количества движения?
Рассмотренные выше вопросы: куда направлен вектор импульса тела и вектор его изменения, обусловлены не простым любопытством. Дело в том, что закон сохранения импульса p¯ выполняется для каждой его компоненты. То есть в наиболее полной форме он записывается так:
px = m * vx; py = m * vy; pz = m * vz.
Каждая компонента вектора p¯ сохраняет свое значение в системе взаимодействующих объектов, на которые не действуют внешние силы (Δp¯ = 0).
Как пользоваться этим законом и векторными представлениями величины p¯, чтобы решать задачи на взаимодействие (соударение) тел?
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Задача с двумя шарами
На рисунке ниже изображены два шара разной массы, которые летят под разными углами к горизонтальной линии. Пусть массы шаров равны m1 = 1 кг, m2 = 0,5 кг, их скорости v1= 2 м/с, v2= 3 м/с. Необходимо определить направление импульса после удара шаров, полагая последний абсолютно неупругим.
Начиная решать задачу, следует записать закон неизменности количества движения в векторной форме, то есть:
Поскольку каждая компонента импульса должна сохраняться, то нужно переписать это выражение, учитывая также, что после столкновения два шара начнут двигаться, как единый объект (абсолютно неупругий удар):
m1 * v1x + m2 * v2x = (m1 + m2) * ux;
-m1 * v1y + m2 * v2y = (m1 + m2) * uy.
Знак минус для проекции импульса первого тела на ось y появился вследствие ее направленности против выбранного вектора оси ординат (см. рис.).
Теперь нужно выразить неизвестные компоненты скорости u, а затем подставить известные значения в выражения (соответствующие проекции скоростей определяются умножением модулей векторов v1¯ и v2¯ на тригонометрические функции):
ux = (m1 * v1x + m2 * v2x) / (m1 + m2), v1x = v1 * cos(45o); v2x = v2 * cos(30o);
ux = (1 * 2 * 0,7071 + 0,5 * 3 * 0,866) / (1 + 0,5) = 1,8088 м/с;
uy = (-m1 * v1y + m2 * v2y) / (m1 + m2), v1y = v1 * sin(45o); v2y = v2 * sin(30o);
uy = (-1 * 2 * 0,7071 + 0,5 * 3 * 0,5) / (1 + 0,5) = -0,4428 м/с.
Это две компоненты скорости тела после удара и «слипания» шаров. Поскольку направление скорости совпадает с вектором импульса p¯, то ответить на вопрос задачи можно, если определить u¯. Угол его относительно горизонтальной оси будет равен арктангенсу отношения компонент uy и ux:
α = arctg(-0,4428 / 1,8088) = -13,756o.
Знак минус указывает, что импульс (скорость) после удара будет направлен вниз от оси x.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Видео:Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Видео:Урок 107. Задачи на закон сохранения импульса (ч.1)Скачать

Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Видео:Механика | кинематика на плоскости | движение по окружности | вектор угловой скоростиСкачать
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Видео:Закон изменения импульсаСкачать

Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
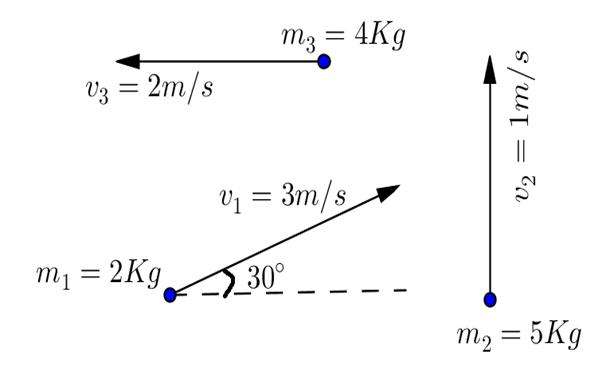
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Видео:Физика 9 класс. Движение по окружностиСкачать

Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Импульс, закон сохранения импульса
I. Импульс тела (системы тел).
1. Материальная точка равномерно движется по окружности. Как направлен импульс точки в некоторый момент времени?
1) К центру окружности.
2) По касательной к окружности.
3) От центра окружности.
4) Под некоторым углом к направлению движения в этот момент, значение угла зависит от ускорения
2. Спортивное ядро движется по траектории, изображенной на рисунке а. Как направлен вектор импульса в верхней точке траектории (рис. б)
1) 1 2) 2 3) 3 4) 4
3. 
4. Тело массой т = 1 кг движется согласно графику зависимости координаты от времени (рис.). Найдите проекцию импульса тела на ось X в момент времени t = 2 с.
5. На графике представлена зависимость проекции скорости от времени для движущегося тела массой т = 2 кг. Определите величину проекции импульса этого тела в момент времени t = 50 с.
6. На графике представлена зависимость координаты от времени для движущегося тела массой т = 2 кг. Определите величину проекции импульса этого тела в момент времени t = 5 с.
7. Пешеход массой 50 кг движется по горизонтальному участку дороги (см. рис.). Чему равен импульс пешехода и в какую сторону он направлен?
1) 0,018 кг • м/с, вправо
3) 56 кг • м/с, влево
4) 150 кг • м/с, вправо
8. Мальчик массой 50 кг бежит со скоростью 18 км/ч. Импульс мальчика равен
1) 2,8 кг·м/с 2) 10 кгм/с 3) 250 кг·м/с 4) 900 кг·м/с
9. Движение материальной точки описывается уравнением 
1) – 4 кг·м/с 2) – 2 кг·м/с 3) 4 кг·м/с 4) 6 кг·м/с
10. Тело массой 2 кг движется вдоль оси ОХ. Его координата меняется в соответствии с уравнением х = А +Bt + Ct2, где А = 2 м, В = 3 м/с, С = 5 м/с2. Чему равен импульс тела в момент времени t = 2 c?
1) 86 кг×м/с 2) 48 кг×м/с 3) 46 кг×м/с 4) 26 кг×м/с
11. Радиоуправляемый электрокар массой 50 кг движется по полигону так, что его координаты изменяются по закону: х = 2(t + t2) (см); у = 26 + 16t – 5t2 (см). Чему равен импульс электрокара к концу 4-й секунды?
12. Движение материальной точки вдоль оси X происходит по закону х = 10 + 4t — 2t2 (м). Координата, в которой импульс точки обращается в нуль, равна:
1) 1,2м 2) 5 м 3) 6 м 4) 12 м
13. Если тело, брошенное со скоростью 10 м/с под углом 600 к горизонту, в высшей точке траектории имеет импульс, модуль которого равен 10 кг·м/с, то какова масса этого тела?
1) 0,5 кг 2) 1 кг 3) 2 кг 4) 5 кг
14. С балкона высотой 20 м на поверхность Земли упал мяч массой 0,2 кг. Из-за сопротивления воздуха скорость мяча у поверхности Земли оказалась на 20 % меньше скорости тела, свободно падающего с высоты 20 м. Импульс мяча в момент падения равен
1) 4 кг·м/c 2) 4,2 кг·м/с 3) 3,2 кг·м/с 4) 6,4 кг·м/с
15. Металлический шарик, падая с высоты 1 м на стальную плиту, отскакивает от неё на высоту 0,49 м. Во сколько раз уменьшается импульс шарика при ударе?
1) импульс не меняется 2) в 1,23 3) в 2,04 4) в 1,5
16. Два шарика, стальной и алюминиевый, одинакового объема падают с одной и той же высоты. Сравните их импульсы в момент соприкосновения с землей. Силой сопротивления воздуха пренебречь.
1) импульс стального шара больше импульса алюминиевого
2) импульс стального шара меньше импульса алюминиевого
3) импульсы обоих шаров равны
4) импульсы обоих шаров равны 0
17. Отношение массы грузовика к массе легкового автомобиля 

18. Легковой автомобиль и грузовик движутся со скоростями v1 = 108 км/ч и v2 = 54 км/ч. Масса автомобиля т = 1000 кг. Какова масса грузовика, если отношение импульса грузовика к импульсу автомобиля равно 1,5?
1) 3000 кг 2) 4500 кг 3) 1500 кг 4) 1000 кг
19. 




20. Тело, двигаясь с постоянной по модулю скоростью, повернулось по дуге окружности на 90° (рис.). Какое направление имеет вектор изменения импульса Δ 
21. Два тела с массами, равными 1 и 2 кг, движутся равномерно во взаимно перпендикулярных направлениях со скоростями 3 и 2 м/с соответственно. Определить импульс данной системы тел.
1) 5 кг·м/с 2) 9 кг·м/с 3) 1 кг·м/c 4) 0
22. Материальная точка массой m = 100 г движется по окружности с постоянной по модулю скоростью v = 10 м/с. Определите модуль изменения импульса за одну четверть периода.
1) 1 кг·м/с 2) 0,7 кг·м/с 3) 2 кг·м/с 4) 1,4 кг·м/с
23. Мяч массой 200 г вертикально падает на горизонтальную плиту со скоростью 10 м/с и отскакивает вверх с такой же скоростью. Изменение импульса мяча равно
1) 0 2) 2 кг·м/с 3) 4 кг·м/с 4) 2000 кг·м/с
24. Теннисный мяч массы m = 200 г движется со скоростью v = 12 м/с, составляющей угол 600 с перпендикуляром к стенке, и упруго ударяется о неподвижную стенку. Определите модуль изменения импульса мяча?
1) 0 2) 1,2 кг м/с 3) 2,4 кг м/с 4) 24 кг м/с
25. Мяч абсолютно упруго ударяется о горизонтальную плиту. При ударе импульс мяча меняется на Δ

3) под углом 60° к вертикали
4) под углом 30° к вертикали
26. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90°. Импульс шайбы перед ударом равен 1 кг·м/с. Чему равен модуль изменения импульса шайбы в результате удара?
1) 0 2) 1кг·м/с 3) 
27. Скорость материальной точки массой 1 кг при прямолинейном движении изменяется по закону vx = 5 + 0,5t (м/с). Через сколько секунд после начала движения импульс точки изменится на Δр = 4 кг • м/с?
1) Импульс точки не изменится.
III. Закон сохранения импульса.
28. Тело свободно падает на Землю. Изменяются ли при падении тела импульс тела, импульс Земли и суммарный импульс системы «тело–Земля», если считать эту систему замкнутой?
1) импульс тела, импульс Земли и импульс системы «тело–Земля» не изменяются
2) импульс тела изменяется, а импульс Земли и импульс системы «тело–Земля» не изменяются
3) импульс тела и импульс Земли изменяются, а импульс системы «тело–Земля» не изменяется
4) для ответа недостаточно данных
29. 
1) Тележка 1 двигалась впереди и имела большую массу.
2) Тележка 1 двигалась впереди и имела меньшую массу.
3) Тележка 2 двигалась впереди и имела большую массу.
4) Тележка 2 двигалась впереди и имела меньшую массу.
30. Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 3·10-2 кг·м/с и 4·10-2 кг·м/с. Столкнувшись, шарики слипаются. Импульс слипшихся шариков равен
1) 10-2 кг·м/с 2) 3,5·10-2 кг·м/с 3) 5· 10-2 кг·м/c 4) 7· 10-2 кг·м/с
31. Тележка массой m, движущаяся со скоростью v, сталкивается с неподвижной тележкой той же массы и сцепляется с ней. Импульс тележек после взаимодействия равен
32. С неподвижной лодки массой 50 кг на берег прыгнул мальчик массой 40 кг со скоростью 1 м/с, направленной горизонтально. Какую скорость относительно берега приобрела лодка?
1) 0,2 м/с 2) 0,8 м/с 3) 1 м/с 4) 1,8 м/с
33. 
1) 0,2 м/с 2) 0,6 м/с 3) 0,5 м/с 4) 0,3 м/с
34. Два тела массами 3 кг и 2 кг, двигавшиеся навстречу друг другу со скоростями 2 м/с и 3 м/с, после неупругого удара:
1) будут двигаться вправо со скоростью 2 м/с
2) будут двигаться вправо со скоростью 1 м/с
4) будут двигаться влево со скоростью 1 м/c
35. Железнодорожная платформа с закрепленным на ней орудием суммарной массой 20 т движется со скоростью 2,5 м/с. Из орудия выпущен снаряд массой 25 кг в направлении движения платформы со скоростью 700 м/с относительно Земли. Скорость платформы (относительно Земли) после выстрела равна
1) 0,8 м/с 2) 1,2 м/с 3) 1,6 м/с 4) 2 м/с
36. Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле 300 м/с. Какова скорость охотника после выстрела?
1) 0,1 м/с 2) 0,15 м/с 3) 0,3 м/с 4) 3 м/с
37. Два тела, летящие навстречу друг другу со скоростями 5 м/с каждое, после абсолютно неупругого удара стали двигаться как единое целое со скоростью 2,5 м/с. Каково отношение масс этих тел?
1) 1 2) 1,5 3) 2 4) 3
38. Две тележки движутся вдоль одной прямой в одном направлении. Массы тележек m и 2m, скорости – соответственно 2v и v. Какой будет скорость тела после абсолютно неупругого столкновения?
39. Тележка массой m движется со скоростью 3v и догоняет тележку массой 3m, движущуюся в ту же сторону со скоростью v. Каков модуль скорости тележек после их абсолютно неупругого столкновения?
1) 



40. 
1) 1 2) 2 3) 3 4) 4
41. 
1) 


42. 
1) 


43. Перед столкновением два мяча движутся взаимно перпендикулярно, первый — с импульсом р1 = 3 кг·м/с, а второй — с импульсом р2 = 4 кг· м/с. Чему равен модуль импульса системы мячей сразу после столкновения? Время столкновения считать малым, а столкновение — абсолютно упругим.
44. На неподвижный бильярдный шар налетел другой такой же шар. После удара шары разлетелись под углом 90o так, что импульс одного равен р1= 0,3 кг·м/с, а другого р2 = 0,4 кг·м/с. Налетающий шар имел импульс, равный:
1) 0,1 кг·м/с 2) 0,5 кг·м/с 3) 0,7 кг·м/с 4) 0,25 кг·м/с
45. 
1) 2 кг·м/с 2) 2,5 кг·м/с 3) 3,5 кг·м/с 4) 4 кг·м/с
46. При произвольном делении покоившегося ядра химического элемента образовалось три осколка массами: 3m; 4,5m; 5m. Скорости первых двух взаимно перпендикулярны, а их модули равны соответственно 4 v и 2v. Определите модуль скорости третьего осколка
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ДЛЯ НЕЗАМКНУТЫХ СИСТЕМ
47. Закон сохранения импульса для незамкнутой механической системы можно применять в случаях:
A. когда внешние силы много меньше сил взаимодействия между телами внутри системы;
Б. когда внешние силы действуют, но их векторная сумма равна нулю;
B. когда время взаимодействия между телами системы велико.
48. На тело массой т действуют силы, как показано на рисунке. Закон сохранения импульса будет выполняться в проекции на ось:
4) Вообще выполняться не будет
49. Если на вагонетку массой m, движущуюся по горизонтальным рельсам со скоростью v, сверху вертикально опустить груз, масса которого равна половине массы вагонетки, то скорость вагонетки с грузом станет равной
50. Мальчик массой 50 кг, стоя на очень гладком льду, бросает груз массой 8 кг под углом 60о к горизонту со скоростью 5 м/с. Какую скорость приобретет мальчик?
1) 5,8 м/с 2) 1,36 м/с 3) 0,8 м/с 4) 0,4 м/с
51. Шар массой 200 г движется со скоростью 10 м/с под углом 45° к горизонту к стоящей на горизонтальной площадке платформе с песком массой 20 кг. Какой импульс приобретет после удара платформа с шаром? Считать, что платформа может горизонтально двигаться без трения.
1) 0 кг·м/с 2) 2 кг·м/с 3) 4 кг·м/с 4) 1,4 кг·м/с
52. Камень массой m1 = 4 кг падает под углом 60° к горизонту со скоростью 10 м/с в тележку с песком, покоящуюся на горизонтальных рельсах (см. рисунок). Импульс тележки с песком и камнем после падения камня равен

53. При выстреле из пушки, находящейся на гладкой поверхности, вылетает снаряд под углом 300 к горизонту. За счет отдачи пушка откатывается назад со скоростью 3 м/с. Если импульс снаряда сразу после выстрела 1039 кг м/с, то масса пушки равна
1) 200 кг 2) 300 кг 3) 400 кг 4) 500 кг 5) 1000 кг
54. При выстреле из пушки, находящейся на гладкой поверхности, вылетает снаряд под углом 300 к горизонту. За счет отдачи пушка откатывается назад со скоростью v = 2 м/с. Если масса пушки равна 500 кг, то импульс системы (пушка+снаряд) сразу после выстрела равен
1) 0 2) 156 кг·м/с 3) 578 кг·м/с 4) 1000 кг·м/с
IV. Закон изменения импульса
55. Тело массой 3 кг движется прямолинейно под действием постоянной силы, равной по модулю 5 Н. Определите модуль изменения импульса тела за 6 с.
1) 30 кг×м/с 2) 20 кг×м/с 3) 15 кг×м/с 4) 10 кг×м/с
56. Тело движется по прямой в одном направлении под действием постоянной силы, равной по модулю 8 Н. Импульс тела изменился на 40 кг×м/с. Сколько времени потребовалось для этого?
1) 0,5 с 2) 5 с 3) 48 с 4) 320 с
57. Тело движется по прямой в одном направлении в инерциальной системе отсчета. Под действием постоянной за 3 с импульс тела изменился на 6 кг·м/с. Каков модуль силы?
1) 0,5 Н 2) 2 Н 3) 9 Н 4) 18 Н
58. Молоток массой 0,8 кг ударяет по небольшому гвоздю и забивает его в доску. Скорость молотка в момент удара равна 5 м/с, продолжительность удара равна 0,2 с. Средняя сила удара молотка равна:
1) 80 Н 2) 40 Н 3) 20 Н 4) 8 Н
59. 
60. На рисунке показан график изменения импульса тележки с течением времени в инерциальной системе отсчета. Какой из приведенных ниже графиков показывает изменение с течением времени суммарной силы, действующей на эту тележку?
💡 Видео
закон сохранения импульса. #физика #анимация #егэ #лодкаСкачать

Центростремительное ускорение. 9 класс.Скачать

Урок 89. Движение по окружности (ч.1)Скачать