Вектор и скаляр отличие

Видео:Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Разница между скалярным и векторным

Главное отличие

Основное различие между скаляром и вектором состоит в том, что скаляр известен как величина, которая включает единственную величину и не имеет направления, тогда как вектор известен как физическая величина, которая состоит из направления и величины.

Скаляр против вектора

Скаляр содержит только величину и не имеет направления; с другой стороны, вектор также содержит как величину, так и направление. Вектор состоит из единственного измерения и считается одномерным; Напротив, вектор содержит множество измерений, поэтому он считается многомерным.

Скалярная величина изменяется, когда происходит изменение ее величины; с другой стороны, векторная величина меняется, когда изменяется величина или направление. Стандартные правила алгебры применимы в случае скаляра; в то же время в векторной алгебре соблюдаются различные наборы алгебраических правил, известных как векторная алгебра.

Одна скалярная величина может быть разделена с другой скалярной величиной; с другой стороны, одну векторную величину нельзя разделить с другой векторной величиной. Сравнение двух скалярных чисел относительно просто; напротив, корреляция между двумя векторными величинами сравнительно сложна.

Скаляр может быть представлен единицей и величиной (числом); с другой стороны, векторная величина может быть представлена ​​единицей и величиной (числом), направлением с помощью ограничения единицы измерения или с помощью стрелки вверху. Символ скаляра — это символ количества; однако, напротив, символ вектора — это символ количества и знак стрелки вверху.

Некоторыми примерами скалярной величины являются энергия, масса, длина, температура и плотность, а некоторыми случаями вектора являются ускорение, вес, смещение, сила и скорость.

Сравнительная таблица

Что такое скаляр?

Вид физической величины, в которой размерность определяется только величиной величины, а не направлением, тогда это называется скаляром. Скалярная величина никогда не состоит из направления, потому что она касается только величины объекта.

В сценарии скаляра, когда замечается какое-либо изменение количества, это происходит только из-за изменения его величины. Как правило, скалярные величины подчиняются общим законам алгебраических правил, и поэтому их можно легко алгебраически вычесть, сложить, разделить или умножить, как и стандартные числа, хотя скалярные величины должны содержать точные единицы.

Что такое вектор?

Величина, в которой размер определяется направлением и величиной объекта, обычно называется вектором. Когда две величины имеют одинаковую величину и одинаковое направление, тогда эти две величины будут называться векторными величинами.

Когда чередование происходит как по величине, так и по направлению, это приведет к изменению векторной величины. Векторная величина обычно не следует основным правилам алгебры, потому что направление связано с векторной величиной, вместо этого следует алгебраическим векторным законам. Некоторые примеры Vector: ускорение, вес, смещение, сила и скорость.

Ключевые отличия

1. Сумма, которая состоит только из величины, но не имеет направления, называется скаляром; С другой стороны, величина, которая включает как направление величины, так и величину, также известна как вектор.
2. Каждая скалярная величина считается одномерной, потому что она состоит только из одного измерения; напротив, векторная величина считается многомерной, потому что она состоит из одного, двух или трех измерений.
3. Когда происходит какое-либо изменение величины скалярной величины, скалярная величина также будет изменена; с другой стороны, при любом изменении направления или величины векторной величины вектор также будет изменен.
4. Скалярное число не может быть разрешено ни в каком направлении, потому что оно всегда состоит из одного и того же значения, несмотря на направление; Напротив, векторная величина может быть определена в любом направлении с помощью синуса или косинуса любого соседнего угла.
5. Когда математическое выражение находится между двумя скалярными числами, ответ будет скаляром; однако, когда математическое выражение используется между скалярной и векторной величиной, результатом всегда будет вектор. С другой стороны, когда математическая операция выполняется между двумя векторами, результатом всегда будет вектор или, возможно, скаляр, например, умножение точек между двумя векторами обычно приводит к скаляру. Напротив, суммирование, вычитание или перекрестное умножение дает только вектор.
6. Несколько примеров скалярной величины — это энергия, масса, длина, температура и плотность, а некоторыми примерами вектора являются ускорение, вес, смещение, сила и скорость.

Заключение

Из приведенного выше обсуждения делается вывод, что если величина состоит только из величины, то она будет известна как скалярная величина; Напротив, если величина состоит как из направления, так и из величины, то это будет векторная величина.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Скалярные и векторные величины, основные определения.Скачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Физика | Ликбез по векторамСкачать

Что такое вектор

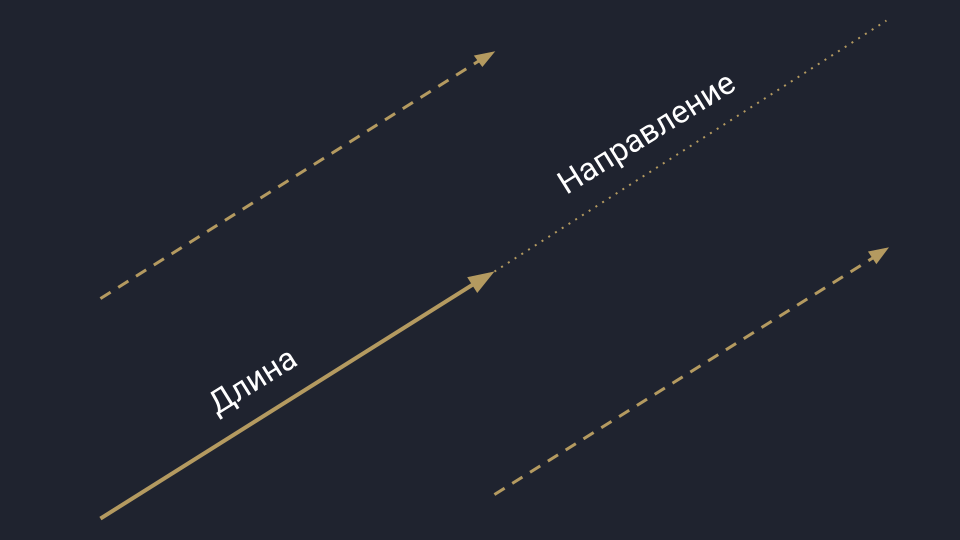
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

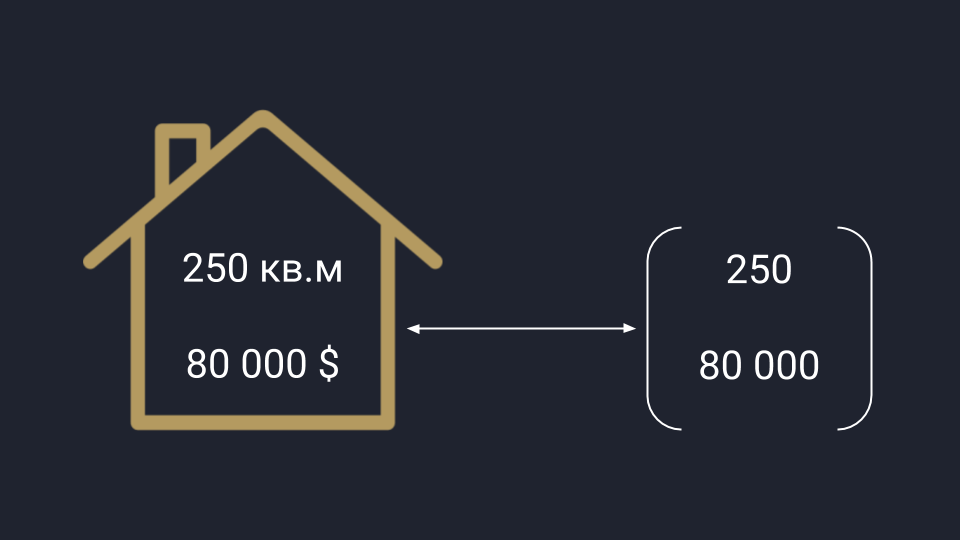
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

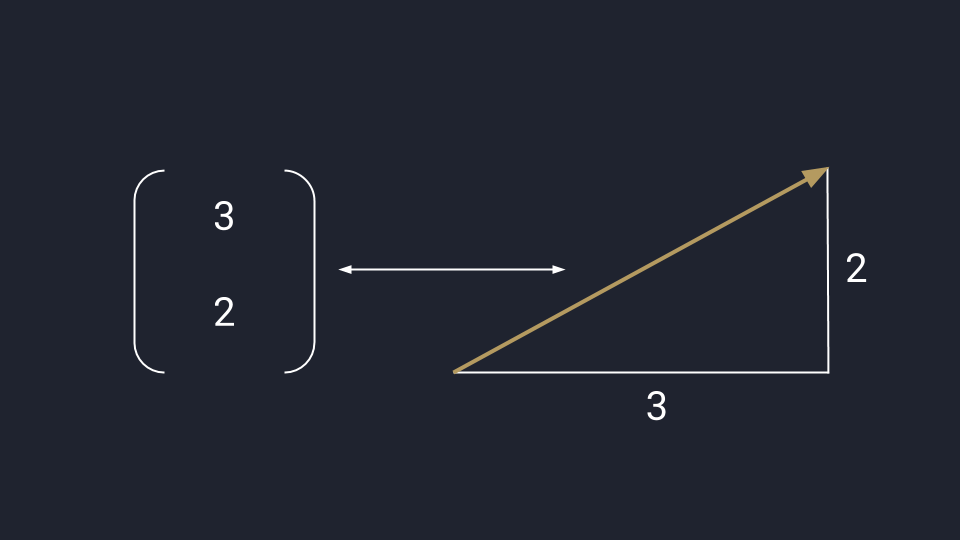
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

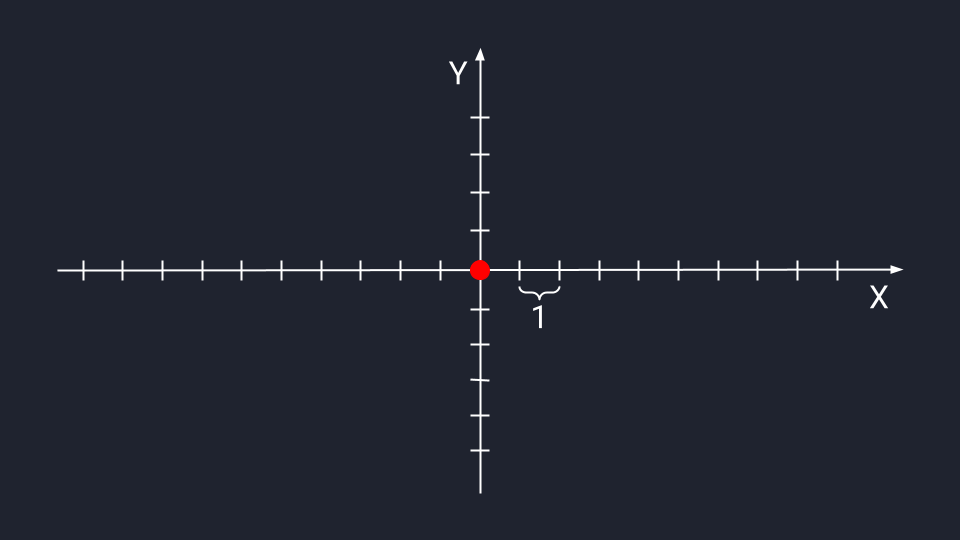
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

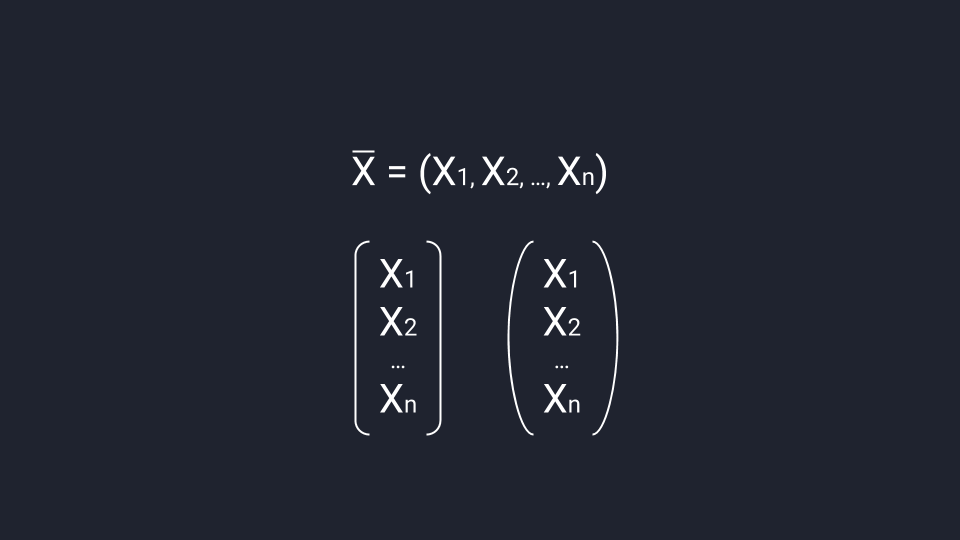
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

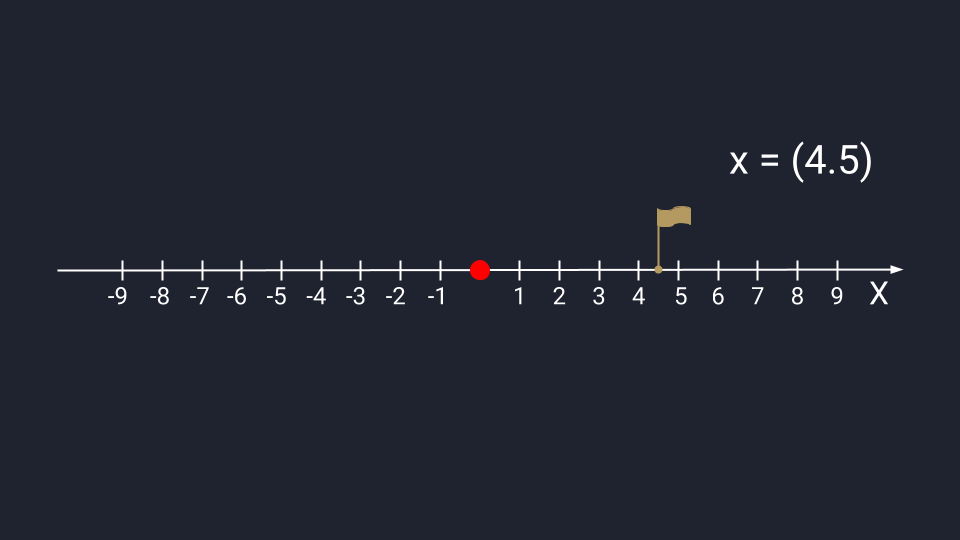
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

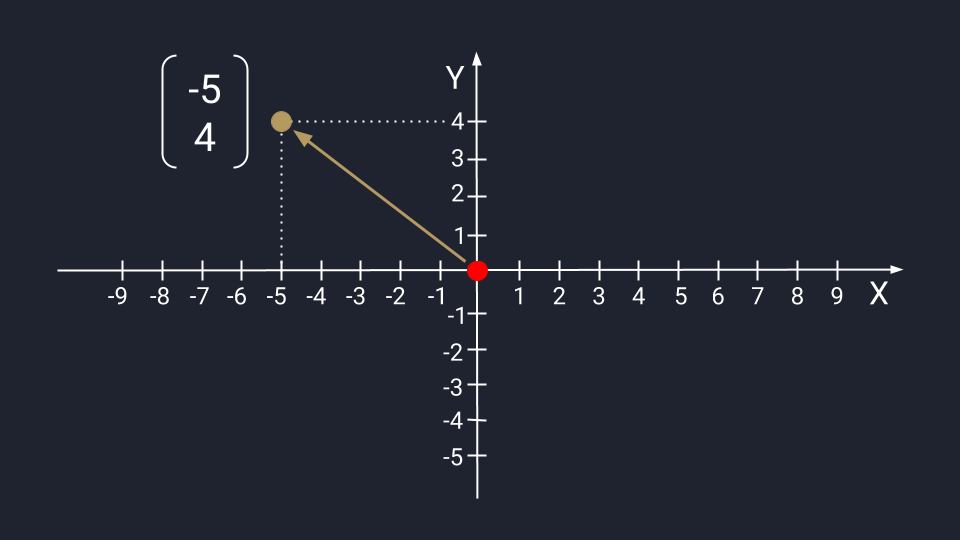
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

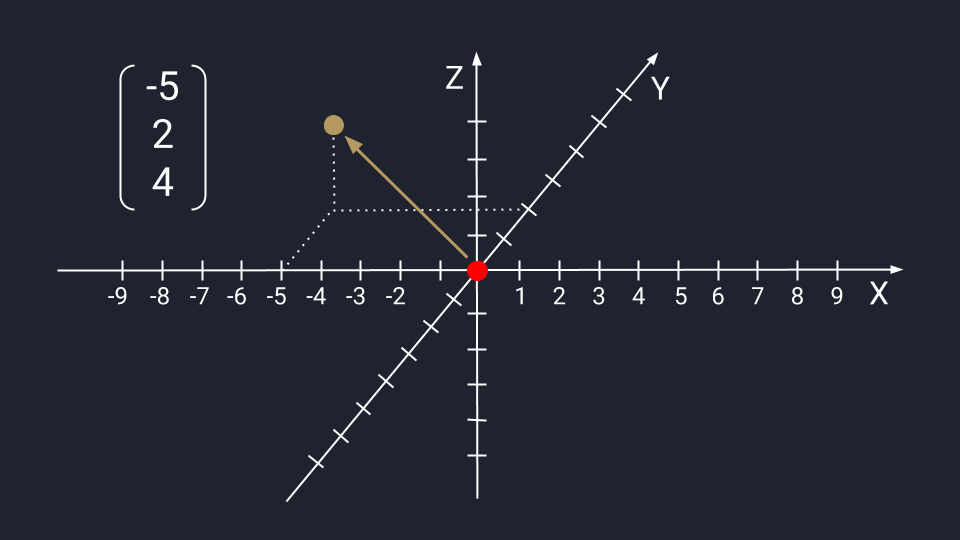
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Скалярное произведение векторов. 9 класс.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Физика. Объяснение темы "Векторные и скалярные величины"Скачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Какая разница между вектором и скаляром?

Часто многим ученикам или даже студентам сложно понять отличия векторной и скалярной величины. Поэтому я хотел бы объяснить максимально понятным языком суть каждого из этих понятий и на примерах показать главные их отличия. Так как они оба часто используются в математических задачах, для правильного и быстрого решения которых нужно знать это.

Начнём с определений:

Векторной величиной, или вектором (в широком смысле), называется всякая величина, обладающая направлением.
Скалярной величиной, или скаляром, называется величина, не обладающая направлением.

То есть у вас уже должна появиться основная картина, если есть направление у величины, то это вектор, а если нет, то это скаляр. Далее рассмотрим всё на конкретных примерах.

Пример 1. Когда какая-то сила действует на материальную точку, то она будет вектором, так как она обладает направлением. Так же и скорость материальной точки — тоже вектор.

Пример 2. А от уже температура тела будет скаляром, так как с ней не связано никакое направление. Поэтому масса тела и его плотность — тоже будут скалярами.

Если не учитывать направление векторной величины, то ее, как и скалярную, можно измерить, выбрав соответствующую единицу измерения. Но в этом случае полученное число, характеризует скалярную величину полностью, а векторную только частично. Её можно полностью охарактеризовать направленным отрезком, предварительно задав линейный масштаб. И это хорошо показано в следующем примере.
Пример 3. Направленный отрезок АВ при введенном масштабе MN, изображающем единицу силы (1 Н) (более подробно смотрите на рисунке), характеризует силу в 3,5 Н, направление которой совпадает с направлением отрезка АВ (указанным стрелкой).

Думаю, после таких явных данных у вас уже не должно появиться проблем, при различии этих понятий.

📸 Видео

Математика без Ху!ни. Свойства скалярного и векторного произведений.Скачать

Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Угол между векторами. 9 класс.Скачать

Скалярные произведения и дуальность | Сущность Линейной Алгебры, глава 7Скачать

ОЧЕНЬ ВАЖНЫЙ УРОК. РАЗНИЦА МЕЖДУ ВЕКТОРНОЙ И РАСТРОВОЙ ГРАФИКОЙ. СРАВНИВАЕМ. ДОСТУПНО И БЕЗ ВОДЫСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

векторное скалярноеСкачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать