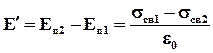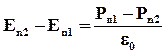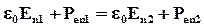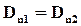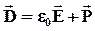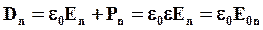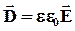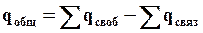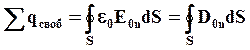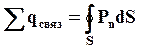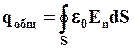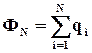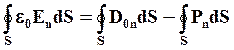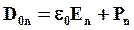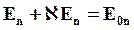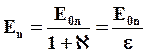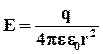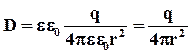Источником электростатического поля являются свободные и связанные электрические заряды: линии напряженности начинаются на положительных зарядах (или в бесконечности) и оканчиваются на отрицательных (или в бесконечности).
Однако при решении задач, связанных с электрическим полем в диэлектрике, в ряде случае оказывается более удобным учитывать только поле свободных зарядов. Для этого вводится понятие вектора электрического смещения ( 
Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2.
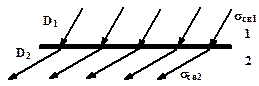 | В первом диэлектрике напряженность электрического поля и вектор поляризации соответственно равны 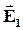 и и 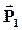 , во втором диэлектрике — , во втором диэлектрике — 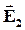 и и 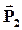 . . |
В общем случае все эти четыре вектора произвольно ориентированы в диэлектриках, поэтому можно говорить об их тангенциальных к границе раздела (Et1, Et2 и Pt1, Pt2) и нормальных (En1, En2 и Pn1, Pn2) составляющих.
На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых равны sсв1 и sсв2. Эти заряды создадут электрическое полеE’. Напряженность E’ уменьшит нормальную составляющую напряженности в одном диэлектрике и увеличит в другом, поэтому E’будет определятьсяразностью нормальных составляющих напряженности:
Это уравнение можно записать так:
Отсюда видно, что на границе двух диэлектриков сохраняется нормальная составляющая:
Это и есть вектор электрического смещения.
Т.е. можно говорить о линиях электрического смещения и о потоке вектора электрического смещения через некоторую поверхность.
Поток вектора электрического смещения не изменятся на границе двух диэлектриков, т.е. линии этого вектора не начинаются и не заканчиваются на связанных зарядах, а линии напряженности поля начинаются и заканчиваются на связанных зарядах.
Из приведенных соотношений видно,
Внутри диэлектрика 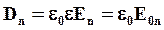
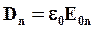
Видно, что величина Dn остается постоянной при переходе из вакуума в среду, а величина En изменяется.
Или в векторной форме:
Запишем для нашего случая теорему Гаусса. Общий заряд в диэлектрике qобщ можно найти как разность свободных зарядов и связанных зарядов.
Сумма 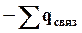
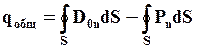
отсюда получаем:
Величина поля внутри диэлектрика:
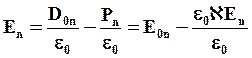
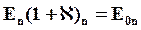
В других конкретных случаях соотношения для электростатического поля с диэлектриком имеют другой вид и чаще всего значительно более сложный, нежели полученные нами для плоской пластины внутри конденсатора. В частности, в некоторых случаях введение диэлектрика сопровождается не только ослаблением поля, но и его усилением.
 | Поле, созданное зарядом q в т. A и B, по направлению совпадает с полем связанных зарядов диэлектрика M, внесенного в поле заряда q. |
В т. C величины E0 и E’ направлены в противоположные стороны, т.е. в этой точке внесение диэлектрика сопровождается ослаблением поля.
Напряженность электрического поля точечного заряда q в диэлектрике выражается формулой:
Получаем выражение для электрического смещения поля точечного заряда:
Как видно, электрическое смещение в однородном изотропном диэлектрике не зависит от свойств вещества.
- Теорема Гаусса для поля в диэлектрике. Явления на границе раздела двух диэлектриков. Преломление линий смещения и напряженности
- Преломление линий поляризации на границе двух диэлектриков
- Закон преломления линий поля на границе двух диэлектриков
- Готовые работы на аналогичную тему
- Закон преломления линий электрического смещения
- 📺 Видео
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Теорема Гаусса для поля в диэлектрике. Явления на границе раздела двух диэлектриков. Преломление линий смещения и напряженности
Запишем теперь теорему Гаусса для поля в диэлектрике через поток вектора электрического смещения D = ге()Е. Из формулы (16.8) имеем с учетом ослабления поля в диэлектрике в случае среды с диэлектрической проницаемостью е
Таким образом, если мы записываем теорему Гаусса через поток вектора электрического смещения, то необходимо учитывать только свободные заряды — без учета свойств диэлектрика. В свою очередь, при записи теоремы Гаусса через поток вектора напряженности мы учитываем свойства диэлектрика как со свободными, так и со связанными зарядами. Аналогичны различия в картинах силовых линий напряженности и электрического смещения. Силовые линии напряженности начинаются и заканчиваются как на свободных, так и на связанных зарядах. А силовые линии электрического смещения начинаются и заканчиваются только на свободных зарядах.
Подобные рассуждения позволяют решить задачу о преломлении линий смещения и напряженности на границе раздела двух диэлектриков. Будем считать, что на этой границе отсутствуют свободные заряды. Однако, как мы уже видели (см. рис. 19.2), на границе диэлектрика (а в общем случае — на границе раздела двух диэлектриков) в поле возникает связанный заряд, который может приводить к разрыву полей.
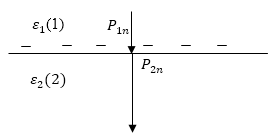
Рассмотрим сначала соотношение между нормальными к поверхности раздела компонентами вектора электрического смещения Dn. Воспользуемся теоремой Гаусса, выбрав в качестве гауссовой поверхности поверхность цилиндра (рис. 19.3). При этом основания цилиндра должны быть малы (чтобы считать электрическое смещение константой), параллельны границе раздела и находиться в разных диэлектриках, а высота цилиндра должна быть бесконечно малой — в том числе и по сравнению с основаниями. Такой выбор позволяет пренебречь потоком вектора электрического смещения через боковую поверхность цилиндра по сравнению с потоком через основания.
Тогда из теоремы Гаусса (19.11) следует, что потоки вектора электрического смещения через основания равны по модулю, причем один направлен наружу цилиндра, другой — внутрь. Геометрически это означает, что потоки направлены в одну сторону: = Д,25. Поскольку площади оснований
цилиндра S равны, то получаем, что нормальная компонента вектора электрического смещения на границе раздела диэлектриков остается непрерывной’.
Выразив полученное соотношение через напряженность поля, получим, что нормальная компонента вектора напряженности на границе раздела диэлектриков претерпевает разрыв:
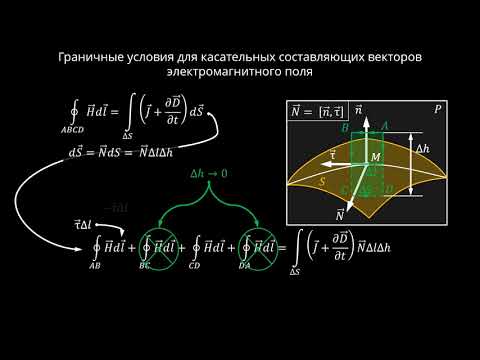
Перейдем теперь к тангенциальным составляющим, соотношение которых удобно найти для вектора напряженности с помощью теоремы о циркуляции (заметим, что, очевидно, теорема о циркуляции остается справедливой и в диэлектрике).
Выделим вблизи границы раздела небольшой прямоугольный контур ABCD (рис. 19.4). Выберем стороны АВ = CD = I так, что они параллельны границе раздела и находятся в разных диэлектриках, а стороны ВС и DA бесконечно малы но сравнению со сторонами А В и CD. Тогда, пренебрегая в теореме о циркуляции (17.7) интегралами по бесконечно малым сторонам, получим: Ех<1 — Ех21 = 0, откуда следует, что тангенциальная компонента вектора напряжен
ности на границе раздела диэлектриков остается непрерывной’.
Выразив это соотношение через электрическое смещение, получим, что тангенциальная компонента вектора электрического смещения на границе раздела диэлектриков претерпевает разрыв:

Таким образом, мы получили, что векторы напряженности и электрического смещения претерпевают преломление при переходе из одной среды в другую.
Пусть в первой среде (рис. 19.5) tga, = гг, а во вто-
рой среде tga2 = —. Тогда из формул (19.13)
и (19.14) получим закон преломления вектора напряженности электрического поля
Аналогично преломляются и силовые линии электрического смещения. Формула показывает, что при переходе в диэлектрик с большей диэлектрической проницаемостью силовые линии напряженности и электрического смещения удаляются от нормали.
Видео:45. Электрическое смещениеСкачать

Преломление линий поляризации на границе двух диэлектриков
Вы будете перенаправлены на Автор24
При переходе через границу двух различных диэлектриков можно записать следующее выражение:
где $P_$-нормальная составляющая вектора поляризации диэлектрика с номером 2, $P_$ — нормальная составляющая вектора поляризации диэлектрика с номером 1. Для определенности будем считать, что $_2>_1$, а вектор напряженности направлен из первой среды во вторую. В качестве положительной выберем нормаль, которая направлена во вторую среду. Тогда величины $P_, P_$- положительные, а связанный заряд будет отрицательным. Поведение нормальной составляющей вектора поляризации можно изобразить рис.1. Причем из (1) и того, что $у_
Напомним, что в изотропном диэлектрике связь между поляризованность и напряженностью для большого класса диэлектриков и широкого круга явлений линейна и однородна, то есть:
где $varkappa $ — диэлектрическая восприимчивость (безразмерная величина), уравнение записано в системе СИ. Вектор поляризации направлен в таком случае либо также как вектор $overrightarrow$ или в противоположном направлении. Следовательно, тангенциальная составляющая вектор поляризованности будет вести себя так же как тангенциальная составляющая вектора напряженности, поведение которой мы рассмотрим чуть дальше.
Видео:Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Закон преломления линий поля на границе двух диэлектриков
Пусть на границе раздела двух диэлектриков нет свободных зарядов. В таком случае мы можем записать, что для нормальной составляющей вектора напряженности ($E_n$) выполняется равенство:
Для тангенциальной составляющей ($E_$) мы имеем:
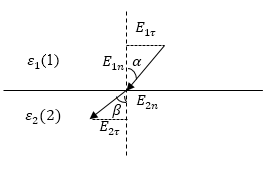
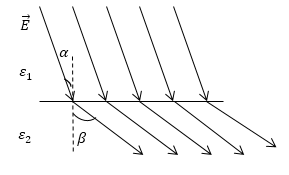
В том случае, если $_2>_1$, тогда $E_>E_$, тогда силовые линии можно изобразить так, как показано на рис. 2.
Готовые работы на аналогичную тему
На рис.2 видно, что силовые линии удаляются от нормали, если переход происходит из диэлектрика с меньшей диэлектрической проницаемостью в диэлектрик с большей диэлектрической проницаемостью. При чем, из того же рисунка очевидно соотношение:
где $alpha $- угол между нормалью к границе раздела двух диэлектриков и направлением вектора напряженности поля в первой среде. Кроме того, можно записать, что:
где $beta $- угол между нормалью к среде раздела двух диэлектриков и направлением вектора напряженности во второй среде. Разделим выражение (3) на (4), получим:
Используем соотношения (1) и (2), получим:
Уравнение (8) называют законом преломления линий поля на границе двух диэлектриков.
Видео:Билет №02 "Теорема Гаусса"Скачать

Закон преломления линий электрического смещения
На границе диэлектриков линии электрического смещения терпят преломление, угол между нормалью к поверхности раздела и линией электрического смещения изменяется ($alpha to beta $). Аналогично, как для вектора напряженности, легко получить:
А мы знаем, что на границе двух диэлектриков выполняются следующие условия:
следовательно, подставляя граничные условия для составляющих вектора смещения в (9) получим закон преломления линий электрического смещения:
Сравним (11) и (7), можем записать:
Для углов падения и преломления получим:
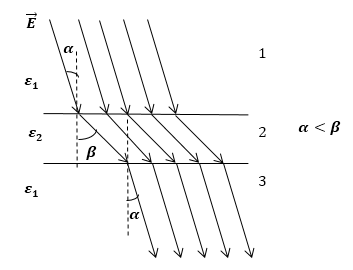
Задание: На рис. 3 изображена картина линий вектора $overrightarrow $при переходе их одного диэлектрика ($_1$) в другой ($_2$). Какая из диэлектрических проницаемостей среды больше?
Рассмотрим, как ведут себя силовые линии при прохождении через границу раздела двух диэлектриков. При переходе через границу раздела двух диэлектриков, если отсутствуют свободные заряды выполняется условие:
Это означает, что в диэлектрике с большей диэлектрической проницаемостью, вектор напряженности составляет больший угол с нормалью к границе раздела двух диэлектриков.
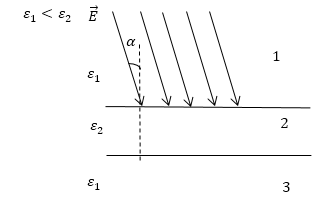
Задание: Диэлектрическая пластина внесена в однородное электрическое поле (рис.4), изобразите силовые линии поля в области 2, 3. Учесть, что $_1
При переходе из диэлектрика с меньшей плотностью ($_1)$ в диэлектрик с большей плотностью($_2$) силовые линии поля отклоняются от нормали к границе раздела диэлектриков на больший угол ($alpha
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 12 2022
📺 Видео
Диэлектрик в электрическом полеСкачать

Диэлектрики в электрическом поле. 10 класс.Скачать

Билет №06-08 "Диэлектрики"Скачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Диэлектрики в электростатическом поле. Поляризация диэлектриков | Физика 10 класс #48 | ИнфоурокСкачать

Билет №31 "Ток смещения"Скачать

46. Граничные условия для электрического поляСкачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Поляризация диэлектрикаСкачать

Лекция 237. Вектор электрической индукцииСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

2.5 Граничные условия для векторов поля на поверхности раздела средСкачать
Диэлектрики в электрическом полеСкачать

Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Урок 222. Поток вектора напряженности электрического поляСкачать

Лекция 4 -1 Поляризация диэлектриковСкачать