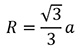Основные определения и свойства призм. Теорема Эйлера Основные определения и свойства призм. Теорема Эйлера |
 Виды призм. Прямые и наклонные призмы. Правильные призмы Виды призм. Прямые и наклонные призмы. Правильные призмы |
 Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды |
- Основные определения и свойства призм. Теорема Эйлера
- Виды призм. Прямые и наклонные призмы. Правильные призмы
- Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды
- Треугольная призма все формулы и примеры задач
- Определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Пример призмы
- Задачи на расчет треугольной призмы
- Правильная треугольная призма
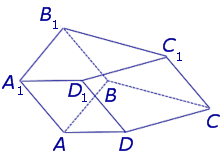
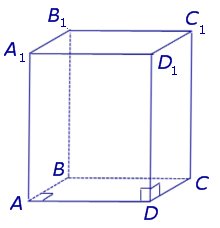
- Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
- Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.
- 🎥 Видео
Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

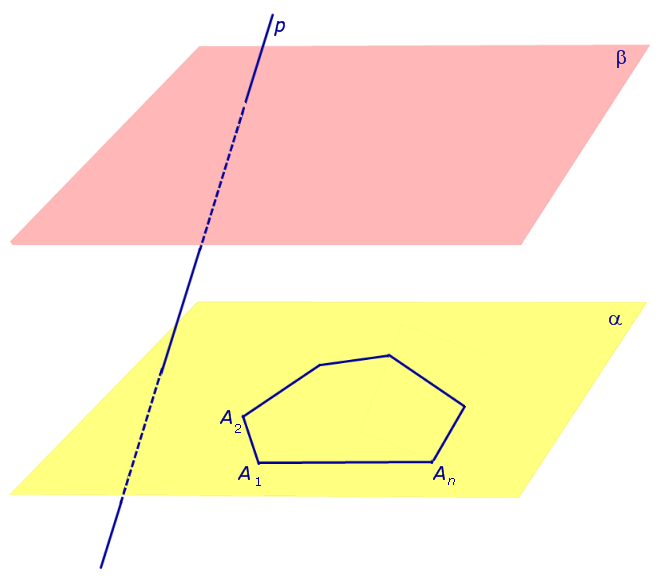
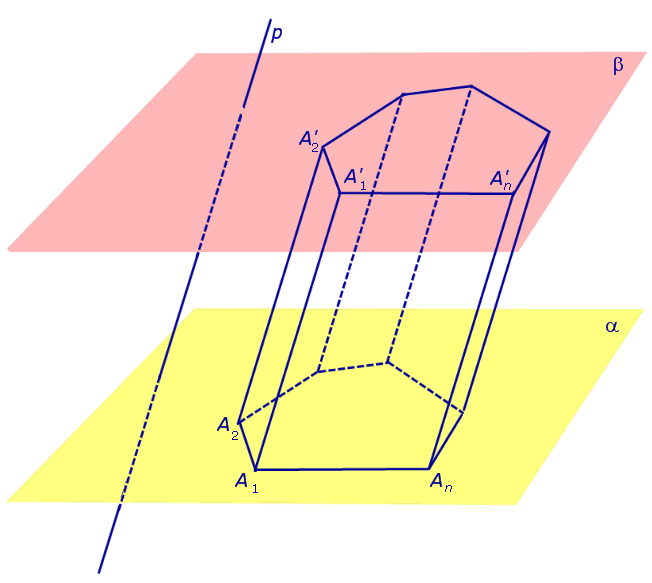
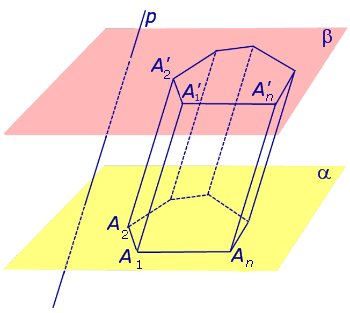
Основные определения и свойства призм. Теорема Эйлера
Утверждение 1. Каждый из n четырехугольников
Для остальных четырехугольников доказательство проводится аналогично.
называют боковыми гранями призмы . Совокупность всех боковых граней призмы составляет боковую поверхность призмы .
Утверждение 2 . Все боковые ребра призмы равны.
Это утверждение непосредственно вытекает из утверждения 1.
Замечание 1. В случае, когда не требуется делать специальных уточнений,
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
| + |
| – |
| = | 2 |
| + |
| – |
| = | 2 |
| + |
| – |
| – |
| = | 2 |
Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
то теорема Эйлера доказана.
Определение 7. Расстояние между плоскостями Расстояние между плоскостями , на которых лежат основания призмы, называют высотой призмы.
Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
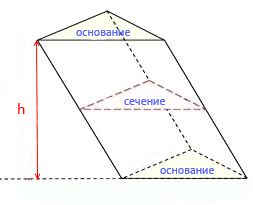
Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
Видео:ЕГЭ-2020 по математике: площадь боковой поверхности треугольной призмыСкачать

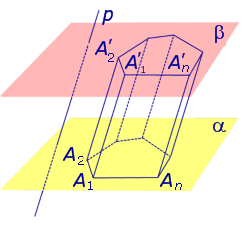
Виды призм. Прямые и наклонные призмы. Правильные призмы
Существует следующая классификация призм.
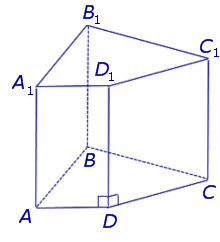
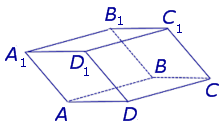
Определение 8. Прямой призмой называют призму, боковые ребра которой перпендикулярны к плоскостям оснований. Призмы, боковые ребра которых не перпендикулярны к плоскостям оснований, называют наклонными призмами .
Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.
Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.
Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Видео:ЕГЭ-2021: Объём отсечённой призмы | Задание 8: СтереометрияСкачать

Примеры призм. Треугольные призмы. Четырехугольные призмы.
Параллелепипеды
| Призма | Рисунок | Свойства | |
| Наклонная треугольная призма | 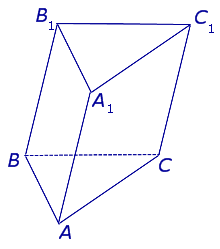 | ||
| Прямая треугольная призма | 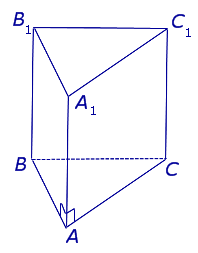 | ||
| Правильная треугольная призма |  | ||
| Наклонная четырехугольная призма | 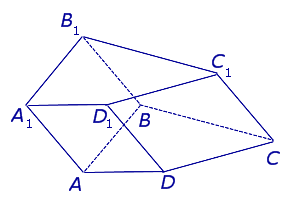 | ||
| Прямая четырехугольная призма | 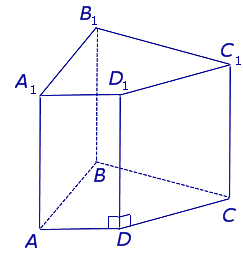 | ||
| Правильная четырехугольная призма | 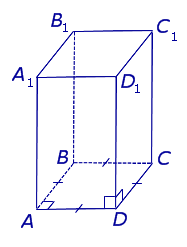 | ||
| Параллелепипед | 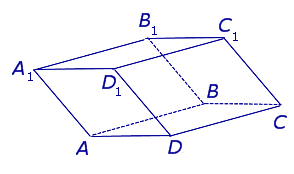 | ||
| Прямой параллелепипед | 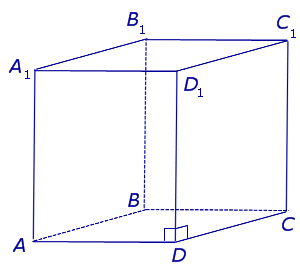 | ||
| Прямоугольный параллелепипед | 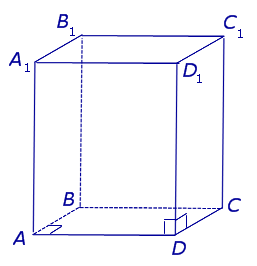 | ||
| Правильный параллелепипед |  | ||
| Куб | 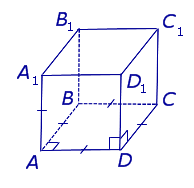 |
| Наклонная треугольная призма |
 |
ABС – произвольный треугольник.


ABСD – произвольный четырехугольник.

Свойства:
Наклонная четырехугольная призма, все грани которой паралллелограммы.
Противоположные грани параллелепипеда равны.
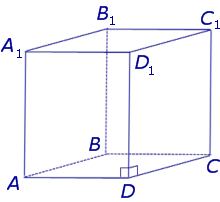
Все грани прямоугольного параллелепипеда являются прямоугольниками.


Свойства:
Правильный параллелепипед, у которого все грани равные квадраты.
У куба все ребра равны и попарно перпендикулярны.
Высота куба равна длине ребра.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Треугольная призма все формулы и примеры задач
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Видео:Через среднюю линию основания треугольной призмы, объем которой , 8 задание ЕГЭ математика профильСкачать

Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Элементы треугольной призмы
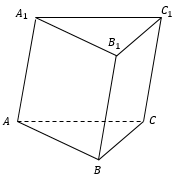
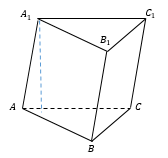
Треугольники ABC и A1B1C1 являются основаниями призмы .
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы .
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Видео:Как строить сеченияСкачать

Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
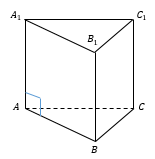
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Видео:Построение сечения параллельно прямойСкачать

Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн . h, то получим:
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы :
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.
Видео:№2. Строим сечения призм — простое свойство!Скачать

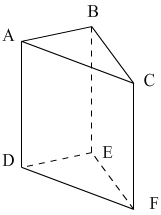
Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Видео:Угол между прямыми Треугольная призмаСкачать

Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k 2 = S12 2 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Видео:10 класс, 30 урок, ПризмаСкачать

Правильная треугольная призма
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Видео:ЕГЭ стереометрия Сечение призмы Площадь сеченияСкачать

Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными треугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности треугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной треугольной призмы:
Правильная треугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной треугольной призмы:
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
🎥 Видео
Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Стереометрия 29 | mathus.ru | расстояние от точки до плоскости в прямой треугольной призмеСкачать

Правильная треугольная призмаСкачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Параллельность прямой к плоскостиСкачать