| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | ||
 | ||
| Большая сторона треугольника | ||
 | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | ||
 | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | ||
 | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | ||
 | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | ||
 | ||
| Углы треугольника | ||
 | ||
| Внешний угол треугольника | ||
 | ||
| Больший угол треугольника | ||
 | ||
| Меньший угол треугольника | ||
 | ||
| Теорема косинусов | ||
 | ||
| Теорема синусов | ||
 | ||
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.


Свойство меньшего угла треугольника:

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

В треугольнике напротив меньшего угла
Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит большая сторона.
2) Если один угол треугольника больше 120°, то два других его угла меньше 30°.
3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
4) Сумма острых углов прямоугольного треугольника не превосходит 90°.
Проверим каждое из утверждений.
1) «В треугольнике против меньшего угла лежит большая сторона.» — неверно, в треугольнике напротив большего угла лежит большая сторона.
2) «Если один угол треугольника больше 120°, то два других его угла меньше 30°.» — неверно, сумма углов в треугольнике равна 180°.
3) «Если все стороны треугольника меньше 1, то и все его высоты меньше 1.» — верно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
4) «Сумма острых углов прямоугольного треугольника не превосходит 90°.» — верно, сумма острых углов треугольника равна 90°.
Видео:Почему напротив большей стороны в треугольнике лежит больший угол?Скачать

Треугольник. Соотношения между углами и сторонами треугольника.
Теорема.
Если любую сторону треугольника продолжить в одном направлении, то образовавшийся при этом внешний угол больше каждого внутреннего угла, не смежного с ним.
Следствие из теоремы.
Если в треугольнике один из углов прямой или тупой, то два других угла будут острые.
Теорема. В любом треугольнике:
1. Напротив равных сторон расположены одинаковые углы.
2. Напротив большей стороны расположен больший угол.
Следствия из теоремы.
2. В разностороннем треугольнике одинаковых углов нет.
Обратные теоремы. В каждом треугольнике:
1. Напротив одинаковых углов расположены одинаковые стороны.
2. Напротив большего угла расположена большая сторона.
Следствия
1. Равноугольный треугольник является и равносторонним.
2. В треугольнике сторона, расположенная напротив тупого или прямого угла, больше других сторон.
💡 Видео
Почему в треугольнике против большей стороны - больший угол ➜ ДоказательствоСкачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

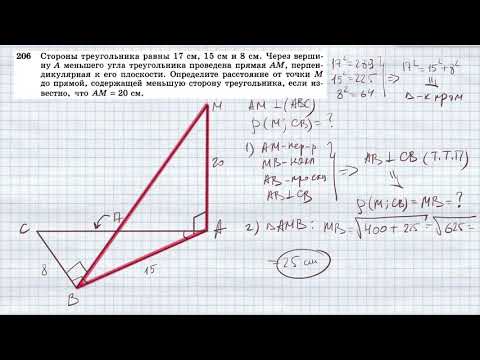
№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать
Против большей стороны треугольника лежит меньший угол. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

В треугольнике против большей стороны лежит ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия | 7 класс| Номер 256 | Атанасян Л.С. | Подробный разборСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Задание 12 ОГЭ вариант 85Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

ОГЭ по математике. Задание 15Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

#24 Самое сложное задание 16 ОГЭ // Вписанный и центральный углы // Теорема синусовСкачать

ОГЭ 2021 Задание 15.Скачать

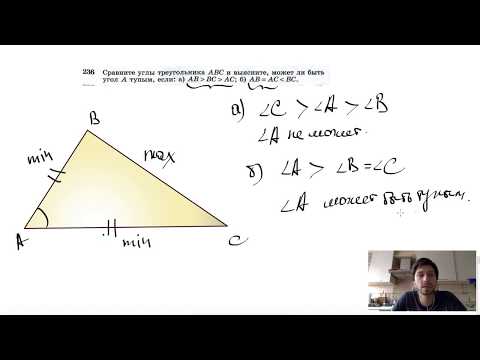
№236. Сравните углы треугольника ABC и выясните, может ли быть угол А тупым, если: а) АВСкачать
Урок 22. Свойство катета прямоугольного треугольника, лежащего против угла в 30° (7 класс)Скачать

Теорема о соотношениях между сторонами и углами треугольника.Скачать

