- Пересечение двух окружностей
- Решение
- Пересечение двух окружностей
- Точки пересечения двух окружностей
- Первая окружность
- Вторая окружность
- Пересечение окружностей
- Координаты пересечения двух окружностей
- Задания по теме «Системы уравнений с параметром»
- Задание №1227
- Условие
- Решение
- Система уравнений с параметром.
- Подробное решение
- Задача для самостоятельного решения.
- 📽️ Видео
Видео:Уравнение окружности (1)Скачать

Пересечение двух окружностей
Даны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают).
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Решение
Предположим, не теряя общности, что центр первой окружности — в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений:
Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных:
Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой:
А решение последней задачи описано в соответствующей статье.
Единственный вырожденный случай, который надо рассмотреть отдельно — когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C — некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ — бесконечность, иначе — точек пересечения нет.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | Окружности не касаются друг друга | r1 + r2″ /> | Одна окружность содержится внутри другой и не касается ее | Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | Окружности соприкасаются в одной точке | Частный случай предыдущего |
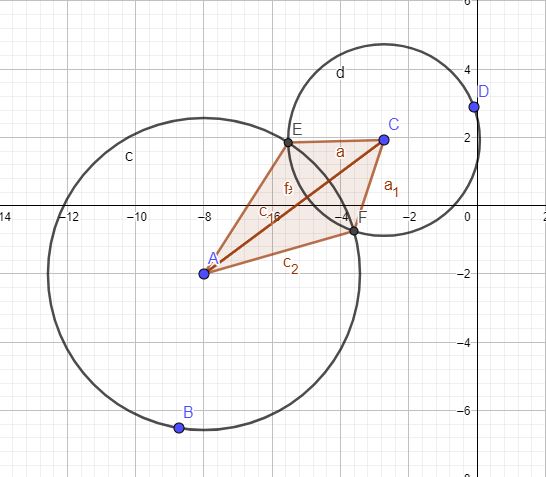
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Координаты пересечения двух окружностей
| Координаты центра первой окружности, через пробел |
| Радиус первой окружности |
| Координаты центра второй окружности, через пробел |
| Радиус второй окружности |
| Координата первого пересечения |
| Координата второго пересечения |
Продолжим изучение геометрии и в этом материале мы рассмотрим, как находить координаты пересечения двух окружностей, если заданы их уравнения. Определение координат двух окружностей на плоскости можно свести к более простым задачам которые мы можем уже решать или понимаем, как их решать. Пусть Две окружности заданы своими двумя уравнениями Повернем изображение на такой угол, что бы линия соединяющая центры окружностей, совпадала с осью абсцисс. Кроме этого перенесем всю схему таким образом, что бы центр одной из окружностей совпал с началом координат.
И алгоритм следующий: 1. Приводим ( линейным смещением) центр первой окружности к координатам (0,0) 3. Определяем угол (W) прямой, проходящей между точками A и C 4. Определяем два угла (psi_1) как сумму и (psi_2) как разность углов W и F 5. Взяв для каждого из углов (в п. 4), синус и умножив на радиус первой окружности мы узнаем координату Y , взяв косинус мы узнаем координату X. 6. Делаем для двух полученных координат, обратное смещение. Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать  Задания по теме «Системы уравнений с параметром»Открытый банк заданий по теме системы уравнений с параметром. Задания C6 из ЕГЭ по математике (профильный уровень) Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать  Задание №1227УсловиеНайдите все значения a > 0, при каждом из которых система begin(x-4)^2+(|y|-4)^2=9,\ x^2+(y-4)^2=a^2end имеет ровно 2 решения. РешениеЕсли y geqslant 0, то первое уравнение задаёт окружность phi _1 с центром в точке C_1 (4; 4) радиуса 3 , а если y то оно задаёт окружность phi _2 с центром в точке C_2 (4; -4) того же радиуса. При a > 0 второе уравнение задаёт окружность phi с центром в точке C(0; 4) радиуса a . Поэтому задача состоит в том, чтобы найти все значения параметра a , при каждом из которых окружность phi имеет ровно две общие точки с объединением окружностей phi _1 и phi _2. Координаты точки касания окружностей phi и phi _1 явно видны на чертеже — точки A_1 (1; 4) и B_1 (7; 4) . То есть при a=CA_1=1 и a=CB_1=7 окружности phi и phi _1 касаются. При a > 7 и a окружности phi и phi _1 не пересекаются, при 1 окружности phi и phi _2 имеют 2 общие точки. Далее, из точки C проведём луч CC_2 и обозначим A_2 и B_2 точки его пересечения с окружностью phi_2 , где A_2 лежит между C и C_2. Заметим, что длина отрезка CC_2= sqrt <4^2+(4-(-4))^>= sqrt = 4sqrt 5. При a или a > CB_2 окружности phi и phi_2 не пересекаются. При CA_2 окружности phi и phi _2 имеют 2 общие точки. При a =CA_2=4sqrt 5-3 или a=CB_2=4sqrt 5+3, окружности phi и phi _2 касаются. Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность phi с одной из окружностей phi _1 и phi _2 имеет 2 общие точки, а с другой не пересекается, либо касается одновременно двух окружностей. Так как 1 то условию задачи удовлетворяют значения ain (1;4sqrt 5-3) cup (7; 4sqrt 5+3). Видео:9 класс, 6 урок, Уравнение окружностиСкачать  Система уравнений с параметром.Задача 1 Найти все значения параметра a, при каждом из которых система уравнений [left< begin ((x+5)^2+y^2-a^2)ln = 0; \ ((x+5)^2+y^2-a^2)(x+y+5-a) = 0 \ endright. ] имеет два различных решения. Условие получено от пользователей сайта alexlarin.net. Задача хорошо решается графическим методом. Мне она показалась интересной тем, что, в отличие от обычной практики, в процессе размышлений здесь графики лучше размещать на отдельных рисунках. Привожу полное решение этой задачи в качестве очередного примера заданий ЕГЭ на параметр. Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать  Подробное решениеРешение любой задачи, содержащей алгебраические выражения, должно начинаться с анализа области допустимых значений (ОДЗ) этих выражений. Особенно важно не забывать об этом при решении заданий второй части ЕГЭ профильного уровня. [ (x+5)^2+y^2-a^2 = 0; \ (x+5)^2+y^2=a^2 ] Получили уравнение окружности на координатной плоскости. Радиус окружности равен абсолютному значению параметра а. В случае, когда а = 0, окружность вырождается в точку. (Не забываем, что r = |а| потому, что нужно рассмотреть все возможные значения параметра, в том числе и отрицательные, которые при возведении в квадрат удовлетворяют уравнению окружности.) Центр окружности расположен в точке с координатами . Изобразим несколько таких окружностей для различных значений параметра а. Анализируем рисунок: Выводы: Итак, продолжаем искать решения заданной системы уравнений среди решений следующей системы, содержащей оставшиеся два сомножителя [left< begin ln = 0; \ (x+y+5-a) = 0. \ endright. ] Последняя равносильна заданной при условии, что нас не интересует случай, когда ((x+5)^2+y^2-a^2 = 0). В дальнейшем эту систему я буду называть сокращенной. Решением сокращенной системы уравнений будут точки пересечения окружности (r = sqrt) с этими прямыми. Прямые могут пересекать окружность в двух точках, касаться её в одной точке или вообще не иметь общих точек с окружностью. Нас интересуют те из них, которые имеют по два пересечения, что будет соответствовать двум различным решениям системы уравнений. Как видно по рисунку, такие прямые находятся между двумя касательными к окружности. Нужно уточнить их уравнения, чтобы найти соответствующие пределы изменения параметра a. Например, для точки применим первый способ: В качестве второго примера, левую точку касания полностью найдём через производную и уравнение касательной. Нижняя часть окружности соответствует графику функции [ y = — sqrt ] Вычислим производную этой функции [ y’ = (- sqrt)’ = -dfrac<2sqrt> = -dfrac<2sqrt> = dfrac<sqrt> ] Приравняем производную к тангенсу угла наклона искомой касательной, т.е. в нашем случае к −1 и решим уравнение относительно x. [dfrac<sqrt> = -1;\ x = — sqrt; ; x^2 = 8-x^2; \ 2x^2 = 8; ; x^2 = 4; ; x = pm2.] Нашли абсциссы точек касания. Подстановкой в уравнение окружности находим ординаты этих точек [ y = — sqrt; ; y(-2) = — sqrt = — sqrt = -2;] Итак, точки касания найдены и обоснованы. Определим соответствующие им значения параметра a. Вернёмся к заданной системе уравнений. Чтобы она имела два различных решения, параметр a должен находиться в таком диапазоне, где первый из рассмотренных нами сомножителей не дает решений (иначе, как мы выяснили, их будет бесконечно много), а система из оставшихся двух сомножителей, сокращенная система, дает ровно два решения. Чтобы определить этот диапазон, найдем пересечение полученных ранее интервалов для параметра а с помощью числовой оси. Как видно оба условия выполняюися для (a in (1; 2]cup [8; 9)) Ответ: (a in (1; 2]cup [8; 9)) Конечно, в итоговое решение, которое будет переписано на бланк, вы можете поместить один рисунок, который выглядит примерно так: В качестве решения приведите все алгебраические выкладки с кратким обоснованием. Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  Задача для самостоятельного решения.Задача 2 Найдите все значения параметра a, при каждом из которых система уравнений [left< begin (x+y-2a)sqrt = 0; \ (x+y-2a) Large (normalsize x^2+(y+3)^2-a^2 Large )normalsize = 0 \ endright. ] имеет ровно два различных решения. 1) ОДЗ: ( 8x-y^2-x^2 ge 0 ) 2) Система равносильна совокупности [ left[ begin x+y-2a = 0; \ <left< begin sqrt = 0; \ x^2+(y+3)^2-a^2 = 0. end right.> end right. ] 3) Первое уравнение совокупности [x+y-2a = 0; \ y=-x+2a ] является уравнением прямых на координатной плоскости. Находим точки касания этих прямых и окружности ОДЗ: [ (x-4)^2+y^2 = 4^2 \ y = pm sqrt \ y’ = pm dfrac<2sqrt> = mp dfrac<sqrt> \ mp dfrac<sqrt> = -1 \ pm (x-4) = sqrt \ (x-4)^2 = 16 — (x-4)^2 \ (x-4)^2 = 8\ x = pm sqrt + 4 = 4 pm 2sqrt. \ y = pm sqrt = pm sqrt = pm 2sqrt. \ ] При каких (a) через точки касания проходят прямые? [ x+y-2a= 0;\ 4+2sqrt+2sqrt = 2a;\ a=2+2sqrt.] [ x+y-2a = 0;\ 4-2sqrt-2sqrt=2a;\ a=2-2sqrt. ] Вывод: 4) Рассматриваем систему совокупности (сокращенную систему): [ <left< begin sqrt = 0; \ x^2+(y+3)^2-a^2 = 0. end right.> ] [sqrt = 0 LeftarrowRightarrow 8x-y^2-x^2=0 LeftarrowRightarrow (x-4)^2+y^2 = 4^2 ] Решениями первого уравнения этой системы являются все точки окружности — границы ОДЗ. Решением системы — пересечение этих множеств. При каких (a) окружности касаются друг друга? Вывод: 5) Общий вывод: Ответ: ( a in (-9;; -1)cup (2+2sqrt;; 9) ) Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ 2018. 📽️ ВидеоМатематика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать  Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать  Решение системы линейных уравнений графическим методом. 7 класс.Скачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Решение систем уравнений второй степени. Алгебра, 9 классСкачать  Уравнение окружностиСкачать  Алгебра 9 класс. Графическое решение систем уравненийСкачать  ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать  Решение систем уравнений второго порядка. 8 класс.Скачать  |







 Теперь мы можем решить данную задачу по несложной формуле.
Теперь мы можем решить данную задачу по несложной формуле.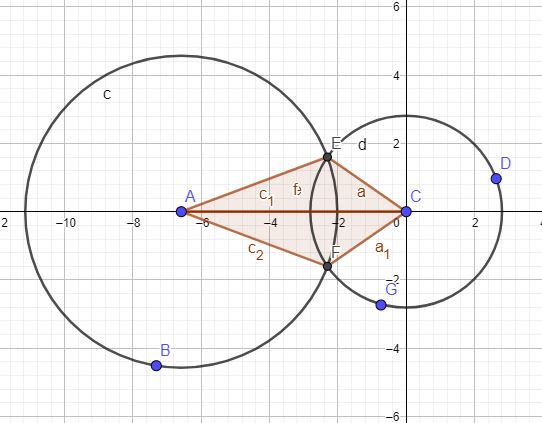


 Здесь одно из уравнений содержит натуральный логарифм, область определения которого ограничена. Следовательно [9-x^2-y^2>0; \ 9>x^2+y^2; \ x^2+y^2 Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Приравняем поочередно каждый сомножитель к нулю, преобразуем к виду, удобному для графического представления и проанализируем его вклад в решение отдельных уравнений и всей системы в целом.
Здесь одно из уравнений содержит натуральный логарифм, область определения которого ограничена. Следовательно [9-x^2-y^2>0; \ 9>x^2+y^2; \ x^2+y^2 Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Приравняем поочередно каждый сомножитель к нулю, преобразуем к виду, удобному для графического представления и проанализируем его вклад в решение отдельных уравнений и всей системы в целом. 
 Преобразуем уравнения, чтобы построить графики [ ln = 0; \ 9-x^2-y^2 = 1; \ 9-1 = x^2+y^2 ; \ x^2+y^2 =8. ] Получили уравнение окружности на координатной плоскости. Радиус окружности равен (sqrt), центр находится в точке . Вся эта окружность находится в области допустимых значений исходной (заданной в условии) системы уравнений. На рисунке она изображена сплошной синей линией. [(x+y+5-a) = 0 \ x+y+5=a ; \ y = -x + (a-5) ] Получили уравнение прямой на координатной плоскости. Прямая проходит параллельно биссектрисе второго и четвертого координатных углов (тангенс угла наклона равен −1) и пересекает ось ординат в точке (a-5). Изобразим несколько таких прямых для различных значений параметра а.
Преобразуем уравнения, чтобы построить графики [ ln = 0; \ 9-x^2-y^2 = 1; \ 9-1 = x^2+y^2 ; \ x^2+y^2 =8. ] Получили уравнение окружности на координатной плоскости. Радиус окружности равен (sqrt), центр находится в точке . Вся эта окружность находится в области допустимых значений исходной (заданной в условии) системы уравнений. На рисунке она изображена сплошной синей линией. [(x+y+5-a) = 0 \ x+y+5=a ; \ y = -x + (a-5) ] Получили уравнение прямой на координатной плоскости. Прямая проходит параллельно биссектрисе второго и четвертого координатных углов (тангенс угла наклона равен −1) и пересекает ось ординат в точке (a-5). Изобразим несколько таких прямых для различных значений параметра а. Если вы очень точно и крупно изобразили координатную плоскость на чертеже, то можно попытаться определить точки касания по рисунку. Например, на увеличенном рисунке с иконкой лупы видно, что касание происходит в точках с координатами и . Однако не забывайте, что экзамен не проверяет ваш глазомер, и истинное значение координаты может отличаться на десятые или сотые доли от видимого, тем более, что радиус окружности у нас имеет иррациональное значение (sqrt). Поэтому, как минимум, необходимы проверка предполагаемых значений координат подстановкой в уравнение окружности и геометрическое обоснование касания. Ещё лучше точно вычислить точки касания через производную и уравнения касательных.
Если вы очень точно и крупно изобразили координатную плоскость на чертеже, то можно попытаться определить точки касания по рисунку. Например, на увеличенном рисунке с иконкой лупы видно, что касание происходит в точках с координатами и . Однако не забывайте, что экзамен не проверяет ваш глазомер, и истинное значение координаты может отличаться на десятые или сотые доли от видимого, тем более, что радиус окружности у нас имеет иррациональное значение (sqrt). Поэтому, как минимум, необходимы проверка предполагаемых значений координат подстановкой в уравнение окружности и геометрическое обоснование касания. Ещё лучше точно вычислить точки касания через производную и уравнения касательных.

 [ 8x-y^2-x^2 = 0 \ 2cdot 4cdot x-y^2-x^2 +16-16=0 \ 16 = x^2 -2cdot xcdot 4+16+y^2 \ (x-4)^2+y^2=4^2 ] ОДЗ — круг радиуса 4 центром в точке О1, включая границу.
[ 8x-y^2-x^2 = 0 \ 2cdot 4cdot x-y^2-x^2 +16-16=0 \ 16 = x^2 -2cdot xcdot 4+16+y^2 \ (x-4)^2+y^2=4^2 ] ОДЗ — круг радиуса 4 центром в точке О1, включая границу.