В треугольнике абс угол б равен 62 прямая мн параллельно ас

Плз напишите доказательство для теоремы как нибудь покороче и простыми словами.

Найти площадь четырехугольника

Геометрия. 8 класс.

Являются ли пирамиды в Египте, тетраэдром??

Как решить задание по геометрии? Теорема косинусов

Составные многогранники. Объём прямоугольного параллелепипеда

Помогите с геометрией

Помогите пожалуйста. Задача по геометрии.

Определение вида треугольника

Математика легко и просто

Найти длины наклонных.

Решите пожалуйста задачи по геометрии Фото ниже

Геометрия 10 класс

Срочно кто поможет геометрия 7класс

Математика, вычисление углов ромба.

Помогите срочно, пожалуйста

Гипотенуза прямоугольного треугольника равна 10, один из острых углов равен 60, найти катеты треугольника

Видео:Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

В треугольнике абс угол б равен 62 прямая мн параллельно ас

АнонимМатематика22 февраля 09:25

Прямая,параллельная стороне AC треугольника ABC,пересекает стороны AB и BC в точках M и H соответственно, MB=2 см , AM=14

см , MH=4 см.Чему равна длина стороны AC?

Ответ или решение1

Это практически типичная задача на подобие треугольников. Так как прямая МН параллельна стороне АС, то по определению МН отсекает от треугольника АВС подобный треугольник МВН. А в подобных треугольниках стороны, находящиеся против равных углов пропорциональны. Или переходя на язык формул, получаем:

АВ : МВ = АС : МН, откуда АС = АВ * МН : МВ.

В данной пропорции для нахождения АС неизвестно значение АВ, которое не трудно найти по её составляющим АМ и МВ.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Применение теорем Менелая и Чевы для решения задач

В пункте 1.5 данной курсовой работы мы рассмотрели теоремы Чевы и Менелая, теперь рассмотри практическое использование данных теорем на примерах.

В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найти отношение Решение:

По условию задачи МА = АС, NC = 3BN. Пусть MA = AC =b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника АВС и продолжение третьей.

По теореме Менелая

Докажите, что медианы треугольника пересекаются в одной точке.

Пусть AM₁, BM₂, СM₃ — медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что

Тогда по теореме Чевы (обратной) отрезки AM₁, BM₂ и СM₃ пересекаются в одной точке.

Итак, доказано, что медианы треугольника пересекаются в одной точке.

На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QL в отношении m:n, считая от точки Q. Найдите

По условию NQ = LR, Пусть NA = LR =a, QF = km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей.

По теореме Менелая

Докажите, что биссектрисы треугольника пересекаются в одной точке.

Тогда по теореме Чевы (обратной) AL₁, BL₂, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника

Перемножая почленно полученные равенства, получаем

Для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке.

В треугольнике АВС AD — медиана, точка O — середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?

Пусть BD = DC = a, AO = OD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника ADC.

По теореме Менелая

Докажите, если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.

Пусть A₁, B₁и C₁ — точки касания вписанной окружности треугольника АВС. Для того чтобы доказать, что отрезки AA₁, BB₁и CC₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C₁B = BA₁ = x, AC₁ = CB₁ = y, BA₁ = AC₁ = z.

Равенство Чевы выполняется, значит, биссектрисы треугольника пересекаются в одной точке.

Рассмотрим два способа решения одной задачи. Первый способ довольно длинный, но данный прием, который в нем используется, применяется довольно часто при решении задач, в которых дано отношение отрезков. Второй способ позволяет решить задачу в одно действие, но в нем используется Теорема Менелая.

Итак задача: На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.

Вот наш треугольник:

Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К:

Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1.

Пусть AC = x, BK = 2x.

Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.

Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC = x, то LB = 1,5x.

Пусть LM = 3n, MC = 2n. Тогда LC = 5n.

Теперь рассмотрим подобные треугольники LOK и AOC.

следовательно, . Пусть LO = 3,5z, OC = z. Тогда LO+OC=LC=4,5z. Получили, что 5n = 4,5z. Тогда MC = 2n = z.

Отсюда MO = MC-CO = z-z = z

Отсюда CO:OM = z:z = 5:4 = 1,25.

Теперь используем при решении данной задачи теорему Минелая. Рассмотрим треугольник MBC и прямую AN:

Запишем теорему Менелая для этого треугольника:

Рассмотрев применение теорем Чевы и Менелая при решении задач можно сделать следующий вывод: знание данных теорем весьма упрощает решение задачи, однако зачастую задачу все таки можно решить и не применяя данных теорем, но, как правило, решение будет весьма объёмным.

💥 Видео

Параллельные прямые | Математика | TutorOnlineСкачать

№63. Параллельные плоскости a и β пересекают сторону АВ угла ВАС соответственно в точках A1 и A2Скачать

№262 В треугольниках ABC и А1В1С1 углы А и А1 — прямые, BD и В1D1— биссектрисы. Докажите, чтоСкачать

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Задание 24 ОГЭ по математике #7Скачать

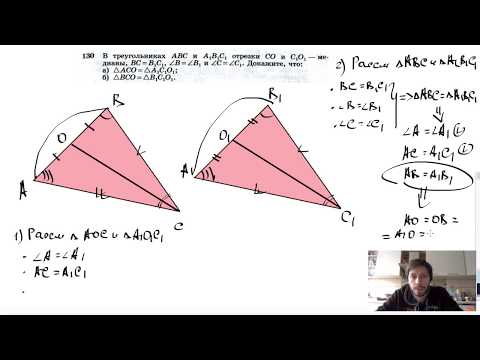
№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать

В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

№230. Биссектрисы углов А и В треугольника ABC пересекаются в точке М. Найдите ∠AMBСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия В треугольнике ABC известно что AB = 12 см BC = 10 см SinA =0,2 Найдите синус угла CСкачать

№542. В подобных треугольниках ABC и KMN стороны АВ и КМ, ВС и MN являются сходственнымиСкачать

№272. В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки DСкачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

ОГЭ Задание 25 Средняя линия прямоугольного треугольникаСкачать

AD= 3/( 4) AC. Найти угол BAC, известно, что BD разбивает треугольник на два подобных треугольникаСкачать