В треугольнике абс через точку м проведены прямые параллельные

Видео:№195. Начертите треугольник ABC и отметьте точку D на стороне АС. Через точку D с помощьюСкачать

Ваш ответ

Видео:№563. Через точку М, взятую на медиане AD треугольника ABC, и вершину В проведена прямая,Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,667
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

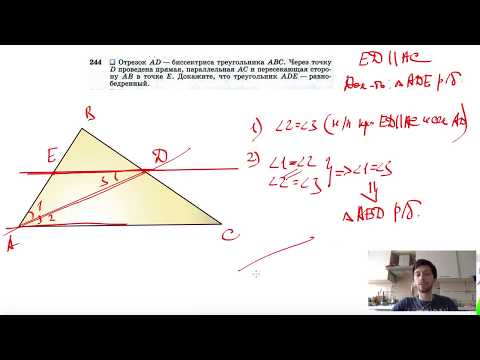
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

1) В треугольнике ABC через точку M, принадлежащую стороне АС, проведена прямая, параллельная стороне АВ, и пересекающая сторону ВС в точке N?

Геометрия | 5 — 9 классы

1) В треугольнике ABC через точку M, принадлежащую стороне АС, проведена прямая, параллельная стороне АВ, и пересекающая сторону ВС в точке N.

A) докажите, что треугольник ABC подобен треугольнику MCN.

B) найдите стороны треугольника ABC, если стороны треугольника MNC равны 4см, 6см, 7см, и точка M делит сторону AC в соотношении 1 : 1 2) В трапеции ABCD (BC||AD) O — точка пересечения диагоналей.

A) докажите, что треугольник COB подобен треугольнику AOD.

B) найдите диагональ BD, если BC = 6 см, AD = 9 см, BO = 4 см.

1) а)треугольники подобны по трем равнымуглам :

а остальные односторонние при параллельных прямых АВ и МН

б) МН получается ср лин

значит все значения треугольника МНС удваиваются

Р = 12 + 8 + 14 = 34

2) а) треугольники подобны и по трем сторонам и по трем углам и даже по двум сторонам и углу между ними

б) диагонали, пересекаясь, делятся так что ДО = ОА, а СО = ОВ,

значит треугольники СОВ и ДОА равнобедренные и подобные(по двум сторонам и углу между ними — вертикальному углу)

Отношение сторон = 6 / 9 = 2 / 3 значит ВО / ОД = 1 / 3, а нам известно что ОВ = 4, значит ОД = (4 / 2) * 3 = 6

ДВ = ДО + ОВ = 6 + 4 = 10

Видео:Геометрия Отрезок AM - биссектриса треугольника ABC. Через точку M проведены прямая, параллельнаяСкачать

Серединный перпендикуляр стороны АС треугольника АВС пересекает его сторону АВ в точке К?

Серединный перпендикуляр стороны АС треугольника АВС пересекает его сторону АВ в точке К.

Найдите сторону АВ треугольника АВС если ВС = 7 см , а периметр треугольника ВКС = 23 см.

Видео:Геометрия Отрезок DM – биссектриса треугольника CDE. Через точку M проведена прямая, параллельнаяСкачать

Докажите , что треугольник АВО подобен треугольнику ДСО , если сторона АВ параллельна стороне СД, отрезки АД и ВС пересекаются в точке О?

Докажите , что треугольник АВО подобен треугольнику ДСО , если сторона АВ параллельна стороне СД, отрезки АД и ВС пересекаются в точке О.

Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Дан треугольник ABC, проведены медианы, точки пересечения медиан со сторонами образуют треугольник A1B1C1, проведены новые медианы треугольника A1B1C1, точки пересечения медиан со сторонами образуют т?

Дан треугольник ABC, проведены медианы, точки пересечения медиан со сторонами образуют треугольник A1B1C1, проведены новые медианы треугольника A1B1C1, точки пересечения медиан со сторонами образуют треугольник A2B2C2.

Доказать — ABC подобен A2B2C2.

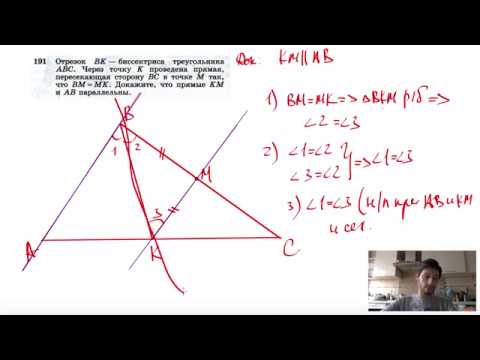
Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

Точка E находится на стороне BC треугольника ABC, BE = 2 см, EC = 3 см?

Точка E находится на стороне BC треугольника ABC, BE = 2 см, EC = 3 см.

Найдите длину стороны BC треугольника ABC.

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

В треугольнике АВС АС = 1 см, АВ = 2 см, О – точка пересечения биссектрис?

В треугольнике АВС АС = 1 см, АВ = 2 см, О – точка пересечения биссектрис.

Отрезок, проходящий через точку О, параллельно стороне ВС, пересекает стороны АС и АВ в точках К и М соответственно.

Найдите периметр треугольника АКМ.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

В треугольнике абс через точку пересечения медиан проведена прямая параллельная стороне ас и пересекающая стороны аб и бс в точка к и е соответственно найдите ас если ке = 12 см найдите площадь треуго?

В треугольнике абс через точку пересечения медиан проведена прямая параллельная стороне ас и пересекающая стороны аб и бс в точка к и е соответственно найдите ас если ке = 12 см найдите площадь треугольника бке если площадь треугольника равна = 72 см.

Видео:№18. Точка C лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и ССкачать

В треугольнике ABC сторона АС поделена на три равных отрезки и через точки деления проведено прямые, паралельные стороне AB треугольника ?

В треугольнике ABC сторона АС поделена на три равных отрезки и через точки деления проведено прямые, паралельные стороне AB треугольника .

Меньший с отрезков этих прямых, что содержат между сторонами треугольника, меньше стороны AB на 8 см.

Найдите сторону АВ треугольника.

Видео:№272. В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки DСкачать

Стороны АD и АВ параллелограмма ABCD равны 15см и 9 см?

Стороны АD и АВ параллелограмма ABCD равны 15см и 9 см.

Найдите периметр треугольника BOC, если периметр треугольника ABC 28 см.

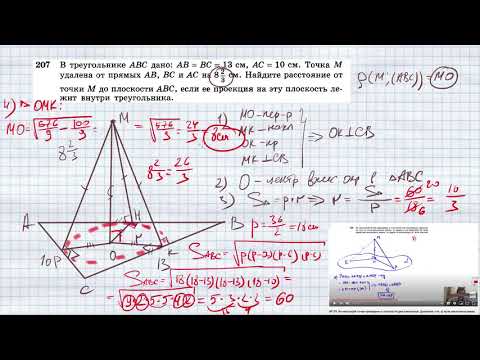
Видео:№207. В треугольнике ABC дано: АВ = ВС = 13 см, AС = 10 см. Точка М удалена от прямых АВ, ВС и АС наСкачать

Помогите СРОЧНО нужно : ) 1) В треугольнике ABC через точку K, принадлежащий стороне AB, проведена прямая, параллельно стороне BC и пересекает сторону AC в точке M?

Помогите СРОЧНО нужно : ) 1) В треугольнике ABC через точку K, принадлежащий стороне AB, проведена прямая, параллельно стороне BC и пересекает сторону AC в точке M.

A) докажите что Δ ABC подобен Δ AKM.

Б) найдите периметр треугольника ABC, если периметр треугольника AKM равен 15 см , а отношение сторон равна AK : AB = 1 : 3.

2) Диагонали AC и BD трапеция ABCD пересекается в точке O.

Через эту точку проведена высота трапеции KM.

Вычислите ее длину, если AO = 7, 5 дм, AM = 6 дм, KC = 2 дм.

3 ) В треугольнике ABCпроведена биссектриса AD, AB = 18 см, BC = 21 см, AC = 24 см.

Найдите BD и DC.

Видео:№212. Прямые, содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В - тупой,Скачать

Медианы треугольника АВС пересекаются в точке О?

Медианы треугольника АВС пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне Ас и пересекающая стороны АВ и ВС в точках К и М соответственно.

Найдите КМ, если сторона АС = 30 см.

Вы перешли к вопросу 1) В треугольнике ABC через точку M, принадлежащую стороне АС, проведена прямая, параллельная стороне АВ, и пересекающая сторону ВС в точке N?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

1) б, т. К. 30 * 2 = 60 2) в, т. К. 120 / 2 = 60 3) б, т. К. 90 — 55 = 35 4) а 5) в, т. К. 180 — 140 = 40.

Вектора перпендикулярны, если их скалярное произведение равно нулю. Запишем скалярное произведение : — 2x + 12 = 0, отсюда x = 6.

1)углы при основании равны т. К. треугольник р / б. (равнобедренный) 2)вершина = 180 — внешний угол = 180 — 130 = 50т. К. они смежные 3)любой угол при основании = (180 — 50) : 2 = 65т. К углы при основании равны и сумма углов треугольника = 180 О..

Вот весь ответ. Надеюсь, помогла.

Ответ 2) в ромб1 из углов равен 90 то квадр.

Сначала проводим касательную к окружности, затем хорду и радиус ОС. Схема и расчет — в приложении.

Ответ : 10 см Объяснение : Дано : АВСМ — трапеция, АВ⊥АМ, ВС = 8 см, ∠ВСМ = 150°. СН — высота. Найти СН. ΔСМН — прямоугольный, ∠МСН = 150 — 90 + 60°, ∠М = 90 — 60 = 30°значит, СН = 1 / 2 СМ как катет, лежащий против угла 30 градусовСН = 20 : 2 = 1..

Самое основное в этой задаче понять, почему треугольник BCD — равнобедренный. Вспомни накрест лежащие углы, они равны при параллельных прямых и секущей третьей. А треугольник является равнобедренным, если его углы при основании равны. Основанием т..

Длина СД = АВ * 5 = 4, 3 * 5 = 21, 5 см АВ + СД = 4, 3 + 21, 5 = 25, 8 см.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В треугольнике абс через точку м проведены прямые параллельные

§ 15. Свойства параллельных прямых

(обратная теореме 14.1)

Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.

На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.3)

Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.

На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.2)

Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .

На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.

Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).

Докажите это следствие самостоятельно.

Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.

Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .

Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .

Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.

Тогда MK = NP .

Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .

Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.

Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .

Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .

Тогда треугольник AMK — равнобедренный.

1. Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
2. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
3. Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
4. Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
5. Что называют расстоянием между двумя параллельными прямыми?

326. На рисунке 230 найдите угол 1.

327. На рисунке 231 найдите угол 2.

328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.

330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:

1) один из этих углов равен 48°;

2) отношение градусных мер двух из этих углов равно 2 : 7.

331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.

332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.

333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.

334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.

335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .

336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .

337. Ответьте на вопросы.

1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?

2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?

3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?

338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .

339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .

340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .

341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .

342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.

343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .

344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .

345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .

346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .

347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .

348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .

349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .

350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.

351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .

352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .

Упражнения для повторения

353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?

354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .

355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?

Наблюдайте, рисуйте, конструируйте, фантазируйте

356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?

🔍 Видео

Геометрия В треугольнике ABC известно, что угол A = 35. Через произвольную точку, принадлежащуюСкачать

Геометрия. ОГЭ по математике. Задание 15Скачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

№121. В треугольнике ABC дано: ∠C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину ССкачать

№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать