Видео:В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

Ваш ответ
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

решение вопроса
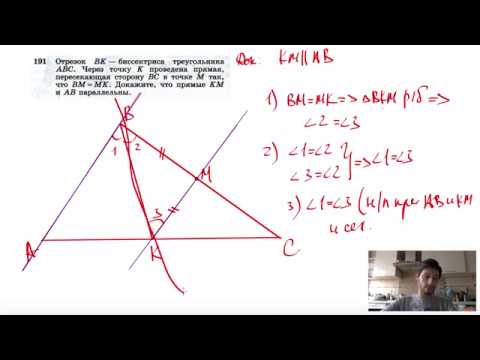
Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать
Похожие вопросы
- Все категории
- экономические 43,283
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,084
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

В треугольнике abc bm биссектриса
В треугольнике ABC проведены биссектрисы BM и CN. Оказалось, что точки B, C, M и N лежат на одной окружности.
а) Докажите, что треугольник ABC равнобедренный.
б) Пусть P — точка пересечения биссектрис треугольника ABC. Найдите площадь четырёхугольника AMPN, если MN : BC = 2 : 5, а BN = 14.
а) Вписанные углы NCM и MBN опираются на одну и ту же дугу, следовательно, они равны. Поскольку
получаем то есть треугольник ABC равнобедренный.
получаем, что и прямая MN параллельна прямой BC. Отрезок BC равен 35.
Пусть AK — биссектриса, медиана и высота треугольника ABC. Прямая AK проходит через точку P — центр вписанной окружности. Треугольник ANM подобен треугольнику ABC, следовательно,
Площадь треугольника ABС равна
В четырёхугольнике AMPN диагонали AP и MN перпендикулярны, следовательно, его площадь равна
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:В треугольнике ABC проведена биссектриса AL ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать  В треугольнике abc bm биссектрисаИз этой теоремы следует, что в треугольнике против равных углов лежат равные стороны . Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный. Рассмотрим треугольник ABC , у которого отрезок BM — медиана и биссектриса. Надо доказать, что AB = BC . На луче BM отложим отрезок MD , равный отрезку BM (рис. 171). В треугольниках AMD и CMB имеем: AM = MC (так как по условию BM — медиана), BM = MD по построению, углы AMD и CMB равны как вертикальные. Следовательно, треугольники AMD и CMB равны по первому признаку равенства треугольников. Тогда стороны AD и BC , углы ADM и CBM равны как соответственные элементы равных треугольников. Так как BD — биссектриса угла ABC , то ∠ ABM = ∠ CBM . Поскольку ∠ CBM = ∠ ADM , то получаем, что ∠ ABM = ∠ ADM . Тогда по теореме 10.3 получаем, что треугольник DAB — равнобедренный, откуда AD = AB . И уже доказано, что AD = BC . Следовательно, AB = BC . Задача. В треугольнике ABC проведена биссектриса BM (рис. 172), ∠ BAK = 70°, ∠ AKC = 110°. Докажите, что BM ⊥ AK . Решение. Так как углы BKA и AKC — смежные, то ∠ BKA = 180° — ∠ AKC . Тогда ∠ BKA = 180° — 110° = 70°. Следовательно, в треугольнике ABK получаем, что ∠ BAK = ∠ BKA = 70°. Треугольник ABK — равнобедренный с основанием AK , и его биссектриса BO ( O — точка пересечения AK и BM ) является также высотой, т. е. BM ⊥ AK .
232. В треугольнике ABC медиана BK перпендикулярна стороне AC . Найдите ∠ ABC , если ∠ ABK = 25°. 233. Серединный перпендикуляр стороны AC треугольника ABC проходит через вершину B . Найдите ∠ C , если ∠ A = 17°. 234. В треугольнике ABC известно, что ∠ ACB = 90°, ∠ A = ∠ B = 45°, CK — высота. Найдите сторону AB , если CK = 7 см. 235. На рисунке 173 ∠ AMK = ∠ ACB , AK = MK . Докажите, что ∆ ABC — равнобедренный. 236. Прямая, перпендикулярная биссектрисе угла A , пересекает его стороны в точках B и C . Докажите, что ∆ ABC — равнобедренный. 237. Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный. 238. В треугольнике ABC биссектриса BK является его высотой. Найдите периметр треугольника ABC , если периметр треугольника ABK равен 16 см и BK = 5 см. 239. Верно ли утверждение: 1) если медиана и высота треугольника, проведённые из одной вершины, не совпадают, то этот треугольник не является равнобедренным; 2) если биссектриса треугольника делит противолежащую сторону пополам, то этот треугольник равнобедренный? 240. Медианы AE и CF , проведённые к боковым сторонам BC и AB равнобедренного треугольника ABC , пересекаются в точке M . Докажите, что треугольник AMC — равнобедренный. 241. Точки M и K принадлежат соответственно боковым сторонам AB и BC равнобедренного треугольника ABC , AM = CK . Отрезки AK и CM пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный. 242. На сторонах AB и BC треугольника ABC отметили соответственно точки D и E так, что ∠ EAC = ∠ DCA . Отрезки AE и CD пересекаются в точке F , DF = EF . Докажите, что ∆ ABC — равнобедренный. 243. Через середину D стороны AB треугольника ABC проведены прямые, перпендикулярные биссектрисам углов ABC и BAC . Эти прямые пересекают стороны AC и BC в точках M и K соответственно. Докажите, что AM = BK . 244. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK . Найдите сторону AB , если BC = 16 см. 245. Прямая, проходящая через вершину A треугольника ABC перпендикулярно его медиане BD , делит эту медиану пополам. Найдите отношение длин сторон AB и AC треугольника ABC . 246. В треугольнике ABC известно, что ∠ C = 90°, ∠ A = 67,5°, ∠ B = 22,5°, CK — биссектриса треугольника ABC , CM — биссектриса треугольника BCK (рис. 174). Докажите, что точка M — середина отрезка AB . 247. Длины сторон треугольника, выраженные в сантиметрах, равны трём идущим подряд натуральным числам. Найдите стороны этого треугольника, если одна из его медиан перпендикулярна одной из его биссектрис. 248. В треугольнике ABC известно, что AB = 3 см, BC = 4 см, AC = 6 см. На стороне BC отметили точку M такую, что CM = 1 см. Прямая, проходящая через точку M перпендикулярно биссектрисе угла ACB , пересекает отрезок AC в точке K , а прямая, проходящая через точку K перпендикулярно биссектрисе угла BAC , пересекает прямую AB в точке D . Найдите длину отрезка BD . Упражнения для повторения 249. На прямой последовательно отметили точки A , B , C , D , E и F так, что AB = BC = CD = DE = EF . Найдите отношения AB : CF , AB : BF , BD : AE . 250. Найдите углы, образованные при пересечении двух прямых, если один из них на 42° больше половины второго угла. Наблюдайте, рисуйте, конструируйте, фантазируйте 251. Разрежьте прямоугольник размером 4 × 9 на две равные части, из которых можно сложить квадрат. 🎥 Видео🔴 В треугольнике ABC проведена биссектриса ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Геометрия В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношенииСкачать  Построение биссектрисы в треугольникеСкачать  Свойство биссектрисы треугольника с доказательствомСкачать  Геометрия В треугольнике ABC известно, что угол A = 44, угол B = 56. Биссектрисы AK и BMСкачать  3 свойства биссектрисы #shortsСкачать  В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать  Геометрия В треугольнике ABC известно, что AC = a, AB = BC = b, AM и CK – биссектрисы треугольникаСкачать  В треугольнике ABC известно, что угол BAC = 42 градуса, AD - биссектриса. Найдите угол BAD. Ответ даСкачать  1704 В треугольнике ABC известно что AC равно 58 BM медиана BM равно 37 Найдите амСкачать  Формула для биссектрисы треугольникаСкачать  Построение биссектрисы угла. 7 класс.Скачать  Построение медианы в треугольникеСкачать  №235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать  ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать  |















