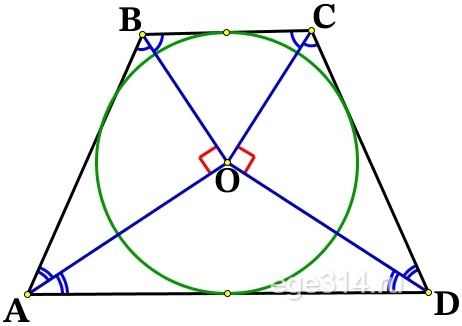
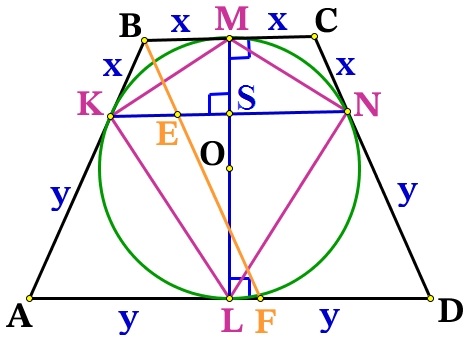
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac площади трапеции ABCD.
Источник: Ященко ЕГЭ 2022 (36 вар)
а)
Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.
∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°
Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:
Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:
∠AOB = ∠COD = 90°
Что и требовалось доказать.
б) Найти: frac , если АВ = СD, S_=fraccdot S_ :
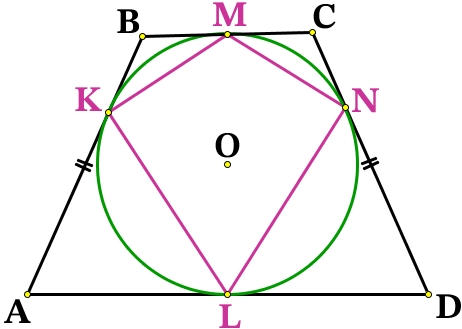
Отрезки касательных к окружности, проведённые из одной точки, равны:
BM = BK
CM = CN
AK = AL
DL = DN
Т.к. AB = CD, то:
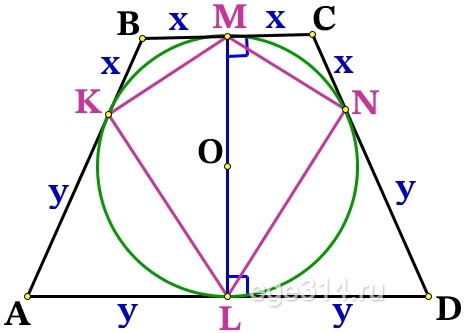
BK = СN = BM = CM = x
AK = DN = AL = DL = y
Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:
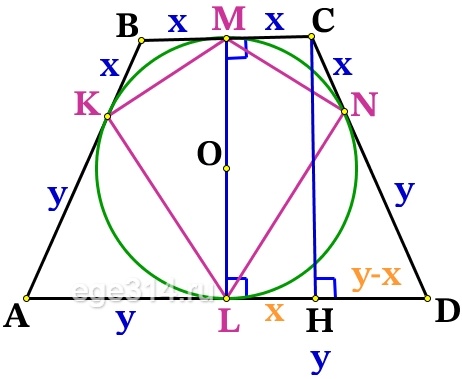
Проведём ещё одну высоту трапеции СН:
MC = LH, МCHL – прямоугольник, значит MC = LH = x , найдём HD:
HD = LD – LH = y – x
Из прямоугольного ΔСHD по теореме Пифагора найдём СН:
СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=sqrt=2sqrt
Выразим площадь SABCD :
В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.
ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:
Найдём диагональ KN:
Выразим площадь SKMNL :
S_=fraccdot MLcdot KNcdot sin angle MSK=fraccdot 2sqrtcdot fraccdot sin 90^=sqrtcdot fraccdot 1= frac<4xysqrt>
Подставим выраженные площади с исходное отношение:
Т.к. у нас у большее основание, а х меньшее, то их отношение равно 6.
Видео:✓ Планиметрия от ЕГЭ до Всероса | #ТрушинLive #032 | Борис ТрушинСкачать

Вариант № 33006762 тренировочный ЕГЭ по математике профильный уровень с ответами
ПОДЕЛИТЬСЯ
Пробный тренировочный вариант №33006762 ЕГЭ по математике 11 класс профильный уровень, 19 тренировочных заданий с решением для проверки.
Ссылка для скачивания варианта (заданий): скачать
Ссылка для скачивания ответов (решений) к варианту: скачать
Решать пробный вариант ЕГЭ 33006762 по математике 11 класс онлайн:
Решения и ответы к варианту 33006762:
Задание 1 №504225) В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?
Ответ: 11
Задание 2 №27512) На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.
Ответ: 20
Задание 3 №502041) На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 34. Найдите площадь закрашенной фигуры.
Ответ: 102
Задание 4 №282856) При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Ответ: 0,006
Задание 5 №26657) Найдите корень уравнения log4(x+3)=log4(4x-15).
Ответ: 6
Задание 6 №27610) Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Ответ: 30
Задание 7 №27505) На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -2
Задание 8 №27102) Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Ответ: 2
Задание 9 №26788) Найдите 3cosa-4sina/2sina-5cosa, если tg a=3.
Ответ:-9
Задание 10 №27962) Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: , где – время в минутах, К, К/мин, К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Ответ:2
Задание 11 №99593) Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Ответ: 45
Задание 12 №26712) Найдите точку минимума функции y=(3-x)e3-x.
Ответ: 4
Задание 13 №514623) а) Решите уравнение 6log 2/8x-5log8x+1=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [2;2,5].
Задание 14 №520190) Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60 градусов. а) Докажите, что ABCD — квадрат. б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен корень из 2
Ответ: 0,8
Задание 15 №508213) Решите неравенство: 1/x-1+1/2-x
Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Задача 8190 В равнобедренную трапецию ABCD с.
Условие
В равнобедренную трапецию ABCD с основаниями AD и BC вписана окружность, CH — высота трапеции.
а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке BH.
б) Найдите диагональ AC, если известно, что средняя линия трапеции равна 2sqrt(7), а угол AOD=120 градусов, где O — центр окружности, вписанной в трапецию, а AD — большее основание.
Решение
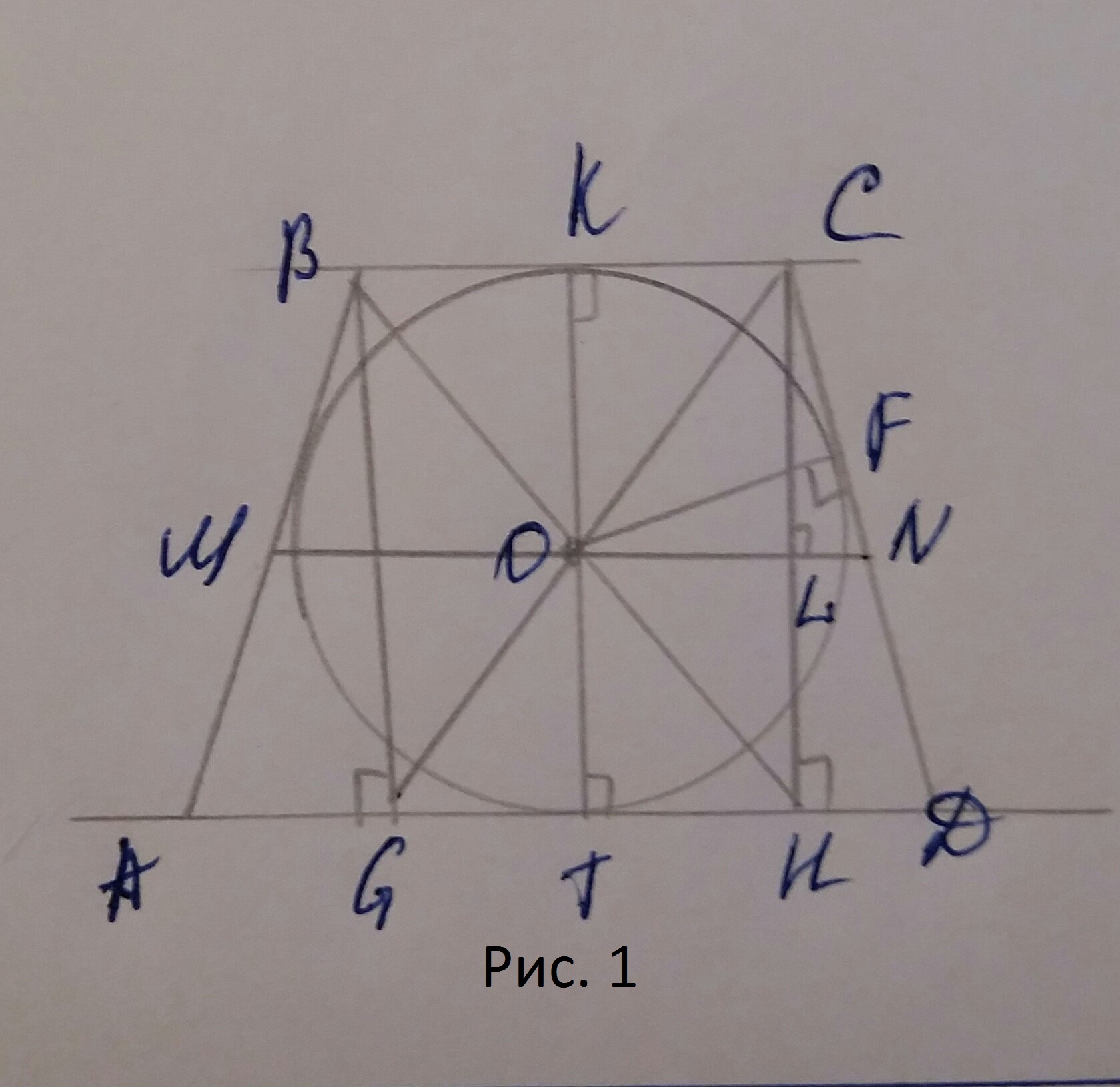
а)См. рис. 1
BG⊥AD; GBCH-прямоугольник
Пусть О=BH⋂CG
Докажем, что О-центр вписанной окружности.
KT⊥BC; OK=OT, т.е. О равноудалена от ВС и AD.
MN-средняя линия трапеции,
MN=CD по свойству описанной равнобедренной трапеции.
Тогда, ON=CN
⇒ △ONC-равнобедренный,
OF и CL его высоты, проведенные к равным сторонам,
⇒ OF=CL=KO, т.е. О равноудалена от BC,CD, AD(аналогично и от AB).
Значит, О-центр вписанной окружности и О∈ВН.
б)См. рис. 2
По свойству описанной равнобедренной трапеции CD=MN=2sqrt(7)
Из △AOD: ∠ADO=(180°-120°):2=30°.
∠ODC=∠ADO=30°(OD-биссектриса).
Из △CHD: ∠DCH=90°-60°=30°, ⇒HD=1/2*CD=1/2*2sqrt(7)=sqrt(7), по теореме Пифагора: CH=sqrt((2sqrt(7))^2-(sqrt(7))^2)=sqrt(28-7)=sqrt(21).
Так как трапеция описано около окружности AD+ВС=AB+CD=2sqrt(7)+2sqrt(7)=4sqrt(7)
AD=2HD+BC
Тогда, 2HD+BC+BC=4sqrt(7)
2BC=4sqrt(7)-2sqrt(7)
2BC=2sqrt(7)
BC=sqrt(7)
⇒ AH=sqrt(7)+sqrt(7)=2sqrt(7).
По теореме Пифагора из △АСН: АС=sqrt((sqrt(21))^2+(2sqrt(7))^2)=sqrt(21+28)=sqrt(49)=7 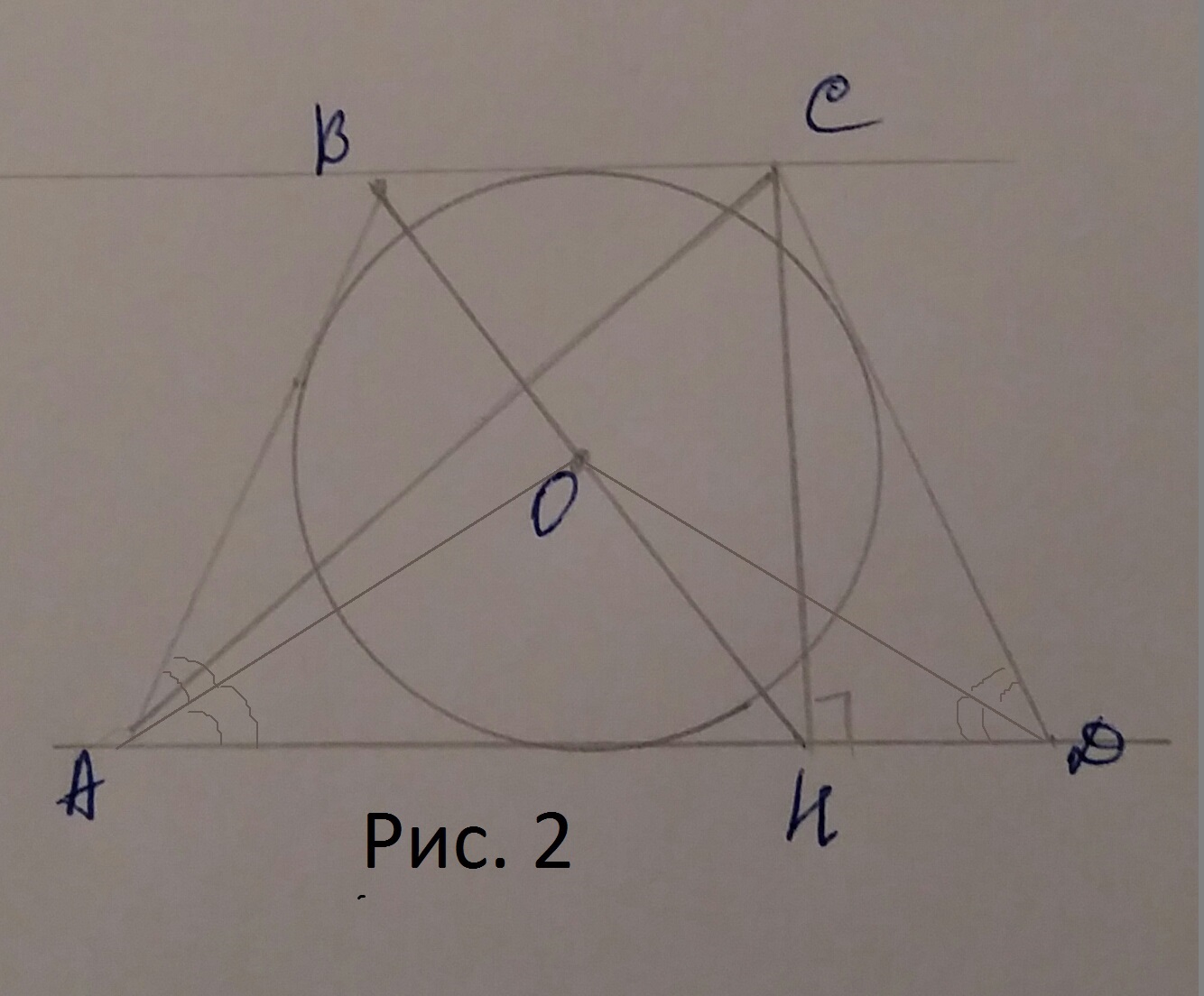
📽️ Видео
4.43.1. Планиметрия. Гордин Р.К.Скачать

ЕГЭ математика 2022 задача 16 вариант 3Скачать

Где центр окружности? ТрапецияСкачать

№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Школково - ЕГЭ по математике. Планиметрия. Сезон 1. Серия 3. Трапеция. Окружность. Синус. 16 задачаСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

8 класс, 6 урок, ТрапецияСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

8 класс, 15 урок, Площадь трапецииСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

ЕГЭ математика 2023 вариант 3 задача 16 ПланиметрияСкачать
Параллельные прямые | Математика | TutorOnlineСкачать

Радиус описанной окружности трапецииСкачать

№30. Основание АВ трапеции ABCD параллельно плоскости α, а вершина С лежитСкачать

✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать

Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать