Как определить выпуклый треугольник

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Определение

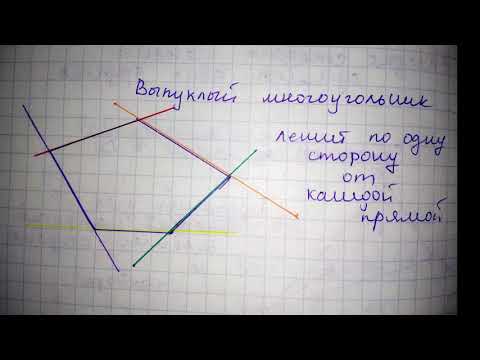
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.

Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.

Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.

В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Выпуклый многоугольник

Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?

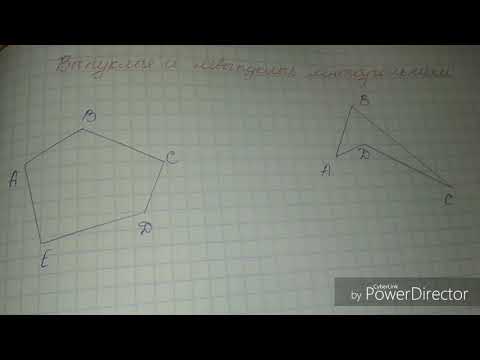
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.

То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.

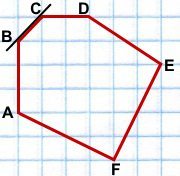
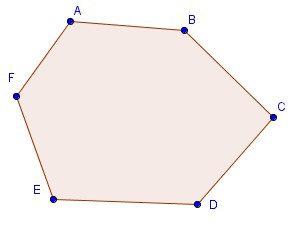
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.

2) MNKFEL — не выпуклый шестиугольник,

Он не лежит в одной полуплоскости относительно прямых KF и FE.

Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.

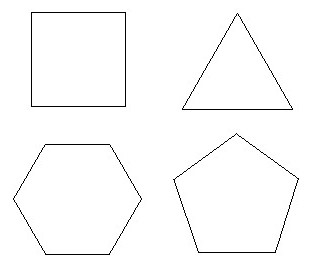
Важнейшие виды выпуклых многоугольников

• Треугольники (в частности, прямоугольные, равнобедренные, равносторонние (правильные))
• Параллелограммы (в частности, прямоугольники, ромбы, квадраты)
• Трапеции (в частности, прямоугольные и равнобедренные)
• Правильные многоугольники.

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Выпуклые многоугольники. Определение выпуклого многоугольника. Диагонали выпуклого многоугольника

Данные геометрические фигуры окружают нас повсюду. Выпуклые многоугольники бывают природными, например, пчелиные соты или искусственными (созданными человеком). Эти фигуры используются в производстве различных видов покрытий, в живописи, архитектуре, украшениях и т.д. Выпуклые многоугольники обладают тем свойством, что все их точки располагаются по одну сторону от прямой, что проходит через пару соседних вершин этой геометрической фигуры. Существуют и другие определения. Выпуклым называется тот многоугольник, который расположен в единой полуплоскости относительно любой прямой, содержащей одну из его сторон.

Видео:№365. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равенСкачать

Выпуклые многоугольники

Вершины многоугольника называют соседними, в том случае если они представляют собой концы одной из его сторон. Геометрическая фигура, у которой имеется n-е число вершин, а значит, и n-е количество сторон, называется n-угольником. Саму ломаную линию называют границей или контуром этой геометрической фигуры. Многоугольной плоскостью или плоским многоугольником называют конечную часть любой плоскости, им ограниченной. Соседними сторонами этой геометрической фигуры называют отрезки ломаной линии, исходящие из одной вершины. Они будут не соседними, если исходят их разных вершин многоугольника.

Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Другие определения выпуклых многоугольников

• каждый отрезок, что соединяет две любые точки внутри него, полностью лежит в нем;

• внутри него лежат все его диагонали;

• любой внутренний угол не превышает 180°.

Многоугольник всегда разбивает плоскость на 2 части. Одна из них – ограниченная (она может быть заключена в круг), а другая — неограниченная. Первую называют внутренней областью, а вторую – внешней областью этой геометрической фигуры. Данный многоугольник является пересечением (иными словами — общей составляющей) нескольких полуплоскостей. При этом каждый отрезок, имеющий концы в точках, которые принадлежат многоугольнику, полностью принадлежит ему.

Видео:Выпуклый многоугольник | Геометрия 7-9 класс #40 | ИнфоурокСкачать

Разновидности выпуклых многоугольников

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Правильные выпуклые многоугольники

Правильный четырехугольник – квадрат. Правильный треугольник называют равносторонним. Для таких фигур существует следующее правило: каждый угол выпуклого многоугольника равен 180° * (n-2)/ n,

где n – число вершин этой выпуклой геометрической фигуры.

Площадь любого правильного многоугольника определяют по формуле:

где p равно половине суммы всех сторон данного многоугольника, а h равно длине апофемы.

Видео:Выпуклые и невыпуклые многоугольникиСкачать

Свойства выпуклых многоугольников

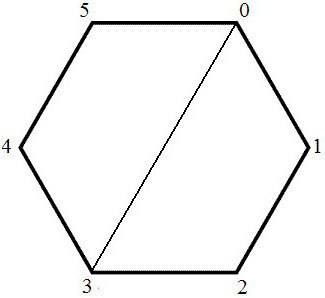
Предположим, что Р – данный выпуклый многоугольник. Берем 2 произвольные точки, например, А, В , которые принадлежат Р. По существующему определению выпуклого многоугольника эти точки расположены в одной стороне от прямой, что содержит любую сторону Р. Следовательно, АВ также имеет это свойство и содержится в Р. Выпуклый многоугольник всегда возможно разбить на несколько треугольников абсолютно всеми диагоналями, которые проведены из одной его вершины.

Видео:Вариант 41, № 6. Как определить кол-во сторон правильного многоугольника, если известен его угол?Скачать

Углы выпуклых геометрических фигур

Углы выпуклого многоугольника – это углы, что образованы его сторонами. Внутренние углы находятся во внутренней области данной геометрической фигуры. Угол, что образован его сторонами, которые сходятся в одной вершине, называют углом выпуклого многоугольника. Углы, смежные с внутренними углами данной геометрической фигуры, называют внешними. Каждый угол выпуклого многоугольника, расположенный внутри него, равен:

где х – величина внешнего угла. Эта простая формула действует в отношении любых геометрических фигур такого типа.

В общем случае, для внешних углов существует следующие правило: каждый угол выпуклого многоугольника равен разности между 180° и величиной внутреннего угла. Он может иметь значения в пределах от -180° до 180°. Следовательно, когда внутренний угол составляет 120°, внешний будет иметь величину в 60°.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Сумма углов выпуклых многоугольников

где n – число вершин n-угольника.

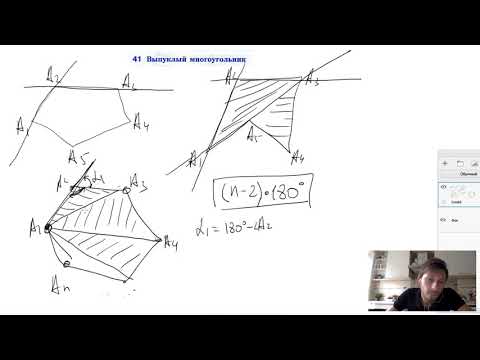
Сумма углов выпуклого многоугольника вычисляется довольно просто. Рассмотрим любую такую геометрическую фигуру. Для определения суммы углов внутри выпуклого многоугольника необходимо соединить одну из его вершин с другими вершинами. В результате такого действия получается (n-2) треугольника. Известно, что сумма углов любых треугольников всегда равна 180°. Поскольку их количество в любом многоугольнике равняется (n-2), сумма внутренних углов такой фигуры равняется 180° х (n-2).

Сумма углов выпуклого многоугольника, а именно любых двух внутренних и смежных с ними внешних углов, у данной выпуклой геометрической фигуры всегда будет равна 180°. Исходя из этого, можно определить сумму всех ее углов:

Сумма внутренних углов составляет 180° * (n-2). Исходя из этого, сумму всех внешних углов данной фигуры устанавливают по формуле:

180° * n-180°-(n-2)= 360°.

Сумма внешних углов любого выпуклого многоугольника всегда будет равна 360° (независимо от количества его сторон).

Внешний угол выпуклого многоугольника в общем случае представляется разностью между 180° и величиной внутреннего угла.

Видео:Геометрия. 8 класс. Выпуклый многоугольник /10.09.2020/Скачать

Другие свойства выпуклого многоугольника

Помимо основных свойств данных геометрических фигур, у них есть и другие, которые возникают при манипуляциях с ними. Так, любой из многоугольников может быть разделен на несколько выпуклых n-угольников. Для этого необходимо продолжить каждую из его сторон и разрезать эту геометрическую фигуру вдоль этих прямых линий. Разбить любой многоугольник на несколько выпуклых частей можно и таким образом, чтобы вершины каждого из кусков совпадали со всеми его вершинами. Из такой геометрической фигуры можно очень просто сделать треугольники путем проведения всех диагоналей из одной вершины. Таким образом, любой многоугольник, в конечном счете, можно разбить на определенное количество треугольников, что оказывается весьма полезным при решении различных задач, связанных с такими геометрическими фигурами.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Периметр выпуклого многоугольника

Отрезки ломаной линии, называемые сторонами многоугольника, чаще всего обозначаются следующими буквами: ab, bc, cd, de, ea. Это стороны геометрической фигуры с вершинами a, b, c, d, e. Сумма длины всех сторон этого выпуклого многоугольника называют его периметром.

Видео:№364. Найдите сумму углов выпуклого: а) пятиугольника; б) шестиугольника; в) десятиугольника.Скачать

Окружность многоугольника

Выпуклые многоугольники могут быть вписанными и описанными. Окружность, касающаяся всех сторон этой геометрической фигуры, называется вписанной в нее. Такой многоугольник называют описанным. Центр окружности, которая вписана в многоугольник, представляет собой точку пересечения биссектрис всех углов внутри данной геометрической фигуры. Площадь такого многоугольника равняется:

где r – радиус вписанной окружности, а p – полупериметр данного многоугольника.

Окружность, содержащую вершины многоугольника, называют описанной около него. При этом данная выпуклая геометрическая фигура называется вписанной. Центр окружности, которая описана около такого многоугольника, представляет собой точку пересечения так называемых серединных перпендикуляров всех сторон.

Видео:Многоугольники. 8 класс.Скачать

Диагонали выпуклых геометрических фигур

Число диагоналей выпуклого многоугольника играет важную роль в элементарной геометрии. Число треугольников (К), на которые возможно разбить каждый выпуклый многоугольник, вычисляется по следующей формуле:

Количество диагоналей выпуклого многоугольника всегда зависит от числа его вершин.

Видео:41. Выпуклый многоугольникСкачать

Разбиение выпуклого многоугольника

В некоторых случаях для решения геометрических задач необходимо разбить выпуклый многоугольник на несколько треугольников с непересекающимися диагоналями. Эту проблему можно решить путем выведения определенной формулы.

Определение задачи: назовем правильным некое разбиение выпуклого n-угольника на несколько треугольников диагоналями, пересекающимися только в вершинах этой геометрической фигуры.

Решение: Предположим, что Р1, Р2 , Р3 … , Pn – вершины этого n-угольника. Число Xn — количество его разбиений. Внимательно рассмотрим полученную диагональ геометрической фигуры Pi Pn. В любом из правильных разбиений Р1 Pn принадлежит определенному треугольнику Р1 Pi Pn, у которого 1 17 апреля, 2014

💥 Видео

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Выпуклый четырехугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

363 ГДЗ по геометрии 8 класс Атанасян - выпуклый многоугольникСкачать