В скольких точках пересекаются 18 прямых среди которых нет параллельных ровно 3 пересекаются

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:№3. Проведите три прямые так, чтобы каждые две из них пересекались.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Комбинаторная задача о числе точек пересечения прямых

Известная комбинаторная задача 1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006. 2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка «Первого сентября». Математика. Вып. 5 (11)). – М.: Чистые пруды, 2006.

Задача о количестве точек пересечения n прямых На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых. Пример. n=5, 10 точек пересечения

Цели работы 1) обобщить одну из известных комбинаторных задач по геометрии и получить полное решение новых задач; 2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.

Задача 1. Наличие параллельных прямых На плоскости провели n прямых, среди которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=8, k=3 25 точек пересечения Пример 2. n=8, k=4 22 точки пересечения

О методе рекуррентных соотношений Метод сведения комбинаторной задачи к аналогичной задаче для меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений. Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д. Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.

Решение задачи №1 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

Нахождение числа точек пересечения

Таблица и рекуррентные соотношения k m Параллельные прямые 2 3 4 5 Прямые общего положения 1 2 3 4 5 2 5 7 9 11 3 9 12 15 18 4 14 18 22 26 5 20 25 30 35

Задача 2. Наличие пар параллельных прямых На плоскости провели n прямых, среди которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=5, k=2 19 точек пересечения Пример 2. n=6, k=3 33 точки пересечения

Решение задачи №2 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

Нахождение числа точек пересечения

Таблица и рекуррентные соотношения k m Пары параллельных прямых 2 3 4 5 Прямые общего положения 1 2 8 18 32 2 5 13 25 41 3 9 19 33 51 4 14 26 42 62 5 20 34 52 74

СПАСИБО ЗА ВНИМАНИЕ!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Именно учебная деятельность как универсальный способ учения определяет особую деятельностную образовательную технологию: переход от «ситуации успеха» к «ситуации разрыва» через рефлексивную оценку (постановку учебной задачи); моделирование и конструирование (этап решения учебной задачи); продвижение от диагностической работы на «входе» через коррекцию к диагностической работе на «выходе» (этап решения частных задач); проверочная работа как переход от одной учебной задачи к другой (констатирующая оценка); перенос способов действий и средств в квазиреальные ситуации (этап решения проектных задач).

Основной принцип построения деятельностной технологии — цикличность (ритмичность) разворачивания образовательного процесса, в котором выделяются три цикла: пятилетний, годовой и тематический.

В рамках реализации деятельностной технологии необходимо особое внимание уделять контрольно-оценочной деятельности. Целесообразно развести контроль и оценку как учебные действия младших школьников и контроль и оценку как педагогические действия.

При деятельностной технологии педагогом создаются разные образовательные пространства:

Видео:ВСЕ ТИПЫ НОМЕРА 22 ИЗ ФИПИ. ОГЭ по Математике 2023. Занятие 5. Февраль. Онлайн школа EXAMhackСкачать

в скольких точках пересекаются 18 прямых среди которых нет параллельных, ровно 3 пересекаются в одной точке, а никакие три другие прямые не проходят через одну точку?

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Ответы на вопрос

существует теорема: вписанный угол равен половине дуги на которую он опирается

значит, если дуга равна 140 градусов, то угол равен 70 градусов

ответ: угол равен 70 градусов

1 — бесчисленное множество плоскостей

2 — одну плоскость

3 — одну или бесчисленное множество плоскостей

площадь основания = 1*2=2

площадь поверхности равна = 2sосн +s=16

диагональ основания равна l=√(2^2+1^2)=√5

диагональ параллелепипеда d=√(l^2+h^2)=√(5+4)=3

пусть сторона второго квадрата равна x, тогда первого (x+10) тогда

Видео:ПЕРЕСЕЧЕНИЕ прямых | ТОЧКА пересечения | Линейные функцииСкачать

в скольких точках пересекаются 18 прямых среди которых нет параллельных, ровно 3 пересекаются в одной точке, а никакие три другие прямые не проходят через одну точку?

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Ответы на вопрос

существует теорема: вписанный угол равен половине дуги на которую он опирается

значит, если дуга равна 140 градусов, то угол равен 70 градусов

ответ: угол равен 70 градусов

1 — бесчисленное множество плоскостей

2 — одну плоскость

3 — одну или бесчисленное множество плоскостей

площадь основания = 1*2=2

площадь поверхности равна = 2sосн +s=16

диагональ основания равна l=√(2^2+1^2)=√5

диагональ параллелепипеда d=√(l^2+h^2)=√(5+4)=3

пусть сторона второго квадрата равна x, тогда первого (x+10) тогда

🌟 Видео

✓ Три способа решить задачу с параметром | ЕГЭ-2017. Задание 18. Математика. Профиль | Борис ТрушинСкачать

6 класс, 23 урок, Пересечение прямыхСкачать

Пересечения прямых, лучей, отрезковСкачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Координатная прямая. Противоположные числа. 6 класс.Скачать

Профильный ЕГЭ 2023. Математика. Задачи 1-11 первая частьСкачать

№ 601-700 - Алгебра 8 класс ДорофеевСкачать

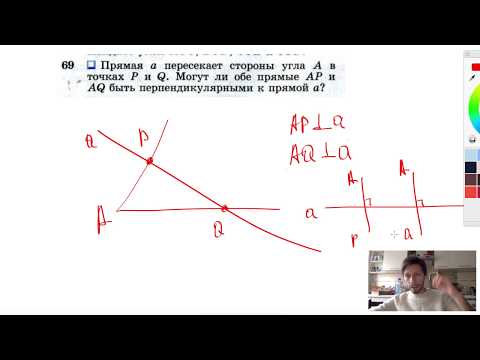
№69. Прямая а пересекает стороны угла А в точках Р и Q. Могут ли обе прямые АР и AQСкачать

5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Все Задания 8 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать