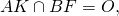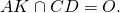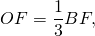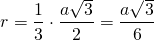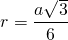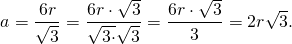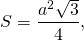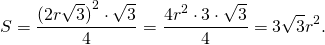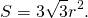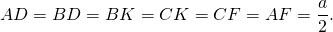Видео:Точка O центр окружности описанной около остроугольного треугольникаСкачать

Ваш ответ
Видео:ОГЭ без рекламы математика 17 вариант задача 25Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равностороннем треугольнике abc точка o центр вписанной окружности
Сторона AB треугольника ABC c тупым углом C равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
По теореме синусов:
Поскольку угол C тупой, а его синус равен это угол 150°.
Приведём другое решение.
Пусть точка О — центр окружности, тогда ОА и ОВ — ее радиусы. Треугольник АОВ равносторонний, поэтому угол АОВ равен 60°. Центральный угол измеряется дугой, на которую он опирается, поэтому дуга АСВ равна 60°. Следовательно, вписанный угол АСВ опирается на дугу 360° − 60° = 300°. Тем самым угол АСВ равен 150°.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Окружность, вписанная в правильный треугольник
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.

точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:
💡 Видео
✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Геометрия В треугольнике ABC точка O – центр описанной окружности, точка L – середина стороны ABСкачать

Геометрия На дуге AC окружности, описанной около равностороннего треугольника ABC, отмечена точка MСкачать

Вписанная окружность в равностороннем треугольникеСкачать

Задание 16 ЕГЭ по математикеСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вариант 30, № 6. Нахождение периметра равностороннего треугольника, в который вписана окружностьСкачать

15 задание треугольники огэ по математике / маттаймСкачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Равносторонний треугольникСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать