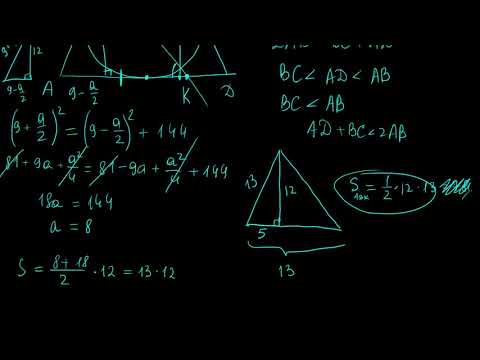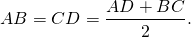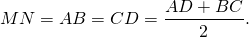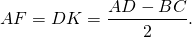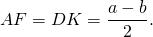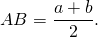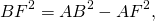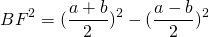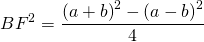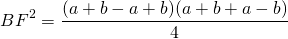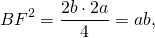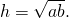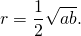В равнобочную трапецию вписана окружность радиуса r верхнее основание

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

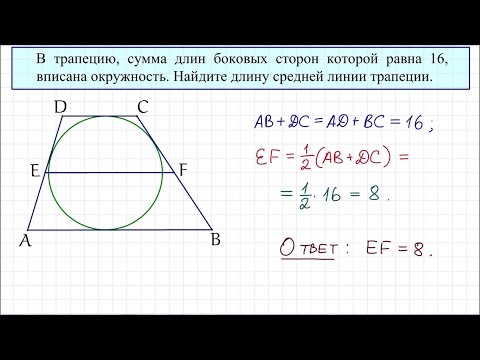
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

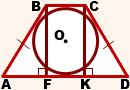
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Видео:Геометрия В равнобедренную трапецию, меньшее основание которой равно 4 см, вписана окружностьСкачать

В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r?

Геометрия | 5 — 9 классы

В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r.

Докажите, что S = 2cr.

Равнобедренная трапеция : боковые стороны с, нижнее основание а и верхнее основание b, высота трапеции h.

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон : 2с = а + b.

Такжевысота трапеции совпадает с диаметром вписанной окружности, значит h = 2r.

S = (a + b) * h / 2 = 2c * 2r / 2 = 2cr.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2?

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2.

Найдите боковую сторону трапеции.

Видео:Геометрия В равнобедренную трапецию вписана окружность радиуса R. Верхнее основание трапеции в 2Скачать

В равнобедренную трапецию вписана окружность?

В равнобедренную трапецию вписана окружность.

Точка касания окружности с боковой стороной делит эту сторону на отрезки с длинами 16 и 25.

Найти площадь трапеции.

Видео:Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапецииСкачать

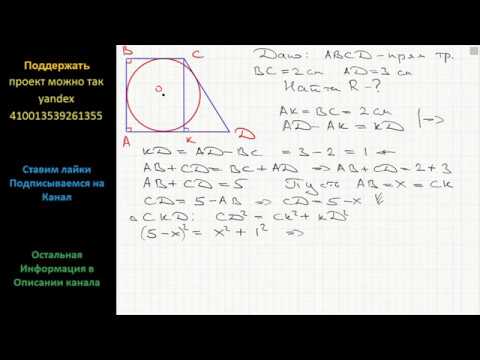
Дана равнобедренная трапеция, её площадь равна 125?

Дана равнобедренная трапеция, её площадь равна 125.

В трапецию вписана окружность так, что расстояние между точками касания её боковых сторон равно 8.

Найдите радиус окружности, вписанной в трапецию.

Видео:Задание 24 ОГЭ по математике #4Скачать

Окружность радиуса 12 вписана в равнобедренную трапецию?

Окружность радиуса 12 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Найдите периметр трапеции.

Видео:Геометрия В прямоугольную трапецию вписана окружность радиуса 12 см Большая из боковых сторон точкойСкачать

Радиус вписанного в равнобедренную трапецию окружности равняется 12см?

Радиус вписанного в равнобедренную трапецию окружности равняется 12см.

Боковая сторона 25см.

Найти основания трапеции.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Окружность радиуса 12 вписана в равнобедренную трапецию?

Окружность радиуса 12 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Найдите периметр трапеции.

Видео:Задача про трапецию, описанную около окружностиСкачать

В равнобедренную трапецию вписана окружность радиуса 2?

В равнобедренную трапецию вписана окружность радиуса 2.

Найдите площадь трапеции если длинна боковой стороны равна 10.

Видео:Геометрия Около окружности радиуса √2 описана равнобедренная трапеция, у которой одно основаниеСкачать

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м?

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м.

Найдите площадь трапеции.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

В равнобедренную трапецию с основаниями 8 и 2 вписана окружность?

В равнобедренную трапецию с основаниями 8 и 2 вписана окружность.

Найдите радиус окружности касающейся большего основания боковой стороне и вписанной окружности.

Видео:Окружность вписана в равнобедренную трапецию. Теорема в задаче. Геометрия, ОГЭ, ЕГЭ. Высота и радиусСкачать

В равнобедренную трапецию ABCD с основаниями BC = 9см AD = 25см вписана окружность с центром О а) найдите длину боковой стороны трапеции б) найдите радиус вписанной окружности в) докажите что треуголь?

В равнобедренную трапецию ABCD с основаниями BC = 9см AD = 25см вписана окружность с центром О а) найдите длину боковой стороны трапеции б) найдите радиус вписанной окружности в) докажите что треугольник АОВ прямоугольный.

На этой странице находится ответ на вопрос В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Т. к. Сумма двух углов 90град. То получаем ур — е : x + x + 44 = 90 2x = 46 x = 23.

ABCD — параллелограмм ( я так поняла, что это параллелограмм), AC и BD — диагонали параллелограмма, значит АО = ОС, ВО = ОD (т. К. диагонали параллелограмма точкой пересечения делятся пополам), угол АОВ = угол СОD (как вертикальные), следовательно т..

1) 180 — 40 = 140 так полeче угол AOB 2)ADC — равнобедренный так как AD = DC значит 180 — 80 = 100 это сума углов OAD и DCO так как они ровны разделим 100 : 2 = 50 угол DCO = 50, ответ : УГОЛ DOC = 90 угол DCO = 50 угол СDO = 40 3) не знаю но может в..

План анализа стихотворения А. С. Пушкина «Анчар» 1. История создания произведения 2. Композиция (построение художественного произведения) 3. Тема, главная мысль и идея стихотворения 4. Характеристика лирического героя 5. Приемы раскрытия образо..

В₁А = а , В₁С₁ = в , В₁В = с В₁М = В₁В + В₁Д = с + (В₁В + ВД) = с + с + (ВС + СД) = 2с + (В₁С₁ + В₁А) = 2с + в + а.

Докажите через равенство треугольников по двум сторонкам и углу между ними(как соответственные элементы). Для этого запишите что АО = ОВ и МО = ОН, так как это диаметры. Потом запишите, что углы АОМ и НОВ равны, как вертикальные, а значит треугольн..

Ответ : 128°, 52°Объяснение : Дано : ABCD — прямоугольник, AB и CD — диагонали, ∠ABD = 64°. Найти ∠COD и AOD. Диагонали прямоугольника равны и в точке пересечения делятся пополам. Рассмотрим ΔABD — прямоугольный. Сумма острых углов прямоугольного..

Т. к. Треугл р / б то углы при основании равны(по 40°) значит тупой угол = 180 — (40 + 40) = 100°.

Проведем высоты из вершин В и С Средняя линия = (АD + BC) / 2 = (AE + EF + FD + BC) / 2 Т. К. трапеция равнобедренная, то FD = AE BC = EF Ср. Линия = (AE + EF + AE + EF) / 2 = AE + EF = AF а AF можно найти из треугольника ACF AF = AC / Корень(2) = ..

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Альтернативные методы решения геометрических задач. Трапеция.

Анализ представленных результатов и изучение опыта работы школы позволяют сделать некоторые выводы относительно состояния подготовки выпускников по курсу планиметрии:

– несмотря на некоторое повышение показателей за последние годы, общая тенденция низких результатов выполнения планиметрических задач не изменилась и, как и раньше, говорит о весьма слабой подготовке по планиметрии значительной части выпускников;

– небольшое повышение результатов, скорее всего, объясняется тем, что хотя и медленно, но все-таки ощутимо в практике работы школ усиливается внимание к геометрической подготовке выпускников. Особенно это проявляется среди более подготовленных учащихся.

Представленный мною материал окажет помощь при подготовке учащихся к ОГЭ в 9 классе и ЕГЭ в 11 классе по математике. Интересные свойства равнобедренной трапеции позволяют сэкономить время на экзамене и в значительной мере расширить свой кругозор учащихся в этой области.

В презентации представлены интересные свойства равнобедренной трапеции с доказательствами и решение некоторых задач двумя способами, один из которых с применением рассмотренных свойств. Наглядно показано, где более рационально решена задача.

Просмотр содержимого документа
«Задачи»

«ТРАПЕЦИЯ. РАЦИОНАЛЬНЫЕ ПРИЁМЫ РЕШЕНИЯ ЗАДАЧ».

Составитель: Сидорова А.В., МОУ СОШ № 31

Свойство . В равнобедренной трапеции проекция диагонали на большее основание равна средней линии трапеции.

В равнобедренной трапеции диагональ, равная 4 см, составляет с основанием угол 60°. Найдите среднюю линию трапеции. (Ответ: 2 см)

Площадь равнобедренной трапеции равна 32. Котангенс угла между диагоналями трапеции и её основанием равен 2. Найдите высоту трапеции. (Ответ: 4)

Боковая сторона равнобедренной трапеции равна , а основания равны 4 и 5. Найдите её диагональ. (Ответ: 14 )

В равнобокой трапеции основания 6 и 10. Диагональ равна 10. Найти площадь трапеции. (Ответ: 48)

Средняя линия равнобедренной трапеции равна 4. Площадь трапеции равна 8. Найти тангенс угла между диагональю и основанием трапеции. (Ответ: 0,5)

Найдите площадь равнобедренной трапеции, если её диагональ равна , а средняя линия равна 4. (Ответ: 24)

Найдите площадь равнобедренной трапеции, если её средняя линия равна 6, а тангенс угла между диагональю и основанием равен 1,5. (Ответ: 5 4)

Найти диагональ равнобедренной трапеции, если её площадь равна , а средняя линия равна 2. (Ответ: 6 )

Найти площадь равнобедренной трапеции, если её высота равна 4, а тангенс угла между диагональю и основанием равен . (Ответ: 96)

Найти площадь равнобедренной трапеции, если её диагональ, равная 13, образует с основанием угол, косинус которого равен . (Ответ: 78 )

Большее основание равнобедренной трапеции равно 8, боковая сторона 9, а диагональ 11. Найти меньшее основание. (Ответ: 5)

Меньшее основание равнобедренной трапеции равно 10, боковая сторона 18, а диагональ 22. Найти большее основание трапеции. (Ответ: 16)

Найти среднюю линию равнобедренной трапеции, если диагональ составляет угол 30° с основанием, а высота равна 2. (Ответ:)

В равнобедренной трапеции диагональ равна 13 см, а средняя линия – 12 см. Найдите высоту трапеции. (Ответ: 5)

Свойство . Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то её высота равна средней линии.

Свойство .Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты S = h 2 .

Диагонали равнобедренной трапеции взаимно перпендикулярны, а длина её средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции. (Ответ: 9)

В равнобедренной трапеции средняя линия равна 5, а диагонали взаимно перпендикулярны. Найдите площадь этой трапеции. (Ответ: 25)

Найти площадь равнобедренной трапеции, основания которой 12 и 34, а диагонали перпендикулярны. (Ответ: 529 )

В равнобедренной трапеции диагонали взаимно перпендикулярны. Найдите среднюю линию трапеции, если её площадь равна 36. (Ответ: 6)

Диагонали равнобедренной трапеции взаимно перпендикулярны, а её площадь равна 4. Найти высоту трапеции. (Ответ: 2)

Найти периметр равнобедренной трапеции, боковая сторона которой 13, высота 12, а диагонали взаимно перпендикулярны. (Ответ: 50)

Площадь равнобедренной трапеции равна 256, а диагонали взаимно перпендикулярны. Найдите среднюю линию трапеции. (Ответ: 18)

В равнобедренной трапеции ABCD (BC || AD) диагонали AC и BD взаимно перпендикулярны, ВС = 6 см, AD = 20 см. Найти длину отрезка, соединяющего середины оснований трапеции. (Ответ: 15)

В равнобедренной трапеции ABCD ( AD || BC ) Диагонали взаимно перпендикулярны, высота трапеции равна 12 см. Расстояние от вершины А до прямой CD в три раза больше, чем расстояние от вершины В до этой прямой. Найдите основания трапеции. (Ответ: 18 см и 6 см)

В окружность радиуса 5 вписана трапеция ABCD . Найдите длину средней линии трапеции, если известно, что её диагонали перпендикулярны друг другу, а синус угла ВАС равен 0,6. (Ответ: 7)

Свойство. Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии.

Около круга радиуса 2 см описана равнобедренная тра ­ пеция с острым углом 30°. Найти длину средней линии трапеции. (Ответ: 8)

Найти боковую сторону равнобокой трапеции, описанной около круга, если острый угол при основании трапеции равен , а площадь трапеции 288. (Ответ: 24)

Около окружности описана равнобочная трапеция, средняя линия которой равна 5, а синус острого угла при основании равен 0,8. Найдите площадь трапеции. (Ответ: 20)

Около окружности описана трапеция, площадь которой равна 20, а синусы углов при основании равны 0,8. Найти длину средней линии трапеции. (Ответ: 5)

Равнобедренная трапеция описана около окружности радиуса 5. Боковая сторона равна 12. Чему равна площадь трапеции? (Ответ: 120)

Равнобочная трапеция с площадью 40 и боковым ребром 8 такова, что в неё можно вписать окружность. Найти радиус окружности. (Ответ: 2,5)

Около окружности радиуса 2,5 описана равнобедренная трапеция. Площадь этой трапеции равна 40 . Чему равна боковая сторона трапеции? (Ответ: 8)

Площадь равнобедренной трапеции, описанной около окружности, равна 8. Найдите среднюю линию трапеции, если острый угол при её основании равен 30°. (Ответ: 4 )

Площадь равнобедренной трапеции, описанной около окружности, равна S, а высота трапеции в два раза меньше её боковой стороны. Найдите радиус окружности. (Ответ:)

В равнобедренную трапецию вписана окружность радиуса 4. Боковая сторона равна 9. Найти площадь трапеции. (Ответ: 72 )

В равнобедренной трапеции боковая сторона равна средней линии, а периметр равен 48. Найдите длину боковой стороны. (Ответ: 12)

В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности. (Ответ: 3)

Около круга описана равнобедренная трапеция, у которой средняя линия равна m . Определить периметр трапеции и длину её боковой стороны. (Ответ: Р = 4 m , боковая сторона m )

Найти радиус окружности, вписанной в равнобедренную трапецию, если средняя линия трапеции равна , а косинус угла при основании трапеции равен . (Ответ: 1,5)

Найти среднюю линию равнобедренной трапеции, описанной около окружности радиуса 2, если тангенс угла наклона при основании трапеции равен . (Ответ: 16)

Около круга радиуса 2 описана равнобедренная трапеция, периметр которой равен 20. Найти площадь этой трапеции. ( Ответ:20).

17. Около окружности радиуса r описана равнобочная трапеция, периметр которой равен 2р. Найдите большее основание трапеции. (Ответ: .)

В равнобочной трапеции, описанной около окружности, отношение оснований равно k. Найдите косинус угла при основании. (Ответ: )

Периметр равнобедренной трапеции вдвое больше длины вписанной окружности. Найти угол при основании трапеции.()

Равнобедренная трапеция описана около окружности радиуса 2. Найдите площадь трапеции, если косинус угла при большем основании трапеции равен 0,6. (Ответ: 40)

Площадь равнобедренной трапеции, описанной около окружности радиуса 3, равна 60. Найдите косинус угла при большем основании трапеции. (Ответ: 0,8)

Площадь равнобочной трапеции, описанной около круга, равна S, а высота трапеции в два раза меньше ее боковой стороны. Определить радиус вписанного круга. (Ответ: )

Свойство . Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований: h 2 = a ∙ b .

В равнобедренную трапецию с основаниями 18 см и 6 см вписан круг. Найдите его радиус и углы трапеции. (Ответ:)

Основания описанной около окружности равнобедренной трапеции равны 2 и 18. Найдите площадь трапеции. (Ответ: 60 )

Основания равнобедренной трапеции относятся как 1 : 5, а радиус окружности, вписанной в эту трапецию, равен 7,5 см. Найдите стороны трапеции. (Ответ:)

Около окружности с диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите основания трапеции. (Ответ: 25 и 9)

В равнобокую трапецию с верхним основанием, равным 1, вписана окружность единичного радиуса. Найти нижнее основание трапеции. (Ответ: 4)

Около окружности описана равнобедренная трапеция с боковой стороной l. Одно из оснований трапеции равно a. Найдите площадь трапеции. (Ответ:)

В равнобедренную трапецию вписана окружность радиуса 10. Верхнее основание трапеции в два раза меньше её высоты. Найдите площадь трапеции. (Ответ: 500)

В равнобочную трапецию вписана окружность радиуса R. Верхнее основание трапеции в два раза меньше ее высоты. Найти площадь трапеции. (Ответ: 5 R 2 )

В равнобокую трапецию вписана окружность радиуса 6 см, точка касания делит боковую сторону на отрезки, разность между которыми равна 5 см. Найти среднюю линию трапеции. (Ответ: 13)

Средняя линия равнобедренной трапеции равна 5 см. Известно, что средняя линия делит площадь трапеции на две части, площади которых относятся как 7:13. Найти высоту трапеции, если известно, что в неё можно вписать окружность. (Ответ: 4)

Около окружности описана равнобочная трапеция BCDE (CD || BE) площадь которой равна , CD : ВЕ = 1 : 2. Найти ВС. (Ответ: 1)

Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно а, а угол при меньшем основании равен 120°.(Ответ:.)

В равнобедренную трапецию вписан круг. Боковая сторона делится точкой касания на отрезки длиной 9 и 16. Определить площадь трапеции. (Ответ: 600)

Около окружности, радиус которой равен 10, описана равнобедренная трапеция. Расстояния между точками касания окружности с боковыми сторонами трапеции 12. Найдите боковую сторону трапеции. (Ответ: )

Средняя линия равнобокой трапеции, описанной около круга, равна 68. Найти радиус этого круга, если нижнее основание трапеции больше верхнего на 64. (Ответ: 30)

В равнобедренную трапецию, большее основание которой равно 36, вписана окружность радиуса 12. Найдите наименьшее основание трапеции. (Ответ: 16)

В равнобедренную трапецию, длины оснований которой равны и , можно вписать окружность. Найдите длину диагонали этой трапеции. (Ответ: 2,5)

Окружность радиуса 12 вписана в равнобедренную трапецию. Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4. Найдите периметр трапеции. (Ответ: 120).

В равнобедренную трапецию, у которой одно основание в 4 раза меньше другого, вписана окружность. Докажите, что радиус этой окружности равен меньшему основанию.

Разные задачи по теме «Трапеция»

Диагональ равнобочной трапеции делит тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции. (Ответ: 96)

Доказать, что площадь трапеции равна произведению одной из непараллельных сторон на перпендикуляр, опущенный из середины другой непараллельной стороны на первую.

Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно . Найдите углы трапеции. (Ответ: )

В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции. (Ответ: 30,72)

В равнобедренной трапеции диагональ перпендикулярна боковой стороне, а меньшее основание равно b. Найдите боковую сторону, если известно, что она в m раз короче диагонали.

В равнобедренной трапеции диагональ перпендикулярна боковой стороне, а длина диагонали равна d. Найдите меньшее основание, если известно, что большее основание в m раз длиннее боковой стороны.

Около окружности радиуса R описана прямоугольная трапеция площади S. Вычислите острый угол трапеции. (Ответ: .)

Найдите площадь равнобедренной тапеции, зная длину ее диагонали 10 см и величину угла в 15 ⁰ между этой диагональю и большим основанием. (Ответ: 25.)

Основания BC и AD равнобедренной трапеции ABCD равны 4 и 8 соответственно. В трапеции проведены две высоты СН и BN . Диагональ АС пересекает высоту BN в точке О и равна . Найдите длину отрезка ON . (Ответ: 1.)

Периметр равнобедренной трапеции равен 136. Известно, что в эту трапецию можно вписать окружность, причём боковая сторона делится точкой касания в отношении 9 : 25. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найти отношение площади этого треугольника к площади трапеции. (ЕГЭ -2011)

(Ответ: .)

Трапеция с основаниями 14 и 30 вписана в окружность радиуса 25. Найдите высоту трапеции. (Ответ: 39 или 9)

В окружность радиуса вписана трапеция с основаниями 8 и . Найдите длину диагонали трапеции. (Ответ: .)

Трапеция ABCD с основаниями AD и ВС вписана окружность с центром О , Найдите высоту трапеции, если ее средняя линия равна 3 и . (Ответ: 9 или 1)

Трапеция ABCD с основаниями AD = 6, ВС = 4 и диагональю BD = 7 вписана в окружность. На окружности взята точка К , отличная от точки D так, что ВК = 7. Найдите длину отрезка АК . (Ответ: 4).

В равнобокой трапеции ABCD основания AD и ВС равны 20 и 8 соответственно, а боковая сторона равна 10. Через вершину А проведена прямая, делящая площадь трапеции в отношении 1 : 3 и пересекающая прямую ВС в точке К. Найдите длину отрезка КС. (Ответ: 1 или .)

Сборник задач по математике для поступающих в вузы. Геометрия/ Под ред. М.И.Сканави.- М.: Издательский дом ОНИКС: Альянс-В, 1999.

Зив Б.Г. ,Мейлер В.М. , Баханский А.Г. . Задачи по геометрии для 7-11 классов -М.: Просвещение, 1991.

Денищева Л.О., Глазков Ю.А., Краснянская К.А. и др. Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Математика.- М: Интеллект- Центр, 2003-2008.

Кочагин В.В., Бойченко Е.М., Глазков Ю.А. и др. ЕГЭ- 2008: математика: реальные задания.- М.: АСТ: Астрель, 2008.

Ковалева Г.И., Бузулина Т.И., Безрукова О.Л., Розка Ю.А. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов.- Волгоград: Учитель, 2007.

Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. Система тренировочных задач и упражнений по математике.- М.: Просвещение, 1991.

Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по геометрии для 8 класса.- М.: Илекса, Харьков: Гимназия, 1999.

Атанасян Л.С., Бутузов В.Ф. и др. Геометрия: Учеб. для 7-9 кл. сред.шк.- М.: Просвещение, 1991.

Прокофьев А.А., Корянов А.Г. Планиметрические задачи с неоднозначностью в условии (многовариантные задачи) (типовые задания С4)

Просмотр содержимого презентации
«альтернативные методы решения геометрических задач ГИА и ЕГЭ»

Углы при одном основании трапеции равны 37⁰ и 53⁰, отрезки, соединяющие середины противоположных сторон, равны 21 и 12. Найдите основания трапеции. (ОГЭ)

BN = NC, AM = MD, EF = 21, NM = 12

• Диагонали трапеции разбивают её на четыре треугольника, причём треугольники, прилежащие к основаниям, подобны друг к другу, а треугольники, прилежащие к боковым сторонам, равновеликие, т.е. имеют равные площади.

• Отрезок разбивающий трапецию на две подобные

трапеции, имеет длину равную

• В любой трапеции следующие четыре

точки лежат на одной прямой: середины

оснований, точка пересечения диагоналей,

точка пересечения продолжений боковых

• Отрезок, параллельный основаниям трапеции, походящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам.

Его длина есть среднее гармоническое

• Если в трапецию вписана окружность,

то отрезки, соединяющие центр

окружности с концами боковой стороны

• Если в трапецию вписана окружность и m , n , p , q — длины отрезков боковых сторон от точек касания до вершин,

то для вычисления радиуса вписанной в неё окружности

можно использовать формулы:

• В равнобедренной трапеции углы при любом основании равны.
• В равнобедренной трапеции длины диагоналей равны.
• В равнобедренной трапеции, прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
• Если трапецию можно вписать в окружность, то она равнобедренная.

Найдите площадь равнобедренной трапеции, если её диагональ, равная 10, образует с основанием угол, косинус которого равен . (ГИА)

В равнобедренной трапеции проекция диагонали на большее основание равна средней линии трапеции.

Найдите площадь равнобедренной трапеции, если её диагональ, равная 10, образует с основанием угол, косинус которого равен .

В равнобедренной трапеции диагонали взаимно перпендикулярны. Найдите площадь трапеции, основания которой равны 10 и 26. (ГИА)

2) Проведём высоту МК;

AK =OK = 13, BM = MO = 5, MK = 18

Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то её высота равна средней линии.

AB = CD, AC BD, BH – высота

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты, т.е. .

AB = CD , BH – высота трапеции

В равнобедренной трапеции диагонали взаимно перпендикулярны. Найдите площадь трапеции, основания которой равны 10 и 26.

Найдите радиус окружности, если основания описанной около неё равнобедренной трапеции равны 4 см и 16 см.

AD = 16 cм, ВС = 4 см

Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии трапеции.

по свойству четырёхугольника, описанного около окружности:

AB + CD = AD + BC, AB = CD,

Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований: .

в трапецию ABCD

h – высота трапеции

1)По свойству отрезков касательных,

проведённых из одной точки к

2)Проведём высоту ВН и рассмотрим

AD = 16 cм, ВС = 4 см

Равнобедренная трапеция описана около круга. Боковая сторона трапеции делится точкой касания на отрезки длиной 18 и 32. Найдите площадь трапеции. (ГИА)

Дано : окр.( О ; r ) вписана в трапецию ABCD

5) S = 50 · 36 = 1800

Около круга радиуса r описана равнобедренная трапеция. Боковая сторона трапеции составляет с меньшим основанием угол α. Найдите радиус круга, описанного около трапеции.

описанная около окр.( О ; r ) и вписанная в окр.( О 1 ;R ) AB = CD ,

по теореме синусов

В описанной около окружности равнобокой трапеции основания относятся как 3 : 5. Из вершины меньшего основания опущена высота на большее основание; точка Н – основание высоты. Из точки Н опущен перпендикуляр НЕ на боковую сторону трапеции. В каком отношении точка Е делит боковую сторону? (ЕГЭ, С4)

Дано : окр.( О ; r ) вписана в трапецию ABCD

• Пусть k- коэффициент пропорциональности, тогда

(по двум углам)

• (по гипотенузе и острому углу)

Ответ: а) 1 : 15; б) 1 : 3.

• Сборник задач по математике для поступающих в вузы. Геометрия/ Под ред. М.И.Сканави.- М.: Издательский дом ОНИКС: Альянс-В, 1999.
• Зив Б.Г. ,Мейлер В.М. , Баханский А.Г. . Задачи по геометрии для 7-11 классов -М.: Просвещение, 1991.
• Денищева Л.О., Глазков Ю.А., Краснянская К.А. и др. Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Математика.- М: Интеллект- Центр, 2003-2008.
• Кочагин В.В., Бойченко Е.М., Глазков Ю.А. и др. ЕГЭ- 2008: математика: реальные задания.- М.: АСТ: Астрель, 2008.
• Ковалева Г.И., Бузулина Т.И., Безрукова О.Л., Розка Ю.А. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов.- Волгоград: Учитель, 2007.
• Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. Система тренировочных задач и упражнений по математике.- М.: Просвещение, 1991.
• Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по геометрии для 8 класса.- М.: Илекса, Харьков: Гимназия, 1999.
• Атанасян Л.С., Бутузов В.Ф. и др. Геометрия: Учеб. для 7-9 кл. сред.шк.- М.: Просвещение, 2008.
• Математика ЕГЭ- 2008. Вступительные испытания.Под ред. Ф.Ф.Лысенко.- Ростов-на-Дону: Легион, 2008.
• Прокофьев А.А., Корянов А.Г. Планиметрические задачи с неоднозначностью в условии (многовариантные задачи) (типовые задания С4)
• http://www-formula.ru/index.php/2011-09-19-02-39-24/trapeze-area
• http://isu.ru/ru/egevic/mathematics/planimetry/opornye_zadachi_planimetrii.pdf

ABNK и NCDF — параллелограммы

при AB || NK и секущей АК);

при СD || NF и секущей АК)

Δ KNF – прямоугольный, MN — медиана

где KF = AD – (AK + FD) = AD — BC

Если в трапецию ABCD вписана окружность c центром О ,

Дано : окр.( О ; r ) вписана в трапецию ABCD

• AO OD ;

Радиус окружности, описанной около трапеции, равен радиусу окружности, описанной около треугольника, вершины которого лежат в вершинах данной трапеции.

📹 Видео

Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать

Радиус описанной окружности трапецииСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Планиметрия 38 | mathus.ru | окружность вписана в равнобедрунную трапецию | отношение площадейСкачать