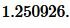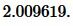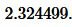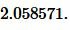Геометрия | 5 — 9 классы
В равнобедренный треугольник с основанием 40 см вписана окружность.
Высота, проведенная к основанию, равна 15 см.
Найдите расстояние между точками касания окружности с боковыми сторонами треугольника.
Подробнее на чертеже в приложении.
Пожалуйста, с полным решением и пояснениями!
Решение , чертеж в приложении.
- В окружность радиуса 10 вписан равнобедренный треугольник?
- В равнобедренный треугольник вписана окружность?
- Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см?
- Основание равнобедренного треугольника равно 6, боковая сторона 9?
- ПОМОГИТЕЕЕЕ?
- . В равнобедренном треугольнике у которого боковая сторона равна 10см, а основание 6см вписана в окружность?
- ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА?
- 21. Основание равнобедренного треугольника равно 40 см, а высота, проведенная к нему, — 15 см?
- Помогите пожалуйста, очень надо В равнобедренный треугольник с основанием 40 см вписана окружность?
- Боковая сторона равнобедреного треугольника в котором вписана окружность равна 50 см высота это го же проведеная к основанию равна 40 см?
- В равнобедренный треугольник с основание 40 см вписана окружность
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- 🎥 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В окружность радиуса 10 вписан равнобедренный треугольник?
В окружность радиуса 10 вписан равнобедренный треугольник.
Высота треугольника, проведенная к основанию, в сумме с основанием дает диаметр окружности.
Найдите основание треугольника.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

В равнобедренный треугольник вписана окружность?
В равнобедренный треугольник вписана окружность.
Точка касания этой окружности делит боковую сторону на отрещки 6и8см, считая от основания найдите периметр треугольника хелп.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см?
Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см.
Найдите плщадь этого треугольника и его боковую сторону.
Видео:№108. Периметр равнобедренного треугольника ABC с основанием ВС равен 40 см, а периметрСкачать

Основание равнобедренного треугольника равно 6, боковая сторона 9?
Основание равнобедренного треугольника равно 6, боковая сторона 9.
В треугольник вписана окружность.
Найти расстояние между точками касания, лежащими на боковых сторонах треугольника.
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

ПОМОГИТЕЕЕЕ?
В равнобедренный треугольник вписана окружность, точка касания этой окружности делит одну из боковых сторон на отрезки, равные 6 см и 8см, считая от основания.
Найдите периметр треугольника.
Видео:Равнобедренный треугольник. 7 класс.Скачать

. В равнобедренном треугольнике у которого боковая сторона равна 10см, а основание 6см вписана в окружность?
. В равнобедренном треугольнике у которого боковая сторона равна 10см, а основание 6см вписана в окружность.
Определить расстояние между точками касания находящиеся на его боковых сторонах.
Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА?
ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА!
В равнобедренный треугольник с боковой стороной 10см и высотой, проведённой к основанию, 8см вписана окружность.
Найти длину отрезка, соединяющего точки касания окружности с боковыми сторонами.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

21. Основание равнобедренного треугольника равно 40 см, а высота, проведенная к нему, — 15 см?
21. Основание равнобедренного треугольника равно 40 см, а высота, проведенная к нему, — 15 см.
Найдите расстояние между точками касания окружности, вписанной в треугольник, с его боковыми сторонами.
22. Боковая сторона равнобедренного треугольника равна 40 см, а высота, проведенная к основанию, – 4√91 см.
Найдите расстояние между точками пересечения биссектрис углов при основании треугольника с его боковыми сторонами.
Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Помогите пожалуйста, очень надо В равнобедренный треугольник с основанием 40 см вписана окружность?
Помогите пожалуйста, очень надо В равнобедренный треугольник с основанием 40 см вписана окружность.
Высота, проведенная к основанию, равна 15 см.
Найдите расстояние между точками касания.
Видео:№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

Боковая сторона равнобедреного треугольника в котором вписана окружность равна 50 см высота это го же проведеная к основанию равна 40 см?
Боковая сторона равнобедреного треугольника в котором вписана окружность равна 50 см высота это го же проведеная к основанию равна 40 см.
Найти расстояние между точками касания окружности с боковыми сторонами треугольника.
На этой странице находится вопрос В равнобедренный треугольник с основанием 40 см вписана окружность?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
1)120•2 = 240(действие в скопках, умножение первое) 2)240 / 40 = 6(действие в скопках, деление второе) 3)6 + 144 = 150(действие в скопках, сумма третья) 4)150 / 6 = 25(действие за скопками, четвёртое деление).
По условию (см. Фото) : О — центр сферы, ОА — радиус сферы. О1 — центр секущей плоскости, АО1 — радиус секущей плоскости r. ОО1 — расстояние от центра сферы до секущей плоскости, равное 3 см. С1 обозначим длину окружности секущей плоскости. С1 =..
Если угол 150, то острые углы по 30 град, проведенные высоты образуют треугольники прямоугольные. Их свойство — катет против угла в 30 град равен половине гипотенузы. Гипотенузы — стороны параллелограмма, значит 2m и 2n cоотаетственно.
Вот, надеюсь поймешь, камера ужасная.
56 — 24 = 32 32 / 2 = 16 24 / 2 = 12 Ответ : 12, 12, 16, 16.
Периметр параллелограммаравен удвоенной сумме 2 — х его сторон или : Р = 2а + 2в. По условию мы знаем 2а = 24смПериметр Р = 56см. Подставим эти значения в формулу : 24 + 2в = 562в = 56 — 242в = 32в = 32 : 2в = 16 см — 1из других сторон. 2а = 24а =..
1. DO = BD / 2 = 9 2. AC = 2 * BO = 22 3. ∠ACD = (180° — 84°) / 2 = 48°.
Соs120° = — 0, 5. Скалярное произведение равно 3·4·(0, 5) = — 6.
Противоположные стороны прямоугольника равны. Периметр прямоугольника находят по формуле Р = 2(а + b), где a и b — стороны прямоугольника, Р — его периметр. Пусть меньшая сторона прямоугольника х см, тогда большая сторона прямоугольника равна (2х) ..
Ответ 28, 28 Сторону берем за Х. И по теореме пифагора находим эту сторону. Так как у на сквадрат то получаем Х ^ 2 + X ^ 2 = 10 ^ 2. 2X ^ 2 = 100. X ^ 2 = 50. Х = корню из 50. Х = 5 корней из 2. Ну а дальше все просто.
Видео:Геометрия В равнобедренный треугольник вписана окружность Точка касания делит боковую сторонуСкачать

В равнобедренный треугольник с основание 40 см вписана окружность
Боковые стороны равнобедренного треугольника равны 104, основание равно 192. Найдите радиус описанной окружности этого треугольника.
Для нахождения площади треугольника ABC воспользуемся формулой Герона:
Далее по формуле
Боковые стороны равнобедренного треугольника равны 30, основание равно 36. Найдите радиус описанной окружности этого треугольника.
Найдем площадь треугольника по формуле Герона:
Далее по формуле имеем:
Приведем решение Александры Саяпиной.
Пусть AB — основание равнобедренного треугольника. По теореме косинусов найдем косинус угла A:
следовательно, Тогда по теореме синусов
откуда
Боковые стороны равнобедренного треугольника равны 13, основание равно 24. Найдите радиус описанной около этого треугольника окружности.
Чтобы найти площадь треугольника ABC, воспользуемся формулой Герона:
Далее по формуле находим:
Приведем еще одно решение.
Проведем высоту CH прямоугольного треугольника ACH и найдем ее:
Следовательно,
Применим теорему синусов к треугольнику ABC, получим откуда
Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.
Это задание ещё не решено, приводим решение прототипа.
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
Чтобы найти площадь треугольника ABC, воспользуемся формулой Герона:
Далее по формуле находим:
Приведем еще одно решение.
Проведем высоту CH прямоугольного треугольника ACH и найдем ее:
Следовательно,
Применим теорему синусов к треугольнику ABC, получим откуда
Приведем решение Павла Юкляева.
Треугольник ABC является остроугольным, поскольку 48 2 2 + 40 2 . В равнобедренном остроугольном треугольнике центр описанной окружности О лежит на высоте, проведенной к основанию.
Проведем высоту CH, найдем ее из прямоугольного треугольника ACH:
Из прямоугольного треугольника AOH получим:
а тогда
Приведем решение Артема Абросимова.
Запишем теорему косинусов:
Далее подставим числа:
Зная, найдем
Отрезки AO и OC равны искомому радиусу описанной окружности R, поэтому по теореме косинусов для треугольника AOC получаем:
откуда, подставляя числа, заключаем:
Таким образом, следовательно,
Еще одно решение приведено в задаче 53843.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Геометрия В равнобедренный треугольник с углом 120 при вершине и боковой стороной а вписанаСкачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
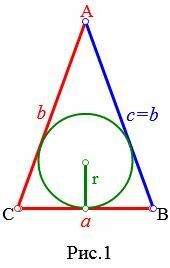 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
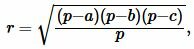 | (1) |
где полупериметр p вычисляется из формулы:
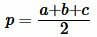 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac, ) | (3) |
| ( small p-a=frac-a ) ( small =frac, ) | (4) |
| ( small p-b=p-c=frac-b ) ( small =frac. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
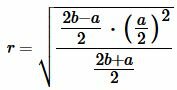 , , |
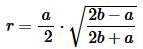 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
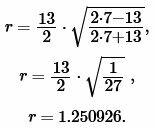 |
Ответ:
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
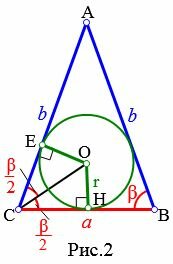 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:
| ( small frac=frac<large frac>=mathrmfrac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrmfrac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
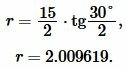 |
Ответ:
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
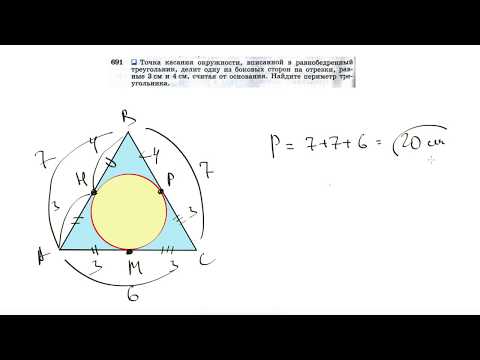
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
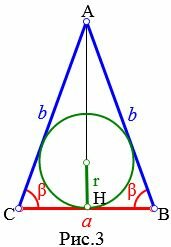 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac=frac<large frac>= cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac ) |
| ( small r=b cdot cos beta cdot mathrmfrac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
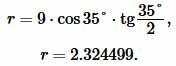 |
Ответ:
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
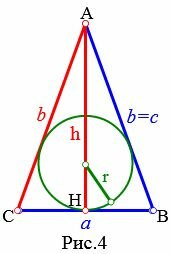 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
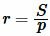 , , | (13) |
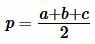 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( fracright)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
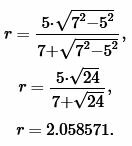 |
Ответ:
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
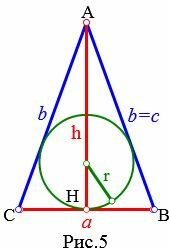 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >) |
| ( small r=large frac<a+ sqrt>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
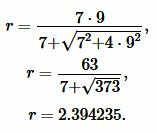 |
Ответ:
🎥 Видео
Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Планиметрия 39-40 | mathus.ru | четырехугольник отсекается от равнобедренного треугольника прямойСкачать