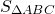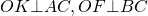В прямоугольный треугольник ABC вписана окружность, которая касается гипотенузы AB в точке K, а катетов — в точках P и M.
а) Докажите, что площадь треугольника ABC равна AK · BK.
б) Найдите площадь треугольника PKM, если известно, что AK = 12, BK = 5.
а) Пусть O — центр окружности, вписанной в треугольник ABC, r — радиус этой окружности, P ∈ BC, M ∈ AC. Соединим О с вершинами треугольника А, В и С.
Докажем, что CMOP — квадрат.
По свойству касательной к окружности: OP ⊥ BC, OM ⊥ AC. Следовательно, MC || OP, OM || CP, значит, CMOP — параллелограмм.
CMOP — параллелограмм, ∠P = 90°, значит, CMOP — прямоугольник, CMOP — прямоугольник, OM = OP = r, значит, CMOP — квадрат.
По свойству касательных к окружности, проведенных из одной точки: BK = BP, AK = AM, MC = CP.
То есть 2S(ABC) = AK · BK + S(ABC), откуда: S(ABC) = AK · BK, что и требовалось доказать.
б) Соединим точки M и K, M и P, P и K отрезками. Найдем r.
Но как было доказано выше, S(ABC)=AK · BK = 60. Следовательно,
Пусть ∠BAC = α, тогда:
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать 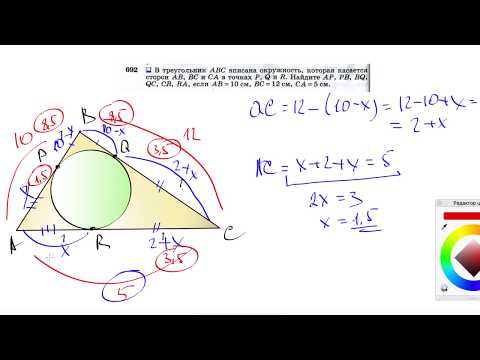 Задача 44827 В прямоугольный треугольник ABC с прямым.УсловиеВ прямоугольный треугольник ABC с прямым углом C вписана окружность, касающаяся строн треугольника в точках D,E,K. Найти площадь треугольника DEK, если BC=8,AC = 6 Все решенияПо теореме Пифагора гипотенуза АВ=10 Эта же самая окружность описана около ΔDEK Осталось найти стороны треугольника ΔDEK DK=2sqrt(2) из Δ CDK ( равнобедренного прямоугольного) Тогда Из Δ AKE по теореме косинусов =6*sqrt(2)*sqrt(0,32)=[b]4,8[/b] Видео:🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Узнать ещёЗнание — сила. Познавательная информация Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать 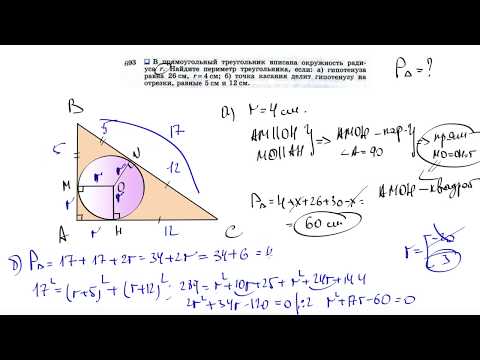 Окружность, вписанная в прямоугольный треугольникЕсли в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора. Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле где a и b — длины катетов, c — гипотенузы. Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность. Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности. окружность (O, r) — вписанная, K, M, F — точки касания со сторонами AC, AB, BC, 1) По свойству отрезков касательных, проведенных из одной точки,
2) AB=AM+BM=6+4=10 см, 3) По теореме Пифагора: Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см. Ответ: 24 см, 24 см², 2 см. Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.
окружность (O, r) — вписанная, K, M, F — точки касания со сторонами AC, AB, BC, 1) Проведем отрезки OK и OF. (как радиусы, проведенные в точки касания). Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые). А так как OK=OF (как радиусы), то OKCF — квадрат. 2) По свойству касательных, проведенных из одной точки, 3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см. 🎬 ВидеоВ треугольник АВС вписана окружность, которая касается АВ в точке РСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  Вписанный в окружность прямоугольный треугольник.Скачать  В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  ✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать  В прямоугольный треугольник вписана окружность. Этап 3Скачать  Окружность вписана в прямоугольный треугольник и касается его средней линии, найти RСкачать  В прямоугольный треугольник вписана окружность. Этап 7Скачать  В прямоугольный треугольник вписана окружность. Этап 8Скачать  №694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать  Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать  В прямоугольный треугольник вписана окружность. Найти радиусСкачать  Геометрия Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВСкачать  В прямоугольный треугольник вписана окружность. Этап 2Скачать  В прямоугольный треугольник вписана окружность. Этап 6Скачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Строим вписанную в данный треугольник окружность (Задача 2).Скачать  |
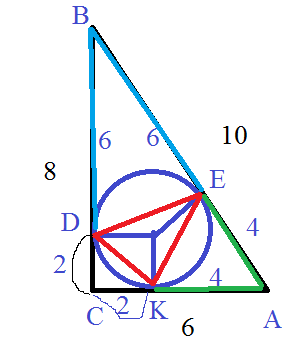
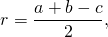
 Дано: ∆ ABC, ∠C=90º,
Дано: ∆ ABC, ∠C=90º,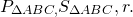
 AK=AM=6 см,
AK=AM=6 см,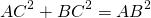
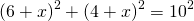
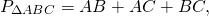
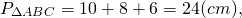
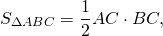
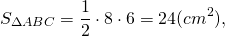
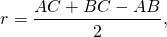
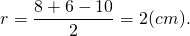
 Дано:∆ ABC, ∠C=90º,
Дано:∆ ABC, ∠C=90º,