- Ваш ответ
- решение вопроса
- Похожие вопросы
- Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
- Принятые в формулах обозначения
- Найти периметр трапеции
- Основные свойства равнобедренной трапеции
- Формулы длин сторон равнобедренной трапеции:
- Формулы длины средней линии равнобедренной трапеции:
- Формулы определения длины высоты равнобедренной трапеции:
- В исходных данных: все стороны
- Периметр произвольной трапеции
- Вписанная окружность
- Решение задач о прямоугольной трапеции
- Задача Даны три стороны, одна из которых перпендикулярная боковая.
- Задача Даны оба основания и угол при основании
- Свойства и признаки равнобедренной трапеции
- Формула определения радиуса вписанной в трапецию окружности
- Формулы определения длин отрезков проходящих через трапецию:
- Определение периметра прямоугольной трапеции
- Известны: диагонали и углы между ними
- Решение №2462 Около трапеции описана окружность. Периметр трапеции равен 38 …
- 💥 Видео
Видео:Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Ваш ответ
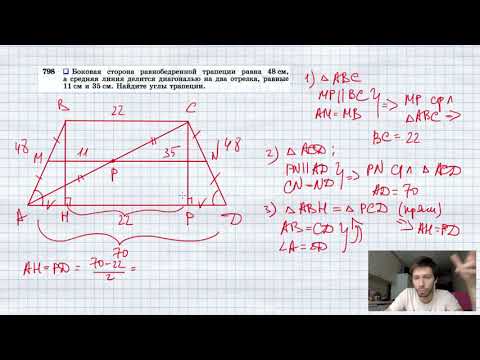
Видео:№798. Боковая сторона равнобедренной трапеции равна 48 см, а средняя линия делится диагональю на дваСкачать
решение вопроса
Видео:Периметр прямоуг. трапеции, описанной около окружн., равен 100, ее большая боковая сторона равна 37.Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,006
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
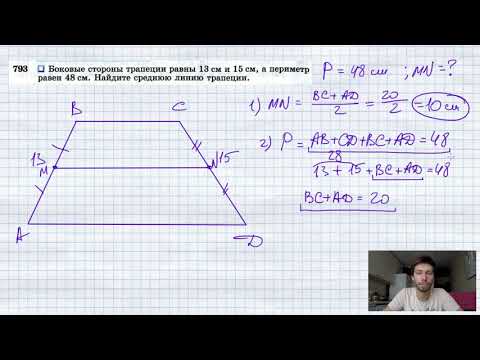
Видео:№793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линиюСкачать
Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
Видео:ЕГЭ Математика Задание 6#27938Скачать
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Найти периметр трапеции

| a = |
| b = |
| c = |
| d = |
Вводить можно числа или дроби (-2.4, 5/7, …).
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Видео:Боковая сторона равнобедренной трапеции равна ее меньшему основаниюСкачать

В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 – (((а – в) 2 + с 2 – d 2 )/(2(а – в))) 2 ). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с 2 – (а – в) 2 /4). Номер 2.
Видео:Задача 6 №27834 ЕГЭ по математике. Урок 100Скачать

Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a , BC=b , CD=c , AD=d , имеет вид:
[ LARGE P_ = a + b + c + d ]
где:
P – периметр трапеции
a, b, c, d – стороны трапеции
Видео:2119 периметр прямоугольной трапеции описанной около окружности равен 100 её большаяСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом 



Видео:№599. Найдите площадь равнобедренной трапеции с основаниями 2 см и 6 см, если уголСкачать

Решение задач о прямоугольной трапеции
Прямоугольной называют трапецию, у которой углы при одной из боковых сторон равны 90 0 . Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Задача Даны три стороны, одна из которых перпендикулярная боковая.
Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.
Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.
Находим отрезок КД:
- КД = АД – АК = 6 – 1 = 5 (см)
Согласно теореме Пифагора:
- СД 2 =СК 2 +КД 2 =12 2 +5 2 =144+25=169
- СД = √169 = 13 (см)
Ответ: СД = 13 см
Задача Даны оба основания и угол при основании
Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов. Найдите меньшую боковую сторону.
- Проводим высоту СК и получаем прямоугольный треугольник СКД и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
- КД = АД – АК = 10 – 6 = 4 см
- cos 45 = √2/2 = КД / СД, отсюда СД = КД / cos 45
- Получаем СД = 4/√2/2 = 4√2 (см)
Ответ: СД = 4√2 см
Видео:Радиус описанной окружности трапецииСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Видео:Трапеция. Свойства. Задачи. Найти углы трапеции. ПериметрСкачать

Определение периметра прямоугольной трапеции
Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:
Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.
- опустим высоту из вершины С, высота CH = AB = 5см;
- исходя из рисунка 3, AH = BC = 7 см;
- HD = AD – AH = 10 – 7 = 3 см;
- далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
- подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.
Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:
- формула расчета длины основания через среднюю линию;
- формулы длин сторон через высоту и угол при нижнем основании трапеции;
- формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
- формулы длин сторон равнобедренной трапеции через площадь.
Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.
Видео:✓ Радиус описанной окружности | ЕГЭ. Задание 1. Математика. Профильный уровень | Борис ТрушинСкачать

Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d1 2 * sin γ) / (а + в) или н = (d1 2 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1 2 * sin γ) / 2m или н = (d1 2 * sin δ) / 2m. Номер 6а.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

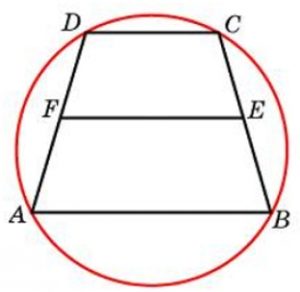
Решение №2462 Около трапеции описана окружность. Периметр трапеции равен 38 …
Около трапеции описана окружность. Периметр трапеции равен 38, средняя линия равна 11. Найдите боковую сторону трапеции.
Источник: Ященко ЕГЭ 2022 (36 вар)
Средняя линия трапеции равна полусумме её оснований:
DC + AB = 2·11 = 22
Зная периметр, найдём сумму боковых сторон:
DA + CD = PABCD – (DC + AB) = 38 – 22 = 16
В окружность можно вписать только равнобедренную трапецию:
DA = CD = 16/2 = 8
💥 Видео
Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

2113 Боковые стороны трапеции описанной около окружности равны 16 и 3 Найдите среднюю линию трапецииСкачать

Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

8 класс, 6 урок, ТрапецияСкачать