В прямоугольный треугольник abc вписана окружность которая касается

Условие

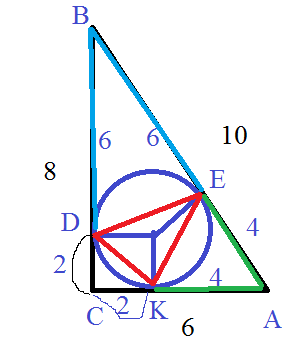
В прямоугольный треугольник ABC с прямым углом C вписана окружность, касающаяся строн треугольника в точках D,E,K. Найти площадь треугольника DEK, если BC=8,AC = 6

Все решения

По теореме Пифагора гипотенуза АВ=10
Радиус вписанной окружности :
r=(a+b-c)/2=(8+6-10)/2=2

Эта же самая окружность описана около ΔDEK

Осталось найти стороны треугольника ΔDEK

DK=2sqrt(2) из Δ CDK ( равнобедренного прямоугольного)

Тогда
Из Δ DBE по теореме косинусов
DE^2=6^2+6^2-2*6*6*cos ∠ B=72-72*0,6=72*(1-0,6)=72*0,4
DE=6*sqrt(0,8)

Из Δ AKE по теореме косинусов
KE^2=4^2+4^2-2*4*4*cos ∠ A=32-32*0,8=32*(1-0,8)=32*0,2
KE=4*sqrt(0,4)

=6*sqrt(2)*sqrt(0,32)=[b]4,8[/b]

Видео:№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

В прямоугольный треугольник abc вписана окружность которая касается

В прямоугольный треугольник ABC вписана окружность, которая касается гипотенузы AB в точке K, а катетов — в точках P и M.

а) Докажите, что площадь треугольника ABC равна AK · BK.

б) Найдите площадь треугольника PKM, если известно, что AK = 12, BK = 5.

а) Пусть O — центр окружности, вписанной в треугольник ABC, r — радиус этой окружности, P ∈ BC, M ∈ AC. Соединим О с вершинами треугольника А, В и С.

Докажем, что CMOP — квадрат.

По свойству касательной к окружности: OP ⊥ BC, OM ⊥ AC. Следовательно, MC || OP, OM || CP, значит, CMOP — параллелограмм.

CMOP — параллелограмм, ∠P = 90°, значит, CMOP — прямоугольник, CMOP — прямоугольник, OM = OP = r, значит, CMOP — квадрат.

По свойству касательных к окружности, проведенных из одной точки: BK = BP, AK = AM, MC = CP.

То есть 2S(ABC) = AK · BK + S(ABC), откуда: S(ABC) = AK · BK, что и требовалось доказать.

б) Соединим точки M и K, M и P, P и K отрезками. Найдем r.

Но как было доказано выше, S(ABC)=AK · BK = 60. Следовательно,

Пусть ∠BAC = α, тогда:

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.	3
Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.	2
Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:В треугольник АВС вписана окружность, которая касается АВ в точке РСкачать 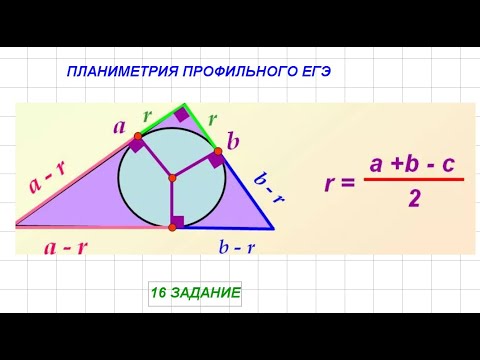В прямоугольном треугольнике ABC ZC = 90°, A = 60°. В этот треугольник вписана окружность, которая касается сторон АВ, ВС и АС соответственно Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать 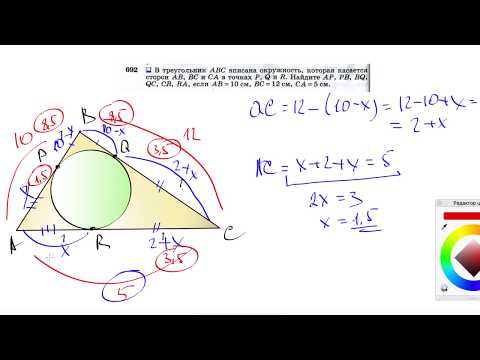Ваш ответ Видео:2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать решение вопроса Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать Похожие вопросы Все категории экономические 43,282 гуманитарные 33,619 юридические 17,900 школьный раздел 607,006 разное 16,829 Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 🎥 Видео №693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать 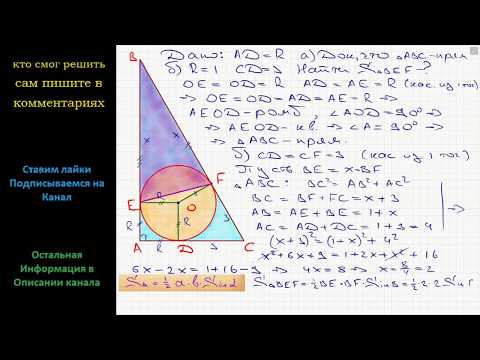🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать №412. Даны равнобедренный прямоугольный треугольник ABC с прямым углом С, катетом АС = 12 смСкачать Всё про углы в окружности. Геометрия | МатематикаСкачать Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать Геометрия Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВСкачать Задача о треугольнике из тренировочного варианта ЕГЭСкачать Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать Задание 16 ЕГЭ вариант №121Скачать ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать №694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать Вписанный в окружность прямоугольный треугольник.Скачать ОГЭ, геометрия, задачи повышенной сложности. Часть 3Скачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности