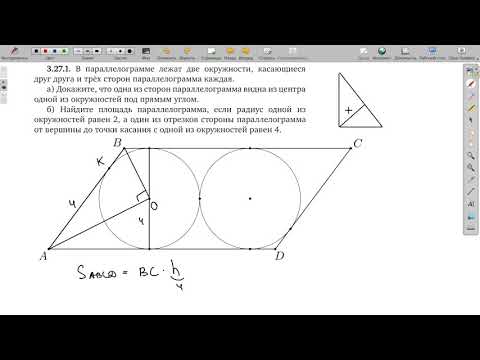
В параллелограмме лежат две окружности одна из них радиуса 3

Видео:3.27.1. Планиметрия. Гордин Р.К.Скачать

Разделы

Видео:Сможешь найти площадь параллелограмма? Внутри него есть две окружностиСкачать

Дополнительно

Задача по математике — 4162

Две окружности касаются друг друга внешним образом в точке $C$. Радиусы окружностей равны 2 и 7. Общая касательная к обеим окружностям, проведённая через точку $C$, пересекается с другой их общей касательной в точке $D$. Найдите расстояние от центра меньшей окружности до точки $D$.

Задача по математике — 4163

Теорема Брахмагупты. Диагонали вписанного четырёхугольника перпендикулярны и пересекаются в точке $P$. Докажите, что прямая, проходящая через точку $P$ и перпендикулярная одной из сторон четырёхугольника, делит противоположную сторону пополам.

Задача по математике — 4164

Две окружности касаются друг друга внешним образом в точке $A$. Найдите радиусы окружностей, если хорды, соединяющие точку $A$ с точками касания с одной из общих внешних касательных, равны 6 и 8.

Задача по математике — 4165

Найдите отношение радиусов двух окружностей, касающихся между собой, если каждая из них касается сторон угла, равного $alpha$.

Задача по математике — 4166

В острый угол, равный $60^$, вписаны две окружности, касающиеся друг друга внешним образом. Радиус меньшей окружности равен $r$. Найдите радиус большей окружности.

Задача по математике — 4167

В равнобедренной трапеции лежат две окружности. Одна из них, радиуса 1, вписана в трапецию, а вторая касается двух сторон трапеции и первой окружности. Расстояние от вершины угла, образованного двумя сторонами трапеции, касающимися второй окружности, до точки касания окружностей вдвое больше диаметра второй окружности. Найдите площадь трапеции.

Задача по математике — 4168

В параллелограмме лежат две окружности. Одна из них, радиуса 3, вписана в параллелограмм, а вторая касается двух сторон параллелограмма и первой окружности. Расстояние между точками касания, лежащими на одной стороне параллелограмма, равно 3. Найдите площадь параллелограмма.

Задача по математике — 4169

Дана окружность радиуса 1. Из внешней точки $M$ к ней проведены две взаимно перпендикулярные касательные $MA$ и $MB$. Между точками касания $A$ и $B$ на меньшей дуге $AB$ взята произвольная точка $C$ и через неё проведена третья касательная $KL$, образующая с касательными $MA$ и $MB$ треугольник $KLM$. Найдите периметр этого треугольника.

Задача по математике — 4170

Две окружности радиусов $R$ и $r$ касаются сторон данного угла и друг друга. Найдите радиус третьей окружности, касающейся сторон того же угла, и центр которой находится в точке касания двух данных окружностей между собой.

Задача по математике — 4171

В треугольник со сторонами 6, 10, и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника.

Задача по математике — 4172

Сторона треугольника равна 48, а высота, проведённая к этой стороне, равна 8,5. Найдите расстояние от центра окружности, вписанной в этот треугольник, до вершины, противоположной данной стороне, если радиус вписанной окружности равен 4.

Задача по математике — 4173

В угол вписаны три окружности — малая, средняя и большая. Большая окружность проходит через центр средней, а средняя — через центр малой. Вычислите радиусы средней и большой окружности, если радиус малой равен $r$, и расстояние от её центра до вершины угла равно $a$.

Задача по математике — 4174

Три окружности радиусов 1, 2 и 3 касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей.

Задача по математике — 4175

В равносторонний треугольник со стороной $a$ вписана окружность. К окружности проведена касательная так, что её отрезок внутри треугольника равен $b$. Найдите площадь треугольника, отсечённого этой касательной.

Задача по математике — 4176

Три окружности разных радиусов попарно касаются друг друга внешним образом. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы большей и средней равны 6 и 4.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

В параллелограмме лежат две окружности одна из них радиуса 3

В параллелограмме ABCD расположены две равные непересекающиеся окружности. Первая касается сторон AD, AB и BC, вторая — сторон AD, CD и BC.

а) Докажите, что общая внутренняя касательная l окружностей проходит через точку пересечения диагоналей параллелограмма ABCD.

б) Пусть ABCD — прямоугольник, а прямая l касается окружностей в точках M и N. Найдите площадь четырёхугольника с вершинами в точках M, N и в центрах окружностей, если AD = 36 , а расстояние между центрами окружностей равно 20.

а) Пусть O — точка пересечения диагонали AC параллелограмма с общей внутренней касательной l к данным окружностям, P и Q — точки пересечения прямой l со сторонами AD и BC соответственно. Достаточно доказать, что O — середина диагонали AC.

Пусть O₁ и O₂ — центры первой и второй окружностей соответственно. Первая окружность касается стороны AD в точке K, вторая окружность касается стороны BC в точке L.

Лучи AO₁ и CO₂ — биссектрисы равных углов BAD и BCD, значит, прямоугольные треугольники AKO₁ и CLO₂ равны по катету (радиусы равных окружностей) и противолежащему острому углу. Тогда AK = CL. Аналогично KP = LQ. Следовательно,

Значит, треугольники AOP и COQ равны по стороне и двум прилежащим к ней углам, поэтому AO = OC, а точка O — середина диагонали AC, то есть центр параллелограмма ABCD.

б) Поскольку ABCD — прямоугольник, его сторона AD равна сумме диаметра окружности и отрезка O₁O₂, то есть 2r + O₁O₂ = AD, 2r + 20 = 36, следовательно, r = 8.

Четырёхугольник O₁MO₂N — параллелограмм, так как его противоположные стороны O₁M и O₂N равны и параллельны. Диагонали O₁O₂ и MN параллелограмма O₁MO₂N пересекаются в точке O и делятся этой точкой пополам.

Площадь параллелограмма O₁MO₂N в четыре раза больше площади треугольника OO₁M, в котором По теореме Пифагора

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Геометрия Две окружности имеют общий центр O (см. рис.). В одной из окружностей проведен диаметр ABСкачать Задание №20 ОГЭ по математике Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать Анализ геометрических высказываний В 20 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные. Это задание не имеет какого либо подхода к решению, однако ниже я привел несколько разобранных задач. Разбор типовых вариантов задания №20 ОГЭ по математике Первый вариант задания Какие из следующих утверждений верны? Все диаметры окружности равны между собой. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. Любые два равносторонних треугольника подобны. Решение: Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны. Второй вариант задания Какие из следующих утверждений верны? Все высоты равностороннего треугольники равны. Существуют три прямые, которые проходят через одну точку. Если диагонали параллелограмма равны, то он является ромбом. Решение: Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат. Третий вариант задания Какие из следующих утверждений верны? Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. Любой прямоугольник можно вписать в окружность. Через заданную точку плоскости можно провести единственную прямую. Решение: Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку. Демонстрационный вариант ОГЭ 2019 Укажите номера верных утверждений. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. Треугольник со сторонами 1, 2, 4 существует. Если в ромбе один из углов равен 90° , то такой ромб — квадрат. В любом параллелограмме диагонали равны. Решение: Проанализируем каждое из утверждений: 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. Да, такое утверждение в геометрии есть, с дополнением » и только одну» : «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.» 2) Треугольник со сторонами 1, 2, 4 существует. Для существования треугольника должно выполняться следующее правило: Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2 Четвертый вариант задания Какое из следующих утверждений верно? 1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом. 2) Смежные углы всегда равны. 3) Каждая из биссектрис равнобедренного треугольника является его высотой. Решение: Проанализируем каждое утверждение. 1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата. 2) Это утверждение неверно. Основание – соответствующая теорема, которой утверждается, что смежные углы в сумме имеют 180 0 , т.е. дополняют друг друга до развернутого угла. Следовательно, равенство смежных углов может иметь место только в случае, если достоверно известно, что один из них прямой. 3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника. Пятый вариант задания Какое из следующих утверждений верно? 1) Если угол острый, то смежный с ним угол также является острым. 2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом. 3) Касательная к окружности параллельна радиусу, проведённому в точку касания. Решение: Выполняем анализ утверждений. 1) Согласно теореме о смежных углах, их сумма всегда равна 180 0 . Это означает, что любой из смежных углов является разностью 180 0 и величины 2-го смежного угла. Если первый смежный угол острый, значит, второй равен разности 180 0 и острого угла (т.е. угла, меньшего 90 0 ), которая в любом случае окажется больше 90 0 . А угол, больший 90 0 , по определению тупой. Итак, утверждение неверно. 2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно. 3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно. 🎬 Видео Параллельные прямые | Математика | TutorOnlineСкачать №9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости αСкачать На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.Скачать Стереометрия 10 класс. Часть 1 | МатематикаСкачать Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать Окружность и круг, 6 классСкачать 8 класс, 4 урок, ПараллелограммСкачать Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать Планиметрия 29 | mathus.ru | Окружность, касающаяся биссектрисы и двух сторон параллелограммаСкачать 8 класс, 13 урок, Площадь параллелограммаСкачать Две окружности касаются внешним образом. ЕГЭ Задача 16Скачать Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать ОГЭ Задание 26 Внешнее касание двух окружностейСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности