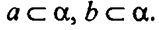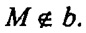В параллельно вс прямая а не принадлежит плоскости авс доказать

Здарово. Поможете решить?

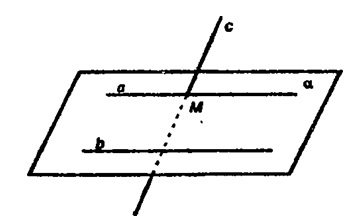
Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а. Докажите, что b и с — скрещивающиеся прямые.

Могу помочь, если актуально еще

Т.к. а || b, то существует пл. α, что
Пусть с пересекает а в т. М. а || b, значит,
По признаку скрещивающихся прямых, с и b скрещиваются.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Прямая МК, не лежащая в плоскости АВС, параллельна стороне АВ, параллелограмма АВСD?

Геометрия | 5 — 9 классы

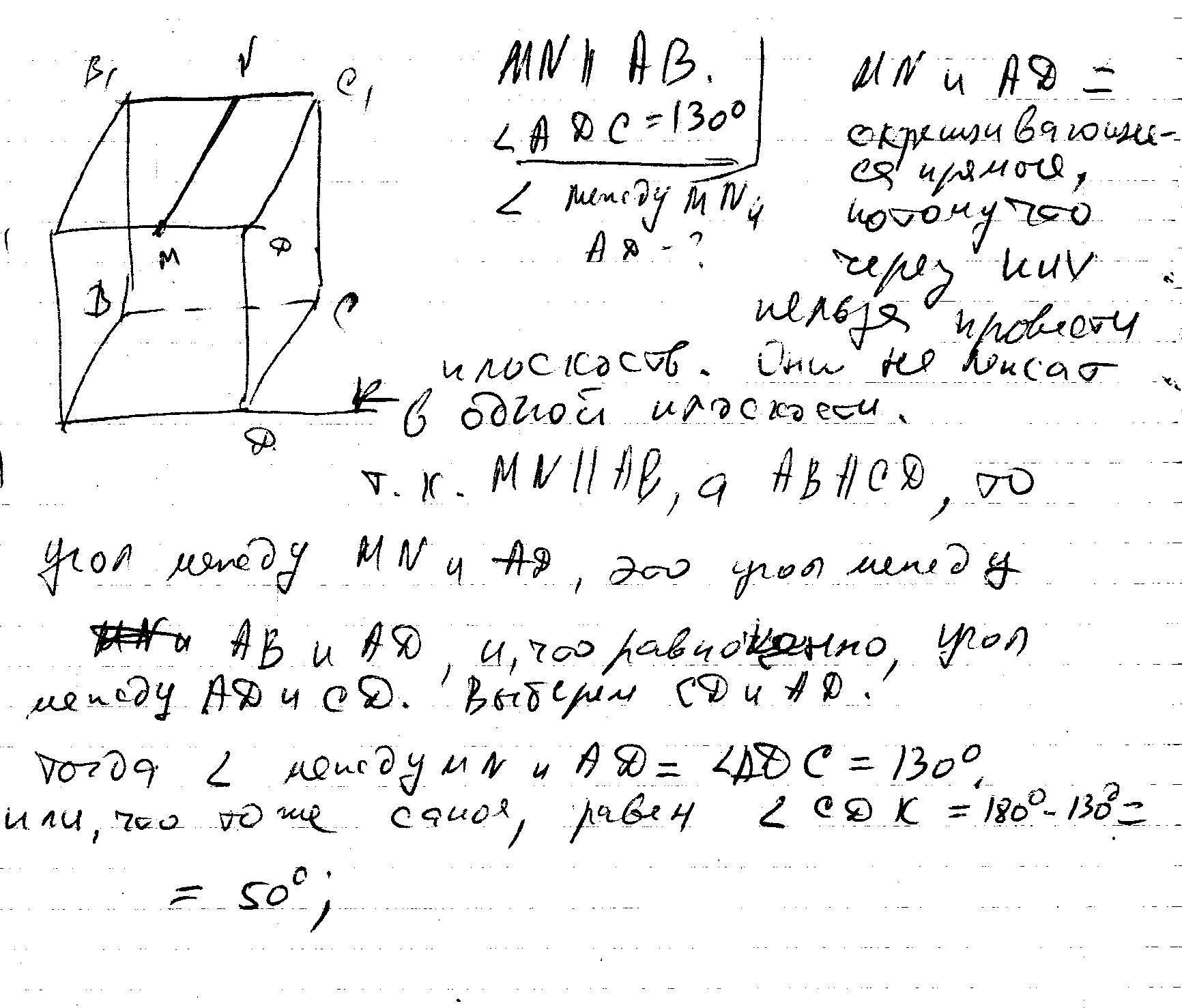
Прямая МК, не лежащая в плоскости АВС, параллельна стороне АВ, параллелограмма АВСD.

Выясните, взаимное расположение прямых МК и АD?

И найдите угол между ними, если угол АDС = 130градусов.

Пжл с решением очень прошу!

Решение в скане.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Прямая mk не лежит пл — ти ab, параллельна стороне ab параллелограмма abcd?

Прямая mk не лежит пл — ти ab, параллельна стороне ab параллелограмма abcd.

Выяснить взаимное расположение прямых mk и ad и найти угол между ними, если угол adc = 130градусов.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Прямая KM параллельна BC параллелограмма ABCD и не принадлежит его плоскости ?

Прямая KM параллельна BC параллелограмма ABCD и не принадлежит его плоскости .

Выясните взаимное расположение прямых KM и AB и найдите угол между ними если угол ABC равен 110 градусов.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

1. В треугольнике АВС угол В = 40 градусов?

1. В треугольнике АВС угол В = 40 градусов.

Через вершину С проведена прямая, которая параллельна стороне АВ и образует с АС угол 40 градусов.

Найдите углы А и С в треугольнике АВС.

2. Дан угол АВС, равный 68 градусам.

Через точку D, лежащую на его биссектрисе, проведена прямая, параллельная прямой ВС и пересекающая сторону АВ в точке Е.

Найдите все углы треугольника ВDЕ.

Видео:10 класс, 2 урок, Аксиомы стереометрииСкачать

Прямая m параллельно диагонали МР ромба MNРК и не лежит в плоскости ромба, каково взаимное расположение прямых m и NP?

Прямая m параллельно диагонали МР ромба MNРК и не лежит в плоскости ромба, каково взаимное расположение прямых m и NP?

Найдите угол между ними, угол MNP = 60 градусов угол NPK = 110 градусов(Полное решение прошу).

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямая KM параллельна стороне BC параллелограмма ABCD и не лежит в плоскости ABC?

Прямая KM параллельна стороне BC параллелограмма ABCD и не лежит в плоскости ABC.

Выясните взаимное расположение прямых KM и AB и найдите угол между ними если угол ABC = 110градусов.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Точки М, К и прямая АВ не лежат в одной плоскости?

Точки М, К и прямая АВ не лежат в одной плоскости.

Каково взаимное расположение прямых МК и АВ.

Видео:№24. Точка М не лежит в плоскости трапеции ABCD с основанием AD.Скачать

Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону Р — середина стороны AD точка К середина стороны CD Каково взаимное расположение прямых РК и АВ ?

Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону Р — середина стороны AD точка К середина стороны CD Каково взаимное расположение прямых РК и АВ ?

Чему равен угол между прямыми РК И АВ если АВС = 40 градусов и ВСА = 80 градусов.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Через вершину прямого угла С треугольника АВС проведена прямая СD параллельная стороне АВ?

Через вершину прямого угла С треугольника АВС проведена прямая СD параллельная стороне АВ.

Найти угол А и В, если угол DСВ = 37 градусов.

Видео:Стереометрия - это ПРОСТО! Урок 1. Аксиомы Теоремы Задачи. Геометрия 10 классСкачать

1. Середины сторон CD и АВ параллелограм­ма ABCD лежат в плоскости , а сторона ВС не лежит в этой плоскости?

1. Середины сторон CD и АВ параллелограм­ма ABCD лежат в плоскости , а сторона ВС не лежит в этой плоскости.

Докажите, что прямая AD и плоскость параллельны.

2. Точки А, В, С и D не лежат в одной плоскости.

Докажите, что любые три из них являются вершинами треугольника 3.

Прямая КМ параллельна стороне ВС треугольника AВС и не лежит в плоскости АВС.

Выясните взаимное расположение прямых КМ и АВ и найдите угол между ними, если АВС = 105°.

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Помогите очень прошу?

Помогите очень прошу.

В треугольнике АВС угол А равен 50 градусам, угол С равен 80 градусам.

Докажите, что биссектриса внешнего угла треугольника при вершине С лежит на прямой, параллельной прямой АВ.

На этой странице находится вопрос Прямая МК, не лежащая в плоскости АВС, параллельна стороне АВ, параллелограмма АВСD?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Средняя линия треугольника соединяет середины двух сторон и равна половине третьей стороны, таким образом : DF — средняя линия ΔAOC и AC = 2DF. DE — средняя линия ΔAOB и AB = 2DE. EF — средняя линия ΔBOC и BC = 2EF. ΔABC

ΔDFE по трём сторонам (они..

Осевое сечение цилиндра — квадрат т. Е 2R = 5 R = 2. 5 H = 5 S(полн) = 2πR² + 2πRH = 12. 5π + 25π = 37. 5π.

3400мм + 24мм + 1600мм + 93мм = 5117мм = 51 дм 17мм.

Вот если пригодиться).

Решение смотри на фото.

1)14х2 = 28 см(катет, лежащий напротив угла в 30 градусов равен половине гипотенузы).

28 так как сторона AC лежит напротив угла B = 30 град.

Если внешний 130, внутренний у основания будет 180 — 130 = 50 (смежные углы) значит второй у основания тоже 50, тк равнобедренный треугольник. Угол при вершине будет 180 — 50 — 50 = 80 (сумма всех углов любого треугольника 180) Ответ : 80 ; 50 ; 50.

🎥 Видео

Параллельность прямой к плоскостиСкачать

Геометрия 10 класс (Урок№8 - Перпендикулярность прямой и плоскости.)Скачать

10 класс, 10 урок, Параллельные плоскостиСкачать

№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

Параллельность прямых. 10 класс.Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать