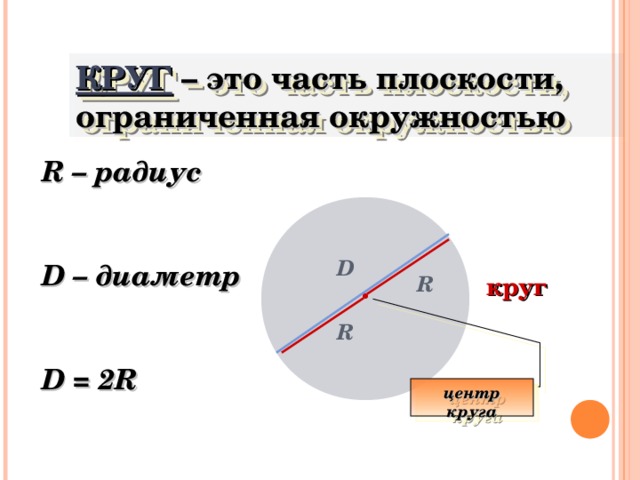
На срубе дерева который имеет форму окружности в центре (2 видео)

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

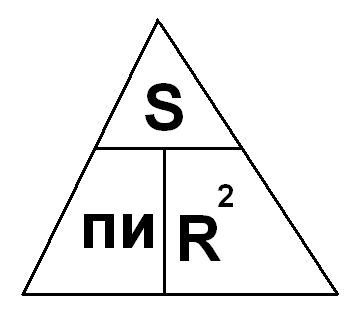
Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Содержание

Открытый урок математики на тему «Круг»
Просмотр содержимого документа «План»
Просмотр содержимого презентации «К Р У Г»
Пробный экзаменационный вариант «ОГЭ математика пробник 138 вариант» (2022)
🔥 Видео

Видео:Снятие коры с брёвен для рубленных домов.Скачать

Открытый урок математики на тему «Круг»

Просмотр содержимого документа
«План»

План — конспект отрытого урока для учащихся 6а класса:

«Круг. Площадь круга».

Подготовила и провела учитель математики

высшей категории МБОУ Краснинской СОШ

1). Повторить знания учащихся о круге; 2). показать отличия круга от прочих геометрических фигур, в первую очередь, от окружности; 3). повторить понятие о площади круга; 4). опытным путем вывести формулу для вычисления площади круга и ее производные формулы.

1). учить осознанно различать круг и окружность; 2). формировать умение находить площадь круга по формуле и величины, производные из данной формулы; 3). формировать умение решать задачи с элементами курса геометрии; 4). закреплять и повторять ранее пройденный материал.

1). развивать у уч-ся умение работать в группе и индивидуально; 2). показать место круга и окружности в окружающем мире; 3). прививать интерес к математике и математическим наукам; 4). развивать культуру вычисления; 5). дополнять знания уч-ся историческими фактами о математике; 6). развивать память, логическое и пространственное мышление, эрудицию, математически и литературно грамотную речь (устную и письменную).

1). развивать усидчивость, самостоятельность, самоконтроль, наблюдательность; 2). воспитывать аккуратность, дисциплинированность, желание и умение помогать товарищам.

1). Учебники, тетради, чертежные принадлежности; 2). плотный цветной картон, клей; (или оборудование для магнитной доски) 3). ножницы, нить; 4). демонстрационные чертежные принадлежности для работы у доски; 5). портреты ученых; 6). карточки с индивидуальными заданиями; 7). компьютер на платформе IBM PC ; 8). демонстрационный проектор, экран; 9). диск с скомпонованным ПО (презентационный материал Power Point и др.); 10). предметы бытового обихода для демонстрации окружности (банка для кофе, циферблат часов, кружка и т.д.); 11). материал для демонстрации окружностей (конус, окружность из картона и т.д.).

(Разбор затруднений, возникших в процессе выполнения домашнего задания. Ряд вопросов на проверку осознанности выполнения домашнего задания.)

(Устный счет, на основе презентационного материала на экране компьютера) Индивидуальная и групповая работа, если учащийся затрудняется в выборе правильного ответа.

ЭТАП ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА

СЛАЙД 2-4 (Презентация «КРУГИ»)

1). (Краткий опрос на повторение ранее изученного теоретического материала: что такое окружность, радиус, диаметр, центр окружности, длина окружности, формула для вычисления длины окружности.)

(Также учащимся раздаются карточки для проведения устного математического диктанта. Ответы диктанта высвечиваются на доске – экранной копии карточки.)

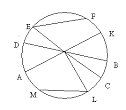
Какая геометрическая фигура изображена на чертеже?

Назовите центр окружности.

Чем является отрезок АК?

Есть ли на чертеже еще диаметры?

Чем является отрезок ОВ?

Есть ли на чертеже еще радиусы?

С помощью какого измерительного прибора это можно сделать? Какими единицами измерения будет выражен результат?

Можно ли измерить длину окружности? С помощью какого измерительного прибора это можно сделать? Как это можно сделать? (Возможные ответы: с помощью нитки, веревки и т.п.)

Расстояние от центра окружности до её любой точки называется.

Площадь прямоугольника вычисляется по формуле….(S=ab).

По формуле 2πR вычисляется…

Как называется число, приближенно равное 3,14.

Что вычисляют по формуле 2** R…

Сколько пройдет времени, если минутная стрелка сделает полный круг? (возможна демонстрация на циферблате)

2). Задачи на повторение (по вариантам) СЛАЙД 5 (Презентация «КРУГИ»).

3). Перед учащимися ставится проблемная задача (СЛАЙДЫ 6 (Презентация «КРУГ»)

Директору цирка потребовалось выяснить, сколько обивочного материала нужно заказать, чтобы целиком обтянуть арену для выступлений, радиус которой соответствует международным стандартам и равен 40,8 м.

Можем ли мы сейчас ответить на вопрос задачи, чтобы помочь директору?

Как вы думаете, что необходимо знать, чтобы решить данную задачу?

4). Постановка цели и задач урока.

Понятие круга как части плоскости, ограниченной окружностью.

Здесь и далее – учащимся выдаются карточки с «мнемическими» стихотворениями для лучшего запоминания

Знакома всем ее наружность.

Она идет по краю круга

Введение понятия площади круга, центра, радиуса и диаметра круга.

Историческая справка «О круглых телах».

Для первобытных людей важную роль играла форма окружающих их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек деревья и деревья, которые годятся лишь на дрова, вкусные орехи от горьких или ядовитых. Особенно вкусны орехи кокосовой пальмы. Эти орехи очень похожи на шар.

А добывая каменную соль или горный кварц, люди наталкивались на кристаллы, потом научились шлифовать их. Отшлифованные орудия позволили быстро срубить дерево, разрезать мясо, помогали лучше охотиться на зверей. Специальных названий для геометрических фигур тогда не было. Говорили: “Такой, как кокосовый орех”, (т. е. круглый), “такой, как соль” (т. е. имеющий форму куба). Некоторые формы фигур казались особо красивыми. И действительно, нельзя без восхищения смотреть на красоту кристаллов, цветов, фигур, имеющих правильную круглую форму.

Только в Древней Греции окружность и круг получили свои названия.

Круглые тела в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.

В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!

Круг – колесо – прогресс (движение вперед)

Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.

Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.

Колесо — одно из великих изобретений, которое было сделано в IV тысячелетии до н.э. на Древнем Востоке. Итак, для чего же мы вспомнили про колесо? Оказывается, что в переводе опять же с латинского слово «радиус» переводится не иначе как «спица колеса».

Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму.

Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность.

Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания. Самым важным среди круглых тел был шар.

2). Выведение формулы для нахождения площади круга

Предварительная домашняя заготовка каждого ученика

На листе цветной бумаги начертить окружность с произвольным радиусом и провести фломастером по её контуру.

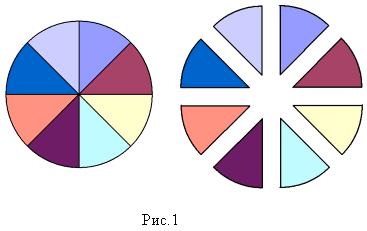
Разделить круг с помощью линейки и карандаша на несколько секторов, затем разрезать его. Заметим, что не следует делить круг на меньшее, чем 8 секторов.

В одном из секторов следует провести радиус, делящий его на 2 равных сектора, которые назовём крайними, и отложить.

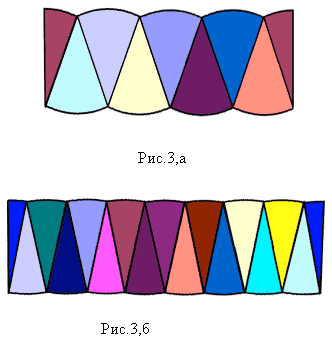
На картонном листе провести горизонтальную прямую и приклеить вдоль неё сектора, как показано на рис. (На рис. а – круг разделен на 8 секторов, на рис. б – на 16 секторов). Крайние сектора приклеить по краям.

Посмотрим и покажем друг другу свою домашнюю заготовку к этому уроку.

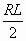
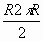
Заметно, что получившаяся фигура при увеличении количества секторов становится очень похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади прямоугольника. Ширина нашего прямоугольника равна радиусу окружности(R), а длина прямоугольника равна половине длины окружности ( L /2). Площадь прямоугольника равна произведению длины на ширину, т. е. S= , а т.к. L=2πR, значит S= или S=πR 2 .

Значит, площадь круга равна: S=πR 2 .

СЛАЙД 14 (Презентация «КРУГ»

Запись уч-ся формулы в тетради.

Выведение производных формул:

СЛАЙД 15 (Презентация «КРУГ»

(Выяснение с учащимися, чем отличается окружность от круга, и чем похожи эти фигуры.)

3). Решение задачи, предложенной выше в качестве проблемной.

ЭТАП ПРИМЕНЕНИЯ ПОЛУЧЕННЫХ ЗНАНИЙ НА ПРАКТИКЕ

Задания в карточках

(Задачи также появляются на презентационном экране – Презентация «Задачи»)

(Учащиеся вынимают из конверта круги различного диаметра.) Выполнить необходимые измерения и вычислить площадь круга и длину его окружности.

ЭТАП ЗАКРЕПЛЕНИЯ ПРОЙДЕННОГО МАТЕРИАЛА

VII . Решение задач на закрепление ранее пройденного материала

(при наличии свободного времени на уроке)

Задание №3 (под диктовку или в карточках)

Задача про корову:

СЛАЙДЫ 1-2 (Презентация «КРУГ 2»

VII . Подведение итогов урока. Домашнее задание

1). Итоговое тестирование по новому материалу

(Используется тестирование на основе ПО MS Power Point – работа и обсуждение в парах)

2). Вопросы на закрепление и анализ тестирования:

Назовите предметы или явления окружающего мира, где можно столкнуться с окружностью.

Чем круг отличается от окружности?

Запишите формулу для вычисления площади круга.

В чем может измеряться площадь круга?

3). Разбор домашней задачи (в карточках):

Задача про Останкинскую телебашню

(При решении данной задачи в случае затруднения понимания смысла вопроса можно использовать наглядную демонстрацию слайда СЛАЙДЫ 18-20 (Презентация «КРУГ» ) Здесь же — краткая энциклопедическая информация о башне.

4). Оценивание работы уч-ся на уроке

Знать формулу для вычисления площади круга;

№1-2 (раздаточный материал — карточки);

Решить кроссворд (в карточках)

Презентация прилагается на флешке

Просмотр содержимого презентации
«К Р У Г»

К Р У Г ПЛОЩАДЬ КРУГА

Составитель: Серова Н.Н.

Какая геометрическая фигура изображена на чертеже?
Назовите центр окружности
Чем является отрезок АК?
Есть ли на чертеже еще диаметры?
Чем является отрезок ОВ?
Есть ли на чертеже еще радиусы?

С помощью какого измерительного прибора можно измерить радиус? В каких единицах измерения может быть выражен результат?
Можно ли ИЗМЕРИТЬ длину окружности? Как это можно сделать?
Расстояние от центра окружности до любой ее точки называется…
Площадь ПРЯМОУГОЛЬНИКА вычисляется по формуле…

По формуле 2πR вычисляется…
Как называется число, приближенно равное 3,14?
Сколько пройдет времени, если минутная стрелка сделает полный круг? Путь, который при этом проделает точка на конце стрелки, будет равен… (какой величине?)
Чем будет являться минутная стрелка в данном случае?

КРУГ – это часть плоскости, ограниченная окружностью

Видео:Сруб или капитальный дом? Выбор стоил мне очень дорого.Скачать

Пробный экзаменационный вариант «ОГЭ математика пробник 138 вариант» (2022)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

1. Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. В ответ запишите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.

На рисунке изображён план сельской местности.

Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.

Шоссе и просёлочные дороги образуют прямоугольные треугольники.

По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.

2. Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.

3. Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.

4. Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?

5. На просёлочных дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино, как и на путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

6. Вычислите:

7. Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?

8. Найдите значение выражения если

9. Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

10. На экзамене 25 билетов, Костя не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.

11. Установите соответствие между графиками функций и формулами, которые их задают.

В таблице под каждой буквой укажите соответствующий номер.

12. Закон Кулона можно записать в виде где — сила взаимодействия зарядов (в ньютонах), и — величины зарядов (в кулонах), — коэффициент пропорциональности (в Н·м 2 /Кл 2 ), а — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда (в кулонах), если Н·м 2 /Кл 2 , Кл, м, а Н.

13. Решите систему неравенств

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

3) система не имеет решений

14. Улитка ползет вверх по дереву, начиная от его основания. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За сколько минут улитка достигнет вершины дерева высотой 5,25 м? В ответе укажите число минут.

15.

ABCDEFGHI — правильный девятиугольник. Найдите угол DAC. Ответ дайте в градусах.

16.

Отрезок AB = 9 касается окружности радиуса 12 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

17. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какое из следующих утверждений верно?

1. Все прямоугольные треугольники подобны.

2. Через заданную точку плоскости можно провести только одну прямую.

3. Диагонали ромба точкой пересечения делятся пополам.

В ответ запишите номер выбранного утверждения.

20. Сократите дробь:

21. Свежие фрукты содержат 78 % воды, а высушенные — 22 %. Сколько требуется свежих фруктов для приготовления 22 кг высушенных фруктов?

22. Постройте график функции

и определите, при каких значениях прямая имеет с графиком ровно две общие точки.

23. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

24. В остроугольном треугольнике ABC угол B равен 60° . Докажите, что точки A, C, центр описанной окружности треугольника ABC и центр вписанной окружности треугольника ABC лежат на одной окружности.

25. На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 15, MD = 12, H — точка пересечения высот треугольника ABC. Найдите AH.

На рисунке изображён план сельской местности.

Шоссе и просёлочные дороги образуют прямоугольные треугольники.

Пользуясь описанием и рисунком, можно заметить, что деревня Егорка соответствует цифре 2, деревня Доломино — цифре 3, деревня Ванютино — цифре 4, деревня Жилино — цифре 5, деревня Горюново — цифре 6, деревня Богданово — цифре 7.

2. Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.

Расстояние от Антоновки до Доломино состоит из расстояний от Антоновки до Егорки и от Егорки до Доломино, следовательно, расстояние от Антоновки до Егорки равно км.

3. Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.

Расстояние от Егорки до Жилино соответствует гипотенузе прямоугольного треугольника с катетами 12 км и 9 км. По теореме Пифагора (км.)

Расстояние от Антоновки до Горюнова соответствует гипотенузе треугольника с катетами 20 км и 15 км. Найдем ее по теореме Пифагора: км. По проселочной дороге Таня с дедушкой едут со скоростью 30 км/ч. Следовательно, на путь от Антоновки до Горюново они затратят часа или 50 минут. Расстояние от Горюново до Богданово 6 км, скорость по шоссе Тани с дедушкой составляет 50 км/ч. Следовательно, на путь от Горюново до Богданово они затратят часа или 7,2 минуты. Таким образом, на весь путь Таня с дедушкой затратят минуты.

Пусть x литов — расход бензина по шоссе на 100 км. Путь из Антоновки до Богданово через Ванютино проходит полностью по шоссе. Расстояние является суммой расстояний от Антоновки до Ванютино и от Ванютино до Богданово, то есть Следовательно, бензина будет затрачено литров.

Длина пути из Антоновки до Богданово через Доломино и Горюново равна сумме расстояний от Антоновки до Доломино и от Горюново до Богданова пройденных по шоссе, и расстояния от Доломина до Горюнова по проселочной дороге. Следовательно, бензина будет затрачено литров.