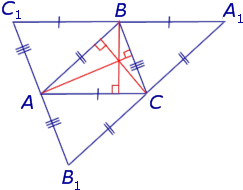
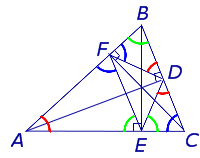
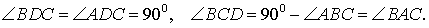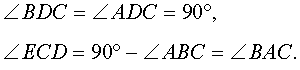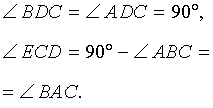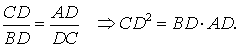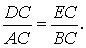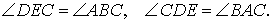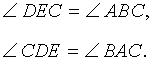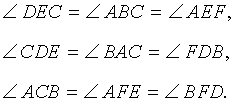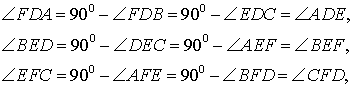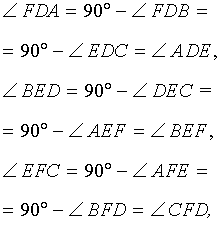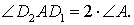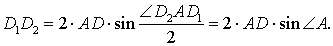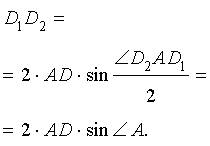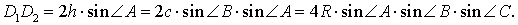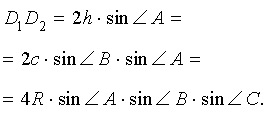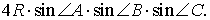В любом треугольнике все три высоты пересекаются в одной точке. Все высоты в остроугольном треугольнике лежат внутри треугольника (как и точка пересечения высот).
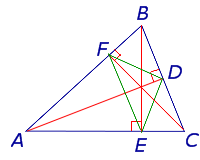
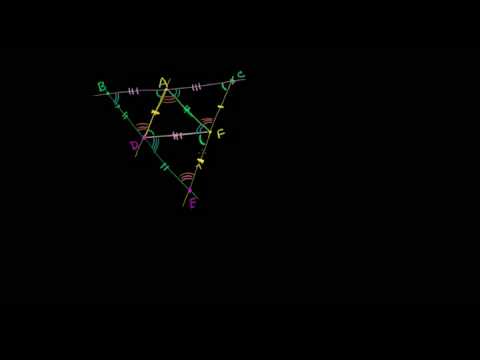
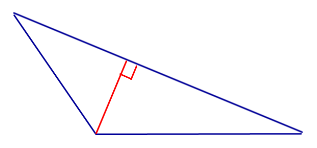
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Доказать, что углы BB1C1 и BCC1 равны; углы B1C1С и BB1C равны.
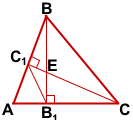
Около любого треугольника можно описать окружность. Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. Радиус такой окружности равен половине гипотенузы.
Центр описанной около прямоугольного треугольника BCC1 окружности — середина гипотенузы BC, радиус равен половине BC.
Значит эти треугольники вписаны в одну и ту же окружность.
Следовательно, точки B, C, B1 и C1лежат на одной окружности.
∠B1C1С=∠B1BC (как вписанные углы, опирающиеся на одну дугу B1C).
Что и требовалось доказать.
То есть решение такого рода задач начинаем с поиска прямоугольных треугольников с общей гипотенузой.
- 2 Comments
- Свойства высот треугольника. Ортоцентр
- Высота треугольника. Задача Фаньяно
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
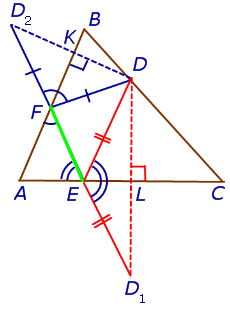
- Задача Фаньяно
- 💡 Видео
Видео:Точка пересечения высот треугольника.Скачать

2 Comments
Здравствуйте!
во втором случае: Угол ВВ1С — прямой, имелся в виду угол В1ВС, как опирающийся на дугу В1С
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Свойства высот треугольника. Ортоцентр
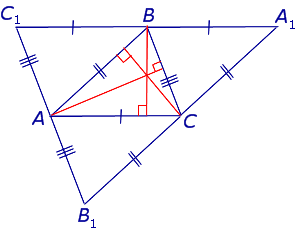
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если 

- Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
- Четырехугольник ВКМН также можно вписать в окружность.
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
- ,где R – радиус описанной окружности .
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.
2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .
Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.
3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.
5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .
Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .
— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
Видео:Геометрия 7.Треугольники урок 6. Высота треугольника. Определение, свойства, точки пересечения высотСкачать

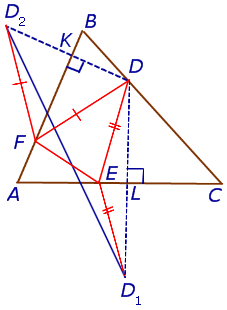
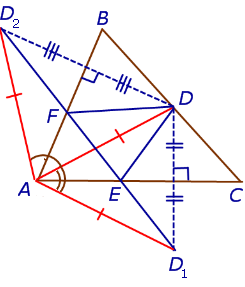
Высота треугольника. Задача Фаньяно
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Высота треугольника. Свойство высоты прямоугольного треугольника
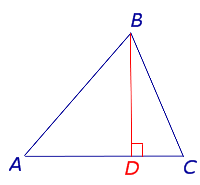
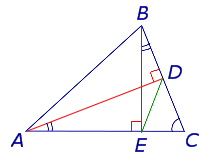
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
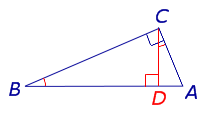
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
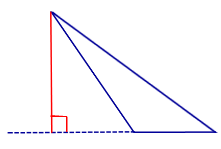
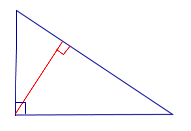
| Остроугольный треугольник |  | Все высоты остроугольного треугольника лежат внутри треугольника. |
 | ||
 | ||
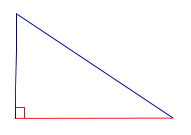
| Прямоугольный треугольник |  | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
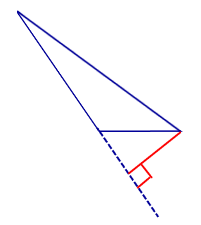
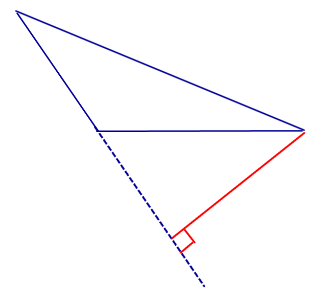
| Тупоугольный треугольник | 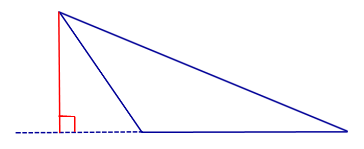 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Геометрия Высоты остроугольного треугольника ABC пересекаются в точке H Докажите что радиусыСкачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
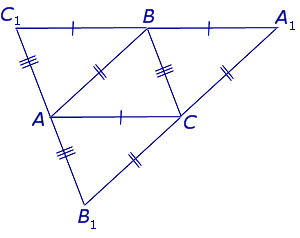
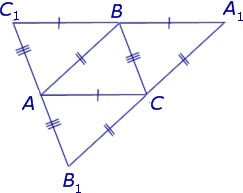
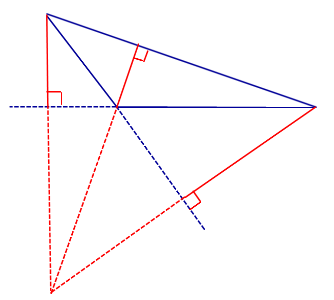
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:Высоты треугольника.Скачать

Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 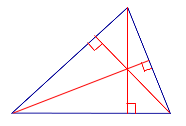 | |
| Прямоугольный треугольник | 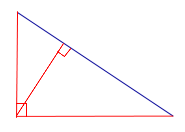 |