В остроугольном треугольнике абс точки а с центр описанной окружности

В остроугольном треугольнике ABC точки A, C, центр описанной окружности O и центр вписанной окружности I лежат на одной окружности. Докажите, что угол ABC равен 60°.

Точка I — центр вписанной окружности, то есть точка пересечения биссектрис треугольника АВС. Углы IAC и ICA равны половинам углов А и С треугольника АВС.
Тогда

Точка О – центр описанной окружности треугольника АВС. Значит, угол АВС – вписанный в эту окружность,

Поскольку точки А, О, I, С лежат на одной окружности, углы АОС и АIС равны.
Тогда и

Видео:Геометрия В треугольнике ABC точка O – центр описанной окружности, точка L – середина стороны ABСкачать

В остроугольном треугольнике АВС точки А, С, центр описанной окружности О и точка пересечения высот Н лежат на одной окружности?

Геометрия | 5 — 9 классы

В остроугольном треугольнике АВС точки А, С, центр описанной окружности О и точка пересечения высот Н лежат на одной окружности.

Докажите что угол АВС равен 60.

Условие, что O и H лежат на одной окружности с точками A и С, означает, что в этой окружности углы AOB и AHС — вписанные, опирающиеся на одну и ту же дугу.

То есть они равны.

Дальше все проще простого.

∠AOС = 2 * ∠ABC (это связь между центральным и вписанным углами, на этот раз — в окружности, описанной вокруг ABC).

∠HAC = 90° — ∠BCA ; ∠HCA = 90° — ∠BAC ; = &gt ; ∠AHC = 180° — (90° — ∠BCA) — (90° — ∠BAC) = ∠BAC + ∠BCA = 180° — ∠ABC ;

То есть 2 * ∠ABC = 180° — ∠ABC ;

Видео:Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

Точки А, В и С лежат на окружности с центром О?

Точки А, В и С лежат на окружности с центром О.

Найдите угол АОС, если Угол АВС = 66 градусов.

Видео:Геометрия В остроугольном треугольнике ABC точки A, C, точка пересечения высот H и центр вписаннойСкачать

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот ?

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот .

2)центром вписанной окружности треугольника является точка пересечения его медиан.

3) центром вписанной окружности является точка пересечения его биссектрис .

4)центром описанной окружности треугольника является точка пересечения его высот.

5) центром описанной окружности треугольника является точка пересечения его медиан .

6) центром описанной окружности треугольника является точка пересечения его биссектрис.

Видео:Задание 25 Вписанная и описанная окружностиСкачать

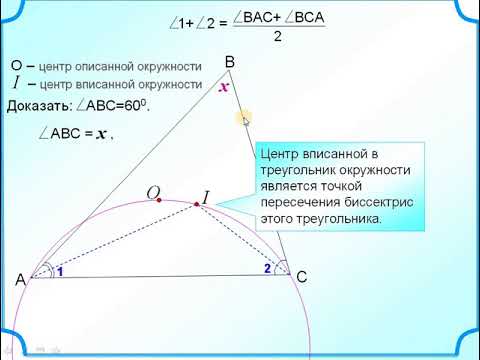
В остроугольном треугольнике abc точки а, с, центр описанной окружности O ицентр вписанной окружности I лежат на одной окружности?

В остроугольном треугольнике abc точки а, с, центр описанной окружности O ицентр вписанной окружности I лежат на одной окружности.

Докажите что угол авс равен 60 градусов.

Видео:Построить описанную окружность (Задача 1)Скачать

Доказать, что середины сторон треугольника, основания высот и середины отрезков, соединяющих точку Н пересечения высот с вершинами треугольника, лежат на одной окружности, причем центр Р круга с серед?

Доказать, что середины сторон треугольника, основания высот и середины отрезков, соединяющих точку Н пересечения высот с вершинами треугольника, лежат на одной окружности, причем центр Р круга с серединой ОН, где О — центр окружности, описанной вокруг заданного треугольника АВС.

Видео:ОГЭ 2021 Задание 24Скачать

В треугольнике АВС проведена высота АН ; О — центр описанной окружности?

В треугольнике АВС проведена высота АН ; О — центр описанной окружности.

Докажите, что угол ОАН равен модулю разности уголов В и С.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Высоты остроугольного треугольника ABС, проведенные из точек В и С, продолжили до пересечения с описанной окружностью в точках В1 и С1?

Высоты остроугольного треугольника ABС, проведенные из точек В и С, продолжили до пересечения с описанной окружностью в точках В1 и С1.

Оказалось, что отрезок В1С1, проходит через центр описанной окружности.

Найдите угол ВАС.

Видео:Точка O центр окружности описанной около остроугольного треугольникаСкачать

Точки А, В и С лежат на окружности с центром в точке О?

Точки А, В и С лежат на окружности с центром в точке О.

Лежит ли центр окружности на отрезке АС, если : ∠АВС = 210градусов.

Видео:Задание 16 ЕГЭ по математикеСкачать

Докажите что радиус окружности описанной вокруг остроугольного треугольника равен радиусу окружности, проходящей через точку пересечения её высот и две вершины треугольника?

Докажите что радиус окружности описанной вокруг остроугольного треугольника равен радиусу окружности, проходящей через точку пересечения её высот и две вершины треугольника.

Видео:Геометрия В остроугольном треугольнике ABC проведены высоты AP и CQ. а) Докажите, что угол PACСкачать

Треугольник авс вписан в окружность с центром в точке о?

Треугольник авс вписан в окружность с центром в точке о.

Точка о и с лежат в одной полуплоскости относительно прямой ав.

Найдите угол асв, если угол аов равен 67 градусов.

Видео:Радиус описанной окружностиСкачать

Точка М, не лежащая в плоскости треугольника АВС, равноудалена от его сторон?

Точка М, не лежащая в плоскости треугольника АВС, равноудалена от его сторон.

МО – перпендикуляр к плоскости АВС.

Тогда точка О является 1 — центром тяжести треугольника АВС 2 — точкой пересечения высот треугольника АВС 3 — центром вписанной в треугольник АВС окружности 4 — центром описанной около треугольника АВС окружности.

Вопрос В остроугольном треугольнике АВС точки А, С, центр описанной окружности О и точка пересечения высот Н лежат на одной окружности?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Подлежащие — одна черта, Сказуемое — две черты обстоятельство — точка пунктир Дополнение — пунктир.

Подлежащее одной чертой, сказуемое двумя, обстоятельство : _. _. _. В общем обстоятельство точка — тире, а дополнение пунктирной линией : — — — -.

Решение задачи во вложенном файле.

В прямоугольном ∆ АВС∠С = 90°, высота СК делит гипотенузу на отрезки АВ = 5 см, кВ = 1 см. Определите длину высоты СК. Высотапрямоугольноготреугольника, проведеннаяк гипотенузе, естьсреднеегеометрическое (среднеепропорциональное) между отрезками, н..

Так наверное, но это не точно)0).

Вот как то так этт 1.

1) Треугольники А2КВ2 и А1КВ1 подобны, так как плоскости α и β параллельны (дано), значит и отрезки А1В1 и А2В2 параллельны. Из подобия имеем : А2В2 / А1В1 = КВ2 / КВ1 = 9 / 4. Отсюда КВ2 = 18см. Тогда В1В2 = КВ2 — КВ1 или В1В2 = 18 — 8 = 10см. О..

По теореме Пифагора BD ^ 2 = BC ^ 2 + CD ^ 2. BD ^ 2 = 4x ^ 2 — x ^ 2. BD ^ 2 = 3x ^ 2BD = x корней из 3. Но CD ^ 2 = BD * AD. X ^ 2 = x корней из 3 * AD. AD = (х корей из 3) / 3. АВ = х корней их 3 + (х корней из 3) / 3 = (4х корней из 3) / 3.

🌟 Видео

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Разбор Задачи №16 из Варианта Ларина №271Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия. ОГЭ по математике. Задание 15Скачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать

Центр описанной окружности.Скачать

ЕГЭ Задание 16 Первый признак подобия треугольниковСкачать

№16 из ЕГЭ2022 и олимпиады. Красивое доказательство свойства ортоцентра остроугольного треугольникаСкачать