Радиус окружности равен 20. Найдите величину острого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.
По теореме синусов для треугольника ACB имеем:
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Хорды и дуги
Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.
При этом будем иметь в виду дуги, меньшие полуокружности.
Теорема 1. Равные дуги стягиваются равными хордами.
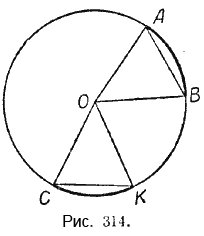
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (рис. 314).
Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.
Теорема 2 (обратная). Равные хорды стягивают равные дуги.
Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (рис. 314).
Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: (breve = breve).
Теорема 3. Большая дуга стягивается и большей хордой.
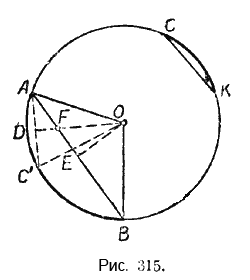
Пусть дуга АВ больше дуги СК (рис. 315).
Требуется доказать, что хорда АВ больше хорды СК.
Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С’ на дуге АВ между точками Aи В, дуга СК примет положение дуги АС’, а хорда СК примет положение хорды АС’. Проведём радиусы в точки A, В и С’. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС’. В треугольнике ОFE отрезок ОЕ — катет, а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.
Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.
Теорема 4 (обратная). Большая хорда стягивает и большую дугу.
Пусть хорда А В больше хорды СК.
Требуется доказать, что дуга АВ больше дуги СК (рис. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:
Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.
Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, (breve > breve).
Свойство дуг, заключенных между параллельными хордами
Теорема. Дуги, заключённые между параллельными хордами, равны.
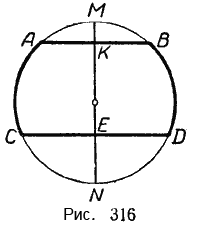
Пусть хорда AB параллельна хорде СD (рис. 316).
Требуется доказать, что (breve = breve). Проведём диаметр MN ⊥ AB. Так как CD || AB, то MN ⊥ CD.
Перегнём чертёж по диаметру MN так, чтобы правая часть совпала с левой.
Тогда точка В совпадёт с точкой А, так как они симметричны относительно оси MN (AB ⊥ MN по построению и AK = KB).
Аналогично, точка D совпадёт с точкой С. Отсюда (breve = breve).
Свойство дуг, заключённых между касательной и параллельной ей хордой
Теорема. Дуги, заключённые между касательной и параллельной ей хордой, равны.
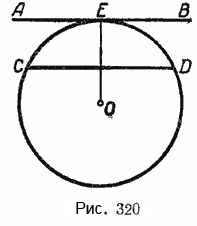
Пусть касательная АВ и хорда СD параллельны. Точка Е — точка касания прямой АВ с окружностью О (рис. 320).
Требуется доказать, что (breve = breve).
Для доказательства соединим точку касания Е с центром круга.
OE ⊥ AB, а так как СD || АВ, то OE ⊥ CD, а перпендикуляр к хорде, проведённый из центра той же окружности, делит стягиваемую ею дугу пополам.
Следовательно, (breve = breve).
Видео:ГЕОМЕТРИЯ (урок 14) окружности, дуги, хордыСкачать

Диаметр, перпендикулярный к хорде
Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
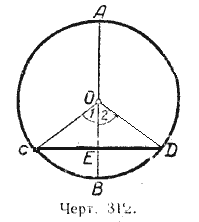
Пусть диаметр AB перпендикулярен к хорде CD (черт. 312). Требуется доказать, что
$$ CE = ED, breve = breve, breve = breve $$
Соединим точки С и D с центром окружности О. В равнобедренном треугольнике СОD отрезок ЕО является высотой, проведённой из вершины О на основание CD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и ∠1 = ∠2. Но ∠1 и ∠2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
$$ breve = breve $$
Дуги CA и ВА также равны между собой, как дополняющие равные дуги до полуокружности.
Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.
Пусть диаметр AB делит хорду CD пополам. Требуется доказать, что AB ⊥ CD,
Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, AB⊥CD, а отсюда (по теореме 1) следует, что
$$ breve = breve; breve = breve $$
Теорема 3 (обратная). Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.
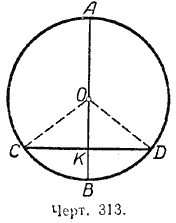
Пусть диаметр AB делит дугу СВD пополам (черт. 313). Требуется доказать, что
Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы (breve) = (breve), поэтому ОК будет и медианой и высотой этого треугольника. Следовательно, диаметр AB проходит через середину хорды и перпендикулярен к ней.
Видео:Радиус и диаметрСкачать

ГДЗ по геометрии 9 класс Зив дидактические материалы Контрольные работы К-4. Варианты — 2
Издательство: Просвещение 2015
Тип: Дидактические материалы
Подробный решебник (ГДЗ) по Геометрии за 9 (девятый) класс дидактические материалы — готовый ответ Контрольные работы К-4. Варианты — 2. Авторы учебника: Зив. Издательство: Просвещение 2015.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Похожие ГДЗ
ГДЗ Задачник геометрия 7-11 класс Зив Б.Г.
К—4 Вариант 2 1. Около правильного треугольника описана окружность и в него вписана окружность. Длина меньшей окружности равна 8я. Найдите площадь кольца и площадь треугольника. 2. Хорда окружности равна 6 и стягивает дугу в 60°. Найдите длину дуги и площадь соответствующего сектора. 3. На рисунке 57 хорды CD и СН стягивают дуги в 90°. Радиус окружности равен R. Найдите площадь заштрихованной фигуры. с 4*. На сторонах правильного 8-угольника А1А2. А8 вне его построены квадраты. Докажите, что многоугольник, образованный вершинами этих квадратов, отличных от Ах, А2, А3, . Ag, является правильным. Рис. 57
📸 Видео
Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Равные хорды, равные дугиСкачать

Радиус Хорда ДиаметрСкачать

Геометрия Докажите, что если две дуги окружности равны, то равны и хорды, их стягивающиеСкачать
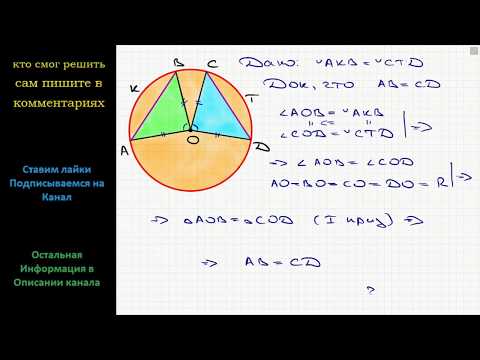
Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать

Задача на нахождение длины хорды окружностиСкачать

РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Окружность. Как найти Радиус и ДиаметрСкачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

ОГЭ Задание 16. Окружность, хорды, дуги, вписанные и центральные углыСкачать

Окружнось. Зависимость длины хорды, от длины дуги.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать