Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
- Построение отрезка, равного данному
- Деление отрезка пополам
- Построение угла, равного данному
- Построение перпендикулярных прямых
- Пример 1
- Пример 2
- Построение параллельных (непересекающихся) прямых
- Построение правильного треугольника, вписанного в окружность
- Построение правильного четырехугольника вписанного в окружность
- Вариант 1
- Вариант 2
- Построение вписанного в окружность правильного пятиугольника
- Построение правильного шестиугольника, вписанного в окружность
- Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
- 🎬 Видео
Видео:Построить описанную окружность (Задача 1)Скачать

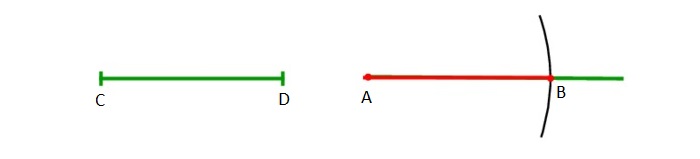
Построение отрезка, равного данному
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

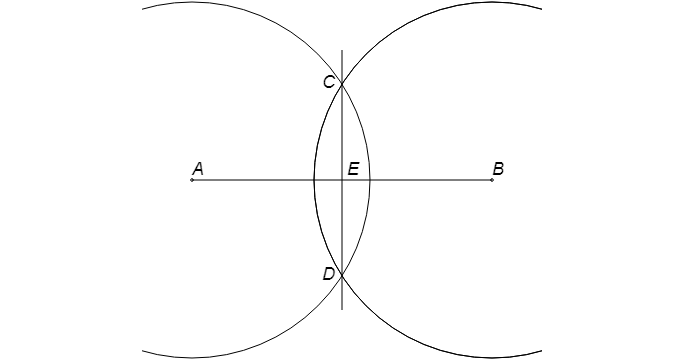
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

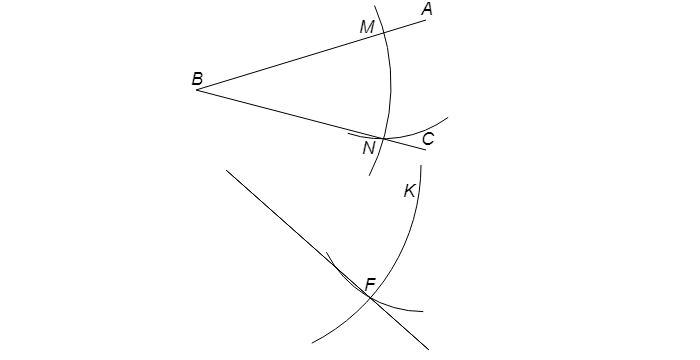
Построение угла, равного данному
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Построение перпендикулярных прямых
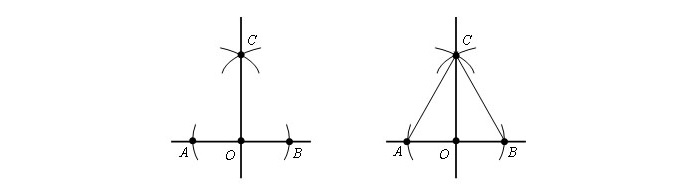
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Видео:Геометрия - Построение правильного треугольникаСкачать

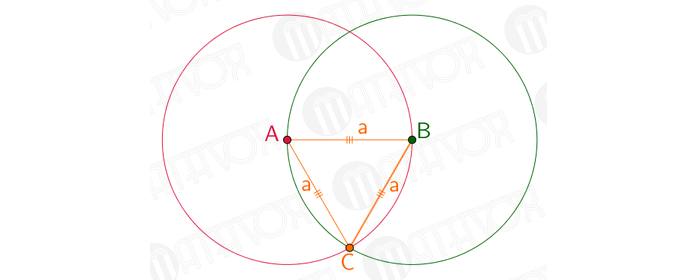
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

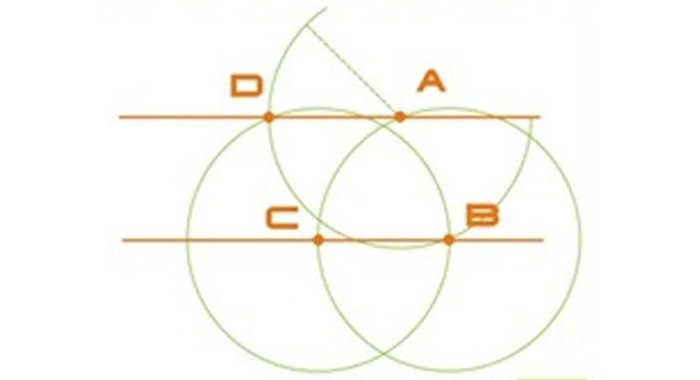
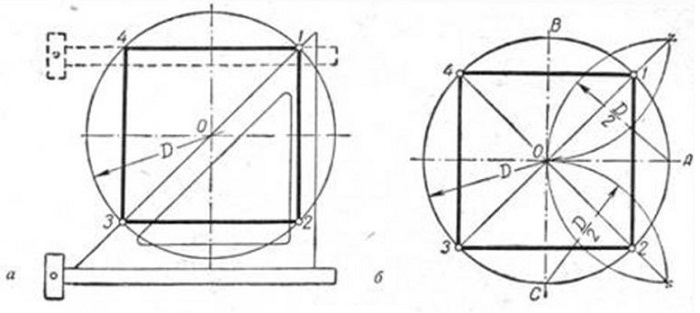
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Видео:Построение равностронего треугольника.Скачать

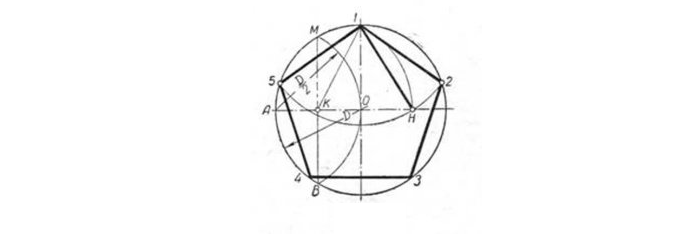
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Видео:Построение 8 угольника циркулемСкачать

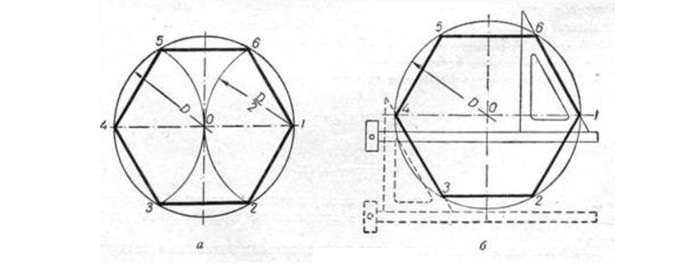
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
Видео:Вписанная и описанная окружностиСкачать

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
Видео:Построение пятиугольника циркулемСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
🎬 Видео
Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Построение медианы в треугольникеСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать