- Ваш ответ
- Похожие вопросы
- Что такое хорда окружности в геометрии, её определение и свойства
- Как построить геометрическую хорду
- Свойства
- Взаимосвязь с радиусом и диаметром
- Хорда и радиус
- Отношения со вписанными углами
- Взаимодействия с дугой
- Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3?
- Постройте окружность?
- Через точку М, находящуюся на расстоянии 15см от центра окружности радиусом 17 см, проведена хорда CD, которая делится точкой М на отрезки CM : MD = 1 : 4?
- Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см?
- Через точку М, находящуюся на расстоянии 15 см от центра окружности, проведена хорда, которая делится точкой М в отношении 1 : 4?
- Через точку А, находящующуюся на расстоянии 5 см от центра на окружности, радиуса 11 см проведена хорда, которую точка А делит на отрезки длины, которых относятся как 2 : 3?
- Диаметр СD окружности с центром в точке О пересекается с хордой AB в точке К, OK = 5 см?
- Точка M удалена на 20 см от центра окружности, радиус которой равен 22 см?
- В окружности проведена хорда длинной 10 см?
- Проведена окружность с центром в точке О?
- Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см?
Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Ваш ответ
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,036
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Что такое хорда окружности в геометрии, её определение и свойства
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Видео:Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Хорда и радиус
Между этими понятиями существуют следующие связи:
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Видео:Радиус Хорда ДиаметрСкачать

Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Видео:Длина окружности. Математика 6 класс.Скачать

Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3?
Геометрия | 5 — 9 классы
Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3.
Найдите длину этой хорды.
Расстояние между точками О и А : ОA = 5 (дано).
Хорда BC = BA + AC или BC = 2х + 3х = 5х.
Радиус DO = OE = 11 (дано).
DA = DO + OA или DA = 16см.
АЕ = ОЕ — ОА или АЕ = 6см.
По свойству пересекающихся хорд DA * AE = 2X * 3X или
(DO + OA) * AE = 6X² или 16 * 6 = 6X².
Отсюда Х = 4см и хорда
Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Постройте окружность?
Длина хорды 16см.
Центр хорды удалён от центра окружности на 6 см.
Вычислите радиус и диаметр окружности.
Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Через точку М, находящуюся на расстоянии 15см от центра окружности радиусом 17 см, проведена хорда CD, которая делится точкой М на отрезки CM : MD = 1 : 4?
Через точку М, находящуюся на расстоянии 15см от центра окружности радиусом 17 см, проведена хорда CD, которая делится точкой М на отрезки CM : MD = 1 : 4.
Найдите хорду CD.
Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см?
Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см.
Найдите расстояние от точки Р до Центра окружности, если её радиус равен 6 см.
Видео:В окружности с центром O AC и BD – диаметры ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Через точку М, находящуюся на расстоянии 15 см от центра окружности, проведена хорда, которая делится точкой М в отношении 1 : 4?
Через точку М, находящуюся на расстоянии 15 см от центра окружности, проведена хорда, которая делится точкой М в отношении 1 : 4.
Радиус окружности равен 17 см.
Найти длину этой хорды.
Пожалуйста с рисунком.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Через точку А, находящующуюся на расстоянии 5 см от центра на окружности, радиуса 11 см проведена хорда, которую точка А делит на отрезки длины, которых относятся как 2 : 3?
Через точку А, находящующуюся на расстоянии 5 см от центра на окружности, радиуса 11 см проведена хорда, которую точка А делит на отрезки длины, которых относятся как 2 : 3.
Найдите длину этой хорды.
Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Диаметр СD окружности с центром в точке О пересекается с хордой AB в точке К, OK = 5 см?
Диаметр СD окружности с центром в точке О пересекается с хордой AB в точке К, OK = 5 см.
Расстояние от центоа окружности до хорды равно 4см.
Найдите радиус окружности, если длина хорды равна 16 см.
Видео:Вариант #20 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

Точка M удалена на 20 см от центра окружности, радиус которой равен 22 см?
Точка M удалена на 20 см от центра окружности, радиус которой равен 22 см.
Через эту точку проведена хорда длинной 20 см.
Найдите длины отрезков, на которые делит точка M данную хорду.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

В окружности проведена хорда длинной 10 см?
В окружности проведена хорда длинной 10 см.
Радиус окружности равен 13 см.
Найдите расстояние от центра окружности до хорды.
Видео:ВСЯ ГЕОМЕТРИЯ НА ОГЭ ЗА 3 ЧАСА | Математика ОГЭ 2023 | УмскулСкачать

Проведена окружность с центром в точке О?
Проведена окружность с центром в точке О.
Хорда АВ = 10 см, угол АОВ = 90°.
Найдите расстояние от точки О до хорды АВ.
Видео:Окружности #3. Геометрия ОГЭ ФИПИ 🔴Скачать

Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см?
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см.
На этой странице вы найдете ответ на вопрос Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.
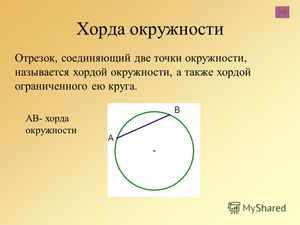 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.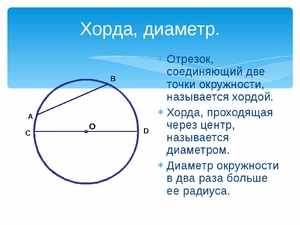 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.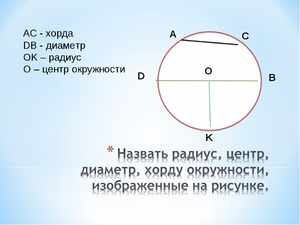 Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.






