С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Углы ромба через сторону и высоту
- 2. Углы ромба ромба через площадь и высоту
- 3. Углы ромба через площадь и сторону
- 4. Углы ромба через диагонали
- 5. Углы ромба через сторону и диагональ
- 6. Углы ромба через сторону и радиус вписанной окружности
- Радиус и угол ромба
- Свойства
- В окружность вписан ромб найти угол
- 🔍 Видео
Видео:№539. В треугольник MNK вписан ромб MDEF так, что вершины D, Е и F лежат соответственноСкачать

1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).
 |
Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac ) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac=frac.) | (3) |
| (small sin alpha=frac) | (4) |
| (small alpha=mathrmfrac) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).
 |
Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac, ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac=mathrmfrac<large frac | (9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).
 |
Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
| ( small alpha= mathrmfrac=mathrmfrac<large frac |
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac. ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.
 |
| (small h=frac<large sqrt>.) | (11) |
| (small a=frac<large sqrt>.) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac) ( small =frac<frac<large sqrt>><frac<large sqrt>> ) ( small =frac .) | (13) |
| (small alpha=mathrm frac .) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).
 |
Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac .) Тогда для треугольника AOB имеют места следующие равненства:
| (small frac=sin frac,) |
| (small frac=cos frac) |
| (small sin frac=frac) | (15) |
| (small cos frac=frac.) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac=±sqrt<frac>,) | (17) |
| (small cosfrac=±sqrt<frac>.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac,) | (19) |
| (small cos beta=2cdot sin^2 frac-1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac,) | (21) |
| (small cos beta=frac-1.) | (22) |
| (small alpha=mathrm left(1- frac right),) | (23) |
| (small beta=mathrm left( frac-1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.
 |
В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac) | (26) |
| (small alpha=mathrmfrac) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
Видео:Геометрия В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиусСкачать

Радиус и угол ромба
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Свойства
Радиус вписанной окружности, представляющий собой половину высоты, теоретически участвует в образовании прямоугольного треугольника, из которого можно найти сторону ромба, как отношение удвоенного радиуса к синусу угла α. a=2r/sin〖α 〗
Высота ромба будет равна удвоенному радиусу вписанной окружности. Площадь, ка произведение высоты и стороны ромба, через радиус вписанной окружности и угол α будет представлена произведением соответствующих выражений. Чтобы вычислить периметр, нужно будет эквивалент стороны умножить на четыре. h=2r S=(4r^2)/sin〖α 〗 P=8r/sin〖α 〗
Видео:Площадь ромба. Легче понять...Скачать
В окружность вписан ромб найти угол
Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке возрастания.
Введём обозначения, как показано на рисунке. Имеем:
Тогда
Высота делит сторону на два отрезка, и в ответе требуется указать длины обоих отрезков. Длина первого отрезка 17, и длина второго отрезка 17, поэтому ответ 1717.
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Пусть a сторона ромба, h — его высота. Все стороны ромба равны, поэтому Площадь ромба можно найти как произведение стороны на высоту:
Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.
Проведём диагональ OQ Рассмотрим треугольник OQR, OQ и OR равны как радиусы окружности. Все стороны ромба равны, поэтому OR = QR, получаем, что OQ = QR = OR, следовательно, треугольник OQR — равносторонний, поэтому все его углы, в том числе и угол ORQ, равны 60°.
Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах.
Проведём диагональ TO Рассмотрим треугольник OTV, TO и OV равны как радиусы окружности. Все стороны ромба равны, поэтому TV = OV, получаем, что OV = TV = TO, следовательно, треугольник OTV — равносторонний, поэтому все его углы, в том числе и угол OTV, равны 60°. Аналогично, треугольник STO — равносторонний и угол STO равен 60°. Таким образом, угол STV равный сумме углов STO и OTV равен 120°.
🔍 Видео
Геометрия В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делитСкачать
№700. Докажите, что в любой ромб можно вписать окружность.Скачать

№405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы,Скачать
Геометрия, номера 45.1, 46.1 (радиус вписанной окружности)Скачать

в ромбе abcd угол dab равен 36 найдите угол dbcСкачать

ОГЭ 2020 задание 16Скачать
Геометрия В ромб с острым углом 30 вписан круг, площадь которого равна Q. Найти площадь ромбаСкачать

Найти угол треугольника, вписанного во вписанную окружностьСкачать

ОКРУЖНОСТЬ (радиус окружности, вписанной в ромб) ЧАСТЬ 11Скачать
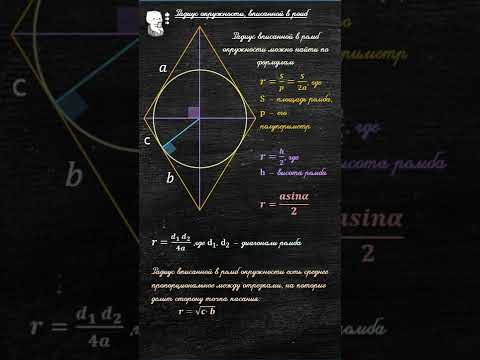
Радиус вписанной в ромб окружности (6701)Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

