В одной окружности проведены хорды ad

Геометрия | 5 — 9 классы

В одной окружности проведены хорды AD и BF, пересекающиеся в точке К.

Найдите длину отрезка ВК, если АК = 8, DK = 3, FK = 4.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Из точки А, взятой на окружности, проведены диаметр АВ = 10 см и хорда АС Из точки В проведены к хорде перпендикуляр длиной 6 и касательнвя, пересекающая продолжение хорды в точке Д?

Из точки А, взятой на окружности, проведены диаметр АВ = 10 см и хорда АС Из точки В проведены к хорде перпендикуляр длиной 6 и касательнвя, пересекающая продолжение хорды в точке Д.

Найти длину касательной.

Видео:Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делиться на отрезки 3 см и 12 см, а другая пополам.

Найдите длину второй хорды.

Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Из точки А к окружности проведены касательные АВ и АС, где В и С — точки касания?

Из точки А к окружности проведены касательные АВ и АС, где В и С — точки касания.

Через точку F этой окружности проведена ещё одна касательная, которая пересекает лучи АВ и АС в точках К и О соответственно, КО = 6 см.

Вычислите длины отрезков ВК и ОС.

Видео:В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать

Две хорды одной окружности пересекаются в точке делящей одну хорду на отрезки 2 см и 16 см а другую на отрезки один из которых в 2 раза больше другого найдите длину второй хорды?

Две хорды одной окружности пересекаются в точке делящей одну хорду на отрезки 2 см и 16 см а другую на отрезки один из которых в 2 раза больше другого найдите длину второй хорды.

Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

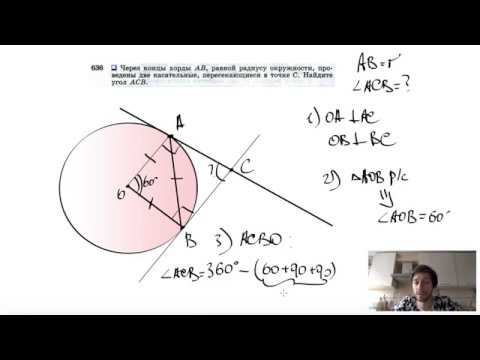
В окружности проведены хорды ав и сд пересекаются в точке к, кс = 6 ак см, ак = 8 вк + дк = 21 см найдите длины вк и дк?

В окружности проведены хорды ав и сд пересекаются в точке к, кс = 6 ак см, ак = 8 вк + дк = 21 см найдите длины вк и дк.

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делится на отрезки 2 см и 6 см, а длина другой хорды 7 см.

Найдите отрезки второй хорды.

Видео:Геометрия В окружности проведены две хорды AB = a и AC = b. длина дуги AC вдвое больше длины дуги ABСкачать

К окружности с диаметром АС проведена касательная ВС?

К окружности с диаметром АС проведена касательная ВС.

Отрезок АВ пересекает окружность в точке D.

Через точку D проведена еще одна касательная к окружности, пересекающая отрезок ВС в точке К.

Найдите длину отрезка СК, если ВС = 6.

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

В окружности проведены две пересекающиеся хорды?

В окружности проведены две пересекающиеся хорды.

Одна из них делится на отрезки 3см и 12см, а другая — пополам.

Найдите длину второй хорды.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

В одной окружности проведены хорды AC и BE, пересекающиеся в точке M?

В одной окружности проведены хорды AC и BE, пересекающиеся в точке M.

Найдите длину отрезка AM если CM = 2, BM = 6, EM = 4.

Видео:Геометрия В окружности проведены диаметры AB и CD. Докажите, что AC = BD и AC ll BDСкачать

Две равные окружности пересекаются в точках А и В?

Две равные окружности пересекаются в точках А и В.

Через точку А проведена хорда АМ одной окружности, а через точку В — хорда ВN другой окружности, причем АМ и BN параллельны.

Доказать, что эти хорды равны.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос В одной окружности проведены хорды AD и BF, пересекающиеся в точке К?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

В одной окружности проведены хорды ad

Вопрос по геометрии:

В одной окружности проведены хорды AD и BF, пересекающиеся в точке К. Найдите длину отрезка ВК, если АК=8, DK=3, FK=4

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№645. Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательнойСкачать

Касательная к окружности

О чем эта статья:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🎥 Видео

В окружности три хордыСкачать

№667. Диаметр АА1 окружности перпендикулярен к хорде ВВ1 и пересекает ее в точке С. Найдите BB1Скачать

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°.ОГЭ МатематикаСкачать

Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать