Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать
Окружность, вписанная в правильный многоугольник
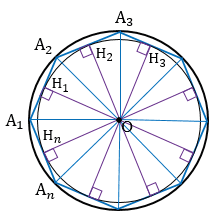
Теорема
| В любой правильный многоугольник можно вписать окружность, и притом только одну. |
Доказательство
Доказать: в многоугольник А1А2А3. Аn можно вписать окружность, и притом только одну.
Доказательство:
А1ОА2 = А2ОА3 = . = А1ОАn по трем сторонам (ОА1 = ОА2 = . = ОАn, как радиусы описанной окружности и А1А2 = А2А3 = . = АnА1, как стороны правильного многоугольника), тогда и высоты этих треугольников, проведенные из вершины О, также будут равны: ОН1 = ОН2 = . = ОНn. Следовательно, окружность с центром О и радиусом ОН1 проходит через точки Н1, Н2, . , Нn и касается сторон многоугольника в этих точках, т.е. эта окружность вписана в данный правильный многоугольник А1А2А3. Аn.
Докажем, что вписать можно только одну окружность.
Пусть существует окружность с центром О1, вписанная в многоугольник А1А2А3. Аn, отличная от окружности с центром О и радиусом ОН1. Тогда ее центр О1 равноудален от сторон многоугольника, т.е. точка О1 лежит на каждой из биссектрис углов многоугольника А1А2А3. Аn и, следовательно, совпадает с точкой О пересечения этих биссектрис (смотри теорему об окружности, описанной около правильного многоугольника). Радиус этой окружности равен расстоянию от точки О до сторон многоугольника,т.е. равен ОН1. Значит, получаем, что вторая окружность совпадает с первой. Следовательно, наше предположение неверно, и в правильный многоугольник вписать можно только одну окружность. Теорема доказана.
Следствие 1
| Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. |
Следствие 2
| Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. |
Эта точка называется центром правильного многоугольника.
Поделись с друзьями в социальных сетях:
Видео:Если в четырёхугольник можно вписать окружностьСкачать
Окружность, вписанная в правильный многоугольник
На этом занятии мы рассмотрим следующую тему – «Окружность, вписанная в правильный многоугольник». В первую очередь дадим определение правильному многоугольнику. После чего докажем теорему о том, что внутри любого правильного многоугольника можно вписать окружность, и притом только одну. Кроме того, рассмотрим следствия из этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
💥 Видео
№700. Докажите, что в любой ромб можно вписать окружность.Скачать
111. Окружность, вписанная в правильный многоугольникСкачать
Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать
110. Окружность, описанная около правильного многоугольникаСкачать
9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать
Вписанная и описанная окружность - от bezbotvyСкачать
Окружность, вписанная в правильный многоугольник | Геометрия 7-9 класс #106 | ИнфоурокСкачать
В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Окружность, вписанная в правильный многоугольник. Видеоурок по геометрии 9 классСкачать
Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать
Как найти площадь многоугольника? | 1 задание ЕГЭ профиль #егэпрофиль #профиль #умскул #егэСкачать
Урок 1. Вписанная окружность в четырехугольник. Теория+ практикаСкачать
ЕГЭ. Описывающая многоугольник окружность.Скачать
9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать
Правильные многоугольники. Урок 11. Геометрия 9 классСкачать
