Дополнительные построения в треугольнике (8 видео)

Дополнительные построения в треугольнике

Дополнительные построения занимают важное место среди различных методов решения геометрических задач. Например, теорема о площади треугольника, теорема Пифагора, теорема о пересечении высот треугольника и многие другие. При подготовке к экзамену по математике большинство задач по планиметрии не решается с помощью строгих алгоритмов, почти каждая геометрическая задача требует своего подхода.

Искусство решать задачи основывается на хорошем знании теории, на знании достаточного количества геометрических фактов и в овладении приёмами и методами решения.

Эти методы обладают некоторыми особенностями:

большое разнообразие, трудность формального описания, взаимозаменяемость, отсутствие чётких границ области применения.

При решении геометрических задач используются три основных метода:

геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Во многих случаях решать задачи помогает введение в чертеж дополнительных линий — так называемые дополнительные построения. Такие дополнительные построения, вводящие новые углы и новые отрезки, иногда приводят к появлению геометрических фигур, облегчающих решение задачи. Представленные данные говорят об актуальности изучения метода дополнительных построений.

Объект исследования: планиметрические задачи

Предмет исследования: метод дополнительных построений

·выяснить, в чем состоит суть метода дополнительных построений;

узнать, при решении каких задач целесообразно использовать метод дополнительных построений.

выявить, при решении каких задач метод дополнительных построений является наиболее эффективным;
изучить разнообразные методы, которые могут быть успешно применены при решении многих геометрических задач;
провести группировку различных видов дополнительного построения;

В процессе работы я использовала следующие методы исследования:

анализ математической и методической литературы;
анализ геометрических задач, которые предлагались на ЕГЭ и ОГЭ;
классификация дополнительных построений;
математическое моделирование;

-поиск рационального способа решения задачи методом дополнительного построения.

Теоретическая значимость: исследовательская работа позволяет расширить знания о методе дополнительных построений при решении геометрических задач.

Практическая значимость работы заключается в возможности использования ее результатов учениками, учителями математики.

Глава 1. Дополнительное построение как метод решения планиметрических задач

Приёмы дополнительного построения

Решение геометрической задачи начинается с работы над чертежом. Часто на чертеже, особенно в геометрических задачах, которые предлагаются на различных олимпиадах, трудно заметить связи между данными и искомыми величинами. В подобных ситуациях решить задачу помогают дополнительные линии, которые проводятся для того, чтобы свести задачу к ранее решенной или более простой задаче. Они позволяют включить в задачу новые фигуры с их свойствами, тем самым увеличить число теорем, которые можно использовать при решении задачи.

Приёмы дополнительного построения, которые используются при решении геометрических задач можно разделить на два вида — это разбиение фигур и дополнение.

проведение в многоугольнике прямой, параллельной одной из имеющихся (или параллельных прямых), что позволяет применять подобие;
разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;
проведение перпендикуляров, радиусов окружности в точки касания, высот в трапеции позволяют получить прямоугольные треугольники.

построение параллелограмма, с помощью продления медианы треугольника, что позволяет применять свойства параллелограмма;
построение дополнительного треугольника;
построение вспомогательной окружности с целью применения свойств хорд, касательных и углов, связанных с окружностью.

Рассмотрим дополнительные построения, использование которых целесообразно при решении планиметрических задач, связанных с треугольниками и четырёхугольниками [4].

1.2.1.Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Если в треугольнике известен отрезок АА1, то через точку А1 проводится прямая, параллельная стороне АВ, до её пересечения со стороной АС (рис.1). По теореме о пропорциональных отрезках получаем . Если отрезок АА1 является медианой, то по теореме Фалеса А2 – середина стороны АС.

Если в треугольнике известны два отрезка, проведённые из разных вершин, в том числе биссектриса, высота, или медиана, то через основание одного из них проводится прямая, параллельная данному отрезку, до её пересечения со стороной треугольника (рис. 2, рис.3). Так на рис. 2 прямая КB2 отсекает от треугольника AA1A2 подобный ему треугольник AКB2, а прямая A1A2 – треугольник CA1A2, подобный треугольнику CBB2.

1.2.2.Разбиение фигуры на части для получения треугольника и параллелограмма

Если в треугольнике (рис. 4), параллелограмме (рис. 5) или трапеции (рис. 6, рис. 7) дана биссектриса одного из внутренних углов, то можно построить ромб, две стороны которого лежат на сторонах данного треугольника или четырехугольника, а биссектриса является диагональю. Такое построение позволяет использовать свойства этих фигур.

Проведённые перпендикуляры позволяют получить прямоугольные треугольники и использовать теорему Пифагора, теоремы о подобии треугольников.

Часто в задачах используются такие дополнительные построения как проведение радиусов окружности в точки касания, высот в трапеции.

Так, если в условии задачи известна медиана треугольника, то удвоив её, мы получим параллелограмм (рис.8), что позволит использовать его свойства [8].

В зависимости от содержания задачи такое дополнительное построение можно выполнять и для двух, и для трёх медиан; использовать не весь параллелограмм, а только его части Например, треугольника АА2С (рис. 8).

1.3.2.Дополнительное построение треугольника

В результате построения, выполненного на рис. 9 (АВ2 ||ВС) и рис. 10 (АС||ВА2), появляются две пары подобных треугольников. Так, на рисунке 9 ?AКB2 и ?A1КB; ?AB1B2 и ?CB1B; на рис. 10 ?AКB1 и ?A2КВ; ?AA1C и ?A2A1B подобны.

На рис. 11 и рис 12 (АМ1|| ВС, L1=КМ∩ВС) ? ALМ1 подобен ? BLL1, ? AMM1 подобен ?CML1, ? AКM1 подобен ?КA1L1.

Если даны две окружности разных радиусов (не имеющие общих точек, пересекающиеся в двух точках или касающиеся внешним образом) с секущей, проходящей через одну из точек пересечения окружностей (или общей касательной), то через центр меньшей окружности проводится прямая, параллельная данной секущей (или касательной). Находится точка пересечения с радиусом большей окружности, проведённым в точку касания, или с его продолжением (рис. 13, рис. 15, рис. 14, рис. 16).

Результатом этих дополнительных построений является прямоугольный треугольник. В треугольнике вершины острых углов совпадают с центрами данных окружностей, один из катетов равен половине отрезка секущей, расположенного внутри окружностей (или отрезку касательной, заключенному между точками касания), а другой сумме (для случая с внутренней касательной) или — разности (для случая с внешней касательной) радиусов этих окружностей. В случае касания данных окружностей (рис. 15) гипотенуза O1O2 ?O1O2В равна сумме радиусов этих окружностей (r1 и r2), поэтому расстояния между точками касания окружностей с их общей внешней касательной можно найти по формуле А1А2=2

Прямоугольный треугольник достраивается до равнобедренного треугольника/

Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника. Один из катетов данного треугольника становится, медианой, биссектрисой и высотой, а другой – половиной основания.

Если дана трапеция, то с помощью продолжения боковых сторон она достраивается до треугольника.
Если в треугольнике, параллелограмме или трапеции дана биссектриса одного из внутренних углов, то проводится дополнительное построение треугольника, одна из сторон

которого содержит эту биссектрису, вторая совпадает со стороной данной фигуры, а третья или параллельна другой стороне этой фигуры, или получается при ее продолжении (рис. 17– рис. 20). Построенный треугольник является равнобедренным.

1.3.3. Построение дополнительной окружности

Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы.

Если дан четырехугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность. Признаком существования для четырехугольника описанной окружности обладают квадрат, прямоугольник и равнобедренная трапеция.

Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него вписывается окружность.

Если даны две окружности с общей внешней касательной, касающиеся друг друга внешним образом, то в рассмотрение вводится треугольник, вершинами которого служат три точки касания данных фигур (рис.21).

Треугольник АА1А2 является прямоугольным с прямым углом А (А – точка касания окружностей). Докажем, что угол A1AA2 = 90°.

?O1AA1 и ?O2AA2 – равнобедренные. Пусть α и β углы при основаниях этих треугольников; тогда 2α – внешний угол при вершине O1, 2β – внешний угол при вершине O2. 2α и 2β — односторонние углы при O1A1 || O2A2 и секущей O1O2, значит 2α + 2β = 180°, поэтому α + β =90°. ?A1AA2 = 180° – (LA1AO1 +LA2AO2) = 180° – (α + β) = 180° – 90°, что и требовалось доказать.

Глава 2 Практическое применение метода дополнительных построений.

2.1. Решение задач методом дополнительных построений

Задача 1. Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Две стороны треугольника равны 10см и 15см, угол между ними равен 600. Найти длину биссектрисы, проведённой из данного угла.

Δ АВС, АВ= 10см, АС = 15см,

Содержание

Старт в науке
Дополнительные построения в планиметрии
Задачи с окружностями
Задачи с несколькими вариантами дополнительного построения
Задачи с разрозненными данными
исследовательская работа «Решение задач по геометрии методом дополнительных построений»
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
📹 Видео

Старт в науке

Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».

Видео:ЛШУ2023. Дополнительные построения в геометрии. Прокопенко Дмитрий ВикторовичСкачать

Дополнительные построения в планиметрии

Задачи с окружностями

С помощью дополнительного построения окружности часто решаются задания № 24 и № 26 ОГЭ, а также № 16 ЕГЭ.

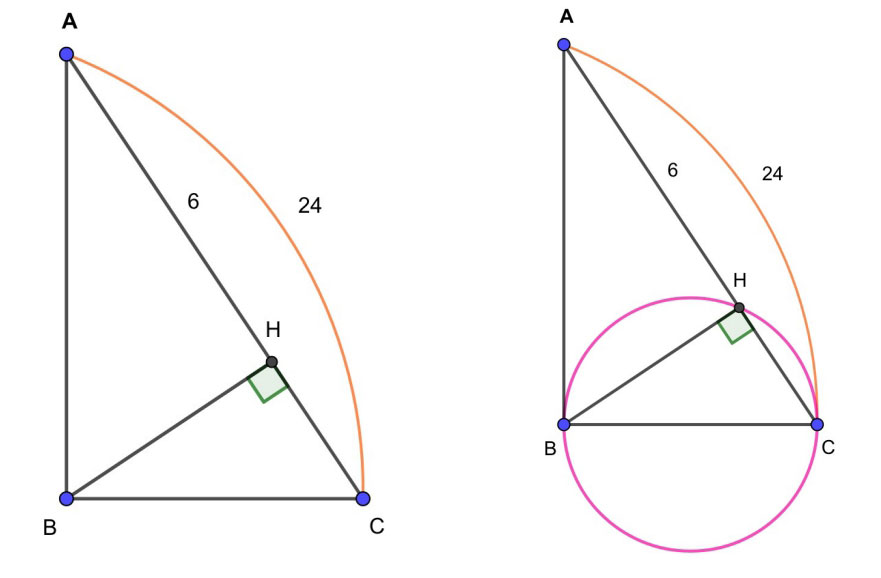
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.

Строим окружность вокруг треугольника ВНС. Центр этой окружности является и серединой ВС. ВС — диаметр. АС по отношению к данной окружности — секущая. АВ — отрезок касательной. АН — внешняя часть секущей. Все это подводит к теореме о квадрате касательной.

АВ 2 — произведение секущей на ее внешнюю часть. Следовательно, нужно умножить AH на AC. 6×24 = 144 (это АВ в квадрате). АВ=12. Больше заданий для подготовки к ОГЭ вы найдёте в учебнике «Геометрия. 9 класс».

Задачи с несколькими вариантами дополнительного построения

В условиях задания № 16 ЕГЭ пункт «б» может подсказать, какое решение задачи будет более удачным.

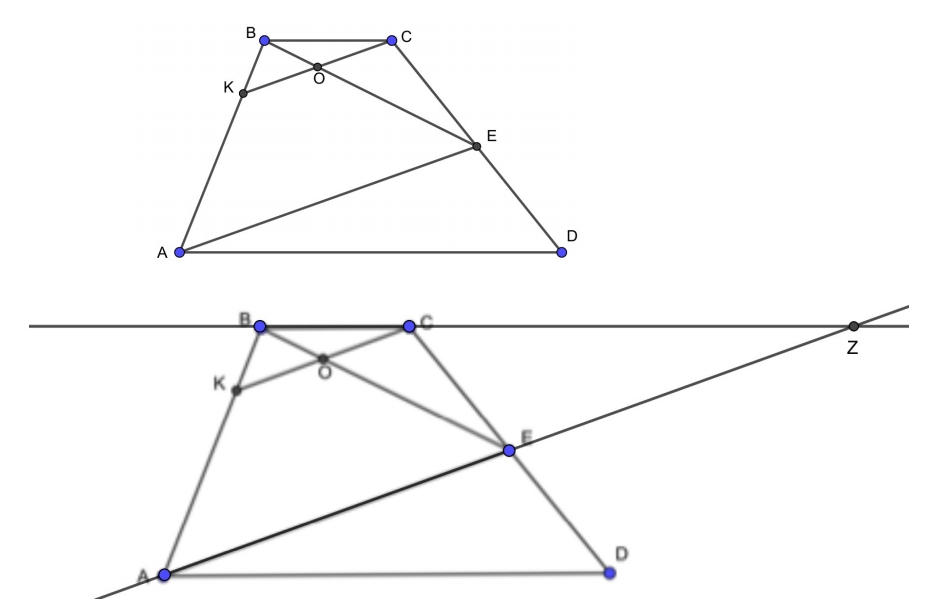
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO=KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

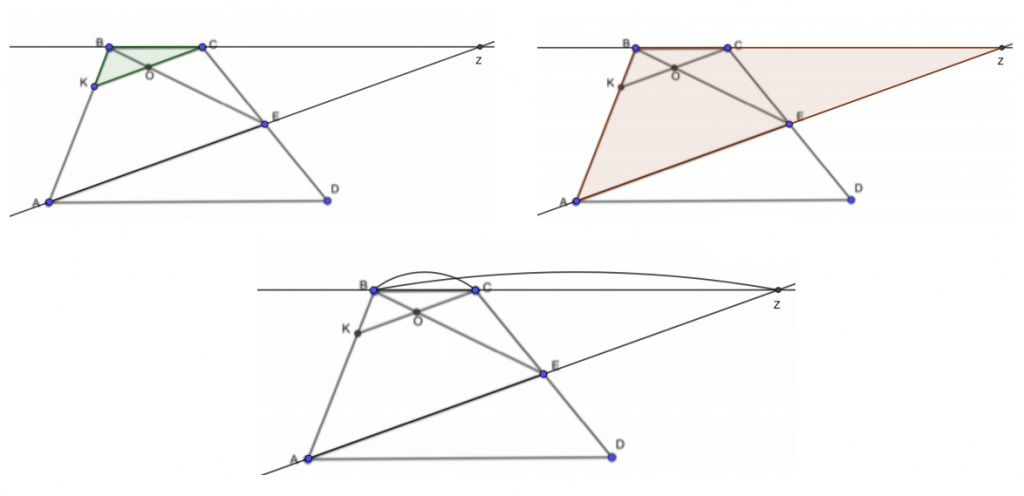
Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO.

Площадь треугольника ABZ такая же, как площадь трапеции ABCD за счет равенства треугольников АЕD и ZЕC. Треугольник КВС подобен треугольнику ABZ. Как известно, отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отрезок BC, деленый на отрезок BZ, равен 3:10. На отрезок СZ приходится 7 частей. Ответ в пункте «б»: 3:7.

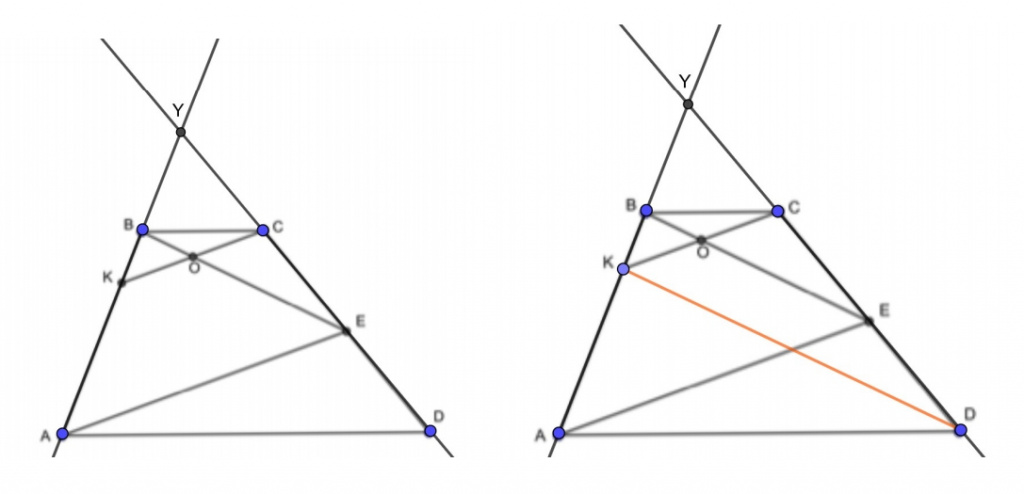
Второй вариант построения. Продолжим стороны AB и CD. Используя теорему, обратную теореме Фалеса, доказываем, что KB относится к BY так же, как YE к ED, и что отрезок KD параллелен BE. В треугольнике KCD видна середина CD. Отрезок OE параллелен KD и проходит через середину — следовательно, является средней линией и проходит через середину KC. Пункт «а» задания выполнен. Разобраться с пунктом «б» при данном дополнительном построении сложнее. К ответу 3:7 приводит то, что KB с BY соотносятся так же, как ED с YE.

Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

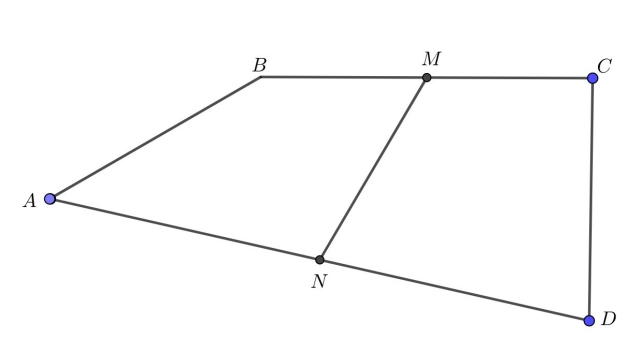
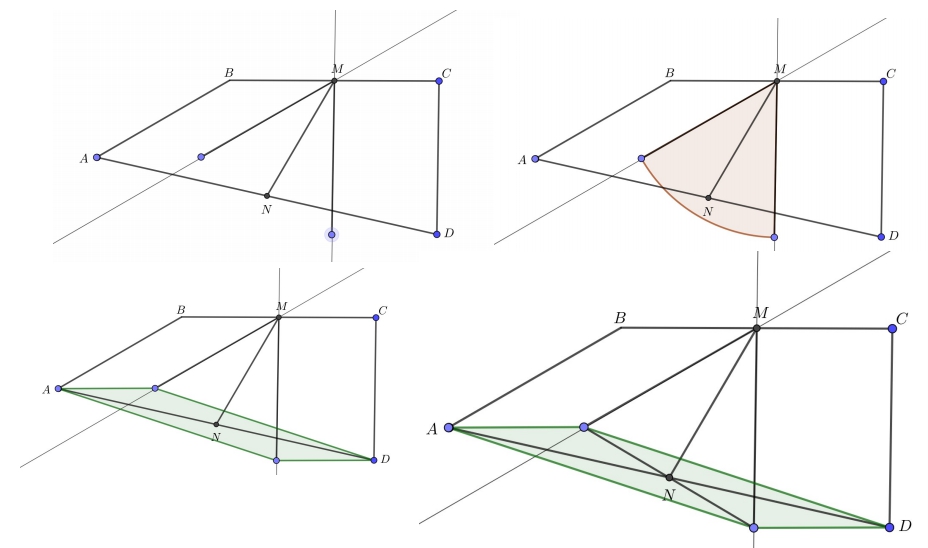
Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Начинаем компоновку данных с точки М и проводим через нее две прямые, параллельные АВ и CD. Далее от точки М откладываем отрезки, равные АВ и, соответственно, CD. Так получается заготовка для равнобедренного треугольника. Нужно понять, будет ли точка N лежать на отрезке, соединяющем две новые точки. Строятся новые отрезки, равные и параллельные ВМ и МС — получается четырехугольник-параллелограмм. AD является диагональю этого параллелограмма, а N — серединой диагонали. Также N лежит и на другой диагонали. Равнобедренный треугольник готов. Угол с вершиной M в нем равен 60°. Треугольник равносторонний, MN является медианой и биссектрисой. MN, пресекаясь с BC, образует угол, равный 60°.

Чтобы ученики прочно запоминали формулы и теоремы, лучше как можно чаще давать им решать подобные задачи. К слову, задачи с трапециями оптимально подходят для отработки навыка дополнительного построения: две параллельные стороны открывают широкие возможности для создания разных геометрических фигур. Об этом – в учебнике «Геометрия. 7-9 классы».

Видео:Три важных дополнительных построения в треугольникеСкачать

исследовательская работа «Решение задач по геометрии методом дополнительных построений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Объект исследования: стереометрические задачи по геометрии

Предмет исследования: геометрия

Цель исследования: выявление способа, позволяющего решать задачи нетрадиционным методом.

Изучить литературу по теме исследования.

Проанализировать способы решения задач и выбрать более эффективный.

Для каждой фигуры найти рациональный метод построения.

Показать практическое применение данного метода.

Подобрать примеры для решения задач предложенным мной методом.

Классификация дополнительных построений……………………4-21

Практическое применение приёма метода дополнительных построений………………………………………………………….22-30

Задачи на доказательство………………………………………….31-32

Задачи на вычисление……………………………………………. 33-35

Список использованной литературы……………………………….37

В геометрии существуют задачи к которым традиционные методы(методы геометрических треугольников, векторный метод, метод равных треугольников) или не применимы, или дают сложные и громоздкие решения. При решении задач такого вида помогает введение в чертёж дополнительных линий или проведение дополнительных построений. В таких задачах это единственный способ её решения. Так как чертёж данной в задаче фигуры можно достроить до фигуры другого типа, то всегда с многоугольной фигурой можно связать окружность и можно на чертеже выделить равные и подобные фигуры.

Суть данного метода дополнительных построений заключается в том, что чертёж и задача, на котором трудно заметить связь между данными и искомыми величинами, дополняется новыми элементами, после чего эти связи становятся очевидными.

Анализ решений задач показал, что для каждой фигуры существуют характерные признаки, которые можно классифицировать. Предлагаю классификацию, которую мне удалось выделить для некоторых фигур.

Классификация дополнительных построений.

Если в треугольнике задана медиана, то его можно достроить до параллелограмма, где основание медианы это точка пересечения диагоналей.

Если в треугольнике создан отрезок, соединяющий вершину с противоположной стороной, то через основание отрезка проводим прямую параллельную стороне треугольника.

М N ‖ АВ или прямую параллельную АС

В результате данного построения получаются подобные треугольники ΔАВС

ΔМ N С или по теореме Фалеса получаются пропорциональные отрезки:

что позволяет определить неизвестные стороны треугольника. Если АМ – медиана Δ АВС, тогда N всегда будет серединой отрезка АС.

Если в треугольнике задана медиана и отрезок, соединяющий вершину с противоположной стороной, то через основание медианы проводим прямую, параллельную данному отрезку.

ДК – средняя линия Δ В N С

3) NK = KC , К – середина NC

Если в треугольнике заданы два отрезка, проведённых из разных вершин, то проводится а) через основание одного отрезка прямая, параллельная другому отрезку

б) прямая, проходящая через вершину треугольника параллельная стороне до пересечения с прямой, содержащей один из отрезков

Если в треугольнике задан отрезок, проведённый из вершины до противоположной стороны и отрезок, соединяющий две другие стороны, но не параллелен его стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит отрезок.

Если в треугольнике задан отрезок с концами на его сторонах и если продолжение этого отрезка пересекает прямую, содержащую третью сторону треугольника, то:

а) продолжаем отрезок до пресечения с прямой, проведённой через вершину треугольника параллельно третьей стороне.

б) проводим прямую, параллельную одной из сторон до пересечения с другой стороной.

а)

б)

Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника, в котором один из катетов данного треугольника становится высотой ( медианой и биссектрисой), а другой – половиной основания.

Если дана трапеция, то её диагональ или боковая сторона переносятся на вектор, определяемый одним из оснований.

Если в треугольнике, параллелограмме или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится ромб, две стороны которого направлены по сторонам данной фигуры, а эта биссектриса является одной из диагоналей.

Если в треугольнике, параллелограмма или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится треугольник, одна из сторон которого содержит эту биссектрису, вторая совпадает со стороной исходной фигуры, а третья либо параллельна другой стороне этой фигуры, либо получается при её продолжении.

Если дана трапеция, то посредством продолжения боковых сторон она достраивается до треугольника.

Если дан четырёхугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность.

Если в треугольнике заданы биссектриса и медиана или биссектриса и серединный перпендикуляр, проведённые к одной и той же стороне, то около треугольника описывается окружность, а биссектриса продолжается до пересечения с нею.

Если даны две окружности разных радиусов с общей касательной, то через центр меньшей окружности проводится прямая, параллельная данной касательной, до пересечения с радиусом большей окружности, идущим в точку касания, или с его продолжением.

Практическое применение метода дополнительных построений.

Две стороны треугольника равны 10см и 15см, угол между ними равен 60 0 . Найти длину биссектрисы, проведённой из данного угла.

проведём MN ‖ АВ

Δ ANM – равнобедренный

AN = x, NC = 15 – x

(15 – х) : 15 = х : 10

По теореме косинусов:

АМ 2 = AN 2 + NM 2 – 2 ∙ AN ∙ NM ∙ cos 120 0

АМ 2 = 36 + 36 – 2 ∙ 36 ∙ cos 120 0

АМ 2 = 72 + 2 ∙ 36 ∙ cos 60 0

АМ 2 = 72 + 36 = 108

В треугольнике АВС высота АМ равна медиане BN . Найти NBC .

проведём NK ‖ AM

AN = NC , AM ‖ NK , тогда по теореме Фалеса МК = КС.

NK – средняя линия Δ АМС,

NK = АМ

Δ BNK – прямоугольный

NK = АМ = = BN

Катет, лежащий против угла в 30 0 равен половине гипотенузы

Доказать, что если диагонали трапеции равны, то она равнобокая.

Дано: А B С D – трапеция

Доказать: АВ = С D

BDA = CMA как соответственные угла при параллельных прямых.

BD = CM , BD = AC , тогда АС = СМ,

Δ АСМ – равнобедренный,

Δ ABD = Δ DCA ( II признак равенства треугольников), тогда AB = CD ,

ABCD – равнобокая трапеция.

Биссектриса острого угла равнобокой трапеции делит боковую сторону на отрезки длиной 20см и 30см, считая от меньшего основания, которое равно 6см. Найти площадь трапеции.

Дано: ABCD – трапеция

BN ‖ AD BN ∩ AN = N

Δ ABN – равнобедренный

накрестлежащие , BN ‖ AD)

CN = BN – BC = 50 – 6 = 44 см

AD : CN = DM : С M

S = ( AD + ВС ) ∙ ВЕ

АЕ = ( AD — ВС) = 30 см

Δ АЕВ – прямоугольный

ВЕ 2 = АВ 2 – АЕ 2

ВЕ 2 = 2500 – 900 = 1600

S = ( 66 + 6 ) ∙ 40 = 1440 см 2

Ответ: 1440 см 2

На стороне АВ треугольника АВС построен равносторонний треугольник АВ D . Найти расстояние от центра этого треугольника до вершины С, если АВ = 5√3, 0 .

Опишем около четырёхугольника ABCD окружность.

D = 180 0 (сумма противолежащих углов)

0 – 180 0 = 180 0

Δ АВС – вписанный в окружность. ОС = R

Ответ: 5 см

Даны две окружности, касающиеся между собой внешним образом в точке С. Прямая а касается обеих окружностей. Найти расстояние от точки С до общей касательной а данных окружностей, если известны их радиусы R ₁ = 10 см, R ₂ = 8см.

а – касательная к окружностям АВ а, MN a , CD a

построим отрезки СВ и С N

Δ ВС N – прямоугольный, BN – гипотенуза, CD – высота, проведённая к гипотенузе

Так как AB ‖ CD ‖ MN , то по теореме Фалеса

BD : DN = 5 : 4, BN = 2√ АВ ∙ MN

Ответ:

Задачи на доказательство.

Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.

На сторонах АВ и ВС треугольника АВС построены вне его квадраты. Доказать, что отрезок, соединяющий вершины квадратов, в два раза больше медианы, проведённой из вершины В.

В треугольнике АВС луч, выходящий из вершины А, делит медиану ВВ₁ в отношении 1: 2. Доказать, что этот луч делит противоположную сторону треугольника в отношении 1: 4.

Доказать, что если в прямоугольном треугольнике один острый угол равен 30 0 , то противолежащий ему катет равен половине гипотенузы.

Катеты прямоугольного треугольника равны a и b . Доказать, что биссектриса прямого угла этого треугольника равна .

Через середину О гипотенузы АВ прямоугольного треугольника АВС проведена прямая, перпендикулярная АВ, и на этой прямой в обе стороны от точки О отложены отрезки О D и ОЕ, равные половине гипотенузы. Доказать, что [ CD ) и [ CE ) – биссектрисы внутреннего и внешнего углов треугольника АВС при вершине С.

Доказать, что прямая, соединяющая основания двух высот остроугольного треугольника, отсекает от него треугольник, подобный данному.

Точка D лежит на стороне АС правильного треугольника АВС, а точка Е – середина отрезка А D . Прямые, перпендикулярные сторонам АВ и ВС данного треугольника и проходящие соответственно через точки D и С, пересекаются в точке F . Доказать, что треугольник ВЕ F прямоугольный с острыми углами 30 0 и 60 0 .

Окружность радиусов R и r ( R > r ) касаются друг друга внешним образом. Доказать, что радиус третьей окружности, касающейся двух данных окружностей и их общей внешней касательной, равен

Две окружности радиусов R и r ( R > r ) касаются друг друга и сторон данного угла. Доказать, что радиус третьей окружности, касающейся сторон того же угла, центр которой находится в точке касания между собой двух данных окружностей, равен