В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные прямой а1в1

Вопрос по геометрии:

В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые параллельные прямой B1C1

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

В кубе в плоскости ABCD B1C1||BC||AD

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные прямой а1в1

БАЗА ЗАДАНИЙ

Задание № 13. Стереометрия с доказательством.

1. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите угол наклона плоскости α к плоскости грани BB ₁ C ₁ C.

2. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

4. В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2

5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3

7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Ответ: б) 2,4

8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.

9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9. Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
а) Докажите, что плоскость CEF параллельна ребру SB.

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

10. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона основания AB равна 6, а боковое ребро AA ₁ равно 2√2. На рёбрах AB, A ₁ B ₁ и B ₁ C ₁ отмечены точки M, N и K соответственно, причём AM = B ₁ N= C ₁ K=2.
а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Ответ: б) 15

11. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 6, а боковое ребро AA ₁ =3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A ₁ C ₁ и B ₁ C ₁ соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4

12. В правильной четырёхугольной призме ABCDA ₁ B ₁ C ₁ D ₁ сторона AB основания равна 8, а боковое ребро AA ₁ равно 4√2. На рёбрах BC и C ₁ D ₁ отмечены точки K и L соответственно, причём BK= C ₁ L=2. Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A ₁ C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.

13. В основании прямой треугольной призмы ABCA ₁ B ₁ C ₁ лежит равнобедренный (AB=BC) треугольник ABC. Точка K— середина ребра A ₁ B ₁ , а точка M делит ребро AC в отношении AM:MC=1:3.
а) Докажите, что KM⊥AC.
б) Найдите угол между прямой KM и плоскостью ABB ₁ , если AB=6, AC=8, AA ₁ = 3.

14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB=2√2, AD=6, AA₁=10. На рёбрах AA₁ и BB₁ отмечены точки E и F соответств., причём A ₁ E:EA =3:2 и B ₁ F:FB=3:7. Точка T — середина ребра B ₁ C ₁ .
а) Докажите, что плоскость EFT проходит через точку D ₁ .
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Ответ: б) 22,5

а) Докажите, что плоскость EFT проходит через вершину D₁.

б) Найдите угол между плоскостью EFT и плоскостью AA₁B₁.

16. На ребрах CD и BB1 куба ABCDA₁B₁C₁D₁ c ребром 12 отмечены точки Р и Q соответственно, причем DP=4, а B ₁ Q=3. Плоскость APQ пересекает ребро CC ₁ в точке М.
а) Докажите, что точка М является серединой ребра CC ₁ .
б) Найдите расстояние от точки С до плоскости APQ.

17. В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM=DN=4 и АК=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.

18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.

19. Основанием прямой четырехугольной призмы ABCDA ₁ B ₁ C ₁ D ₁ является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA ₁ в соотношении AK:KA ₁ =1:2. Через точки K и B проведена плоскость α, параллельная прямой AC и пересекающая ребро DD ₁ в точке M.
а) Докажите, что плоскость α делит ребро DD ₁ в отношении DM:MD ₁ =2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6

20. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 12, а боковое ребро AA ₁ равно 3√6. На ребрах AB и B ₁ C ₁ отмечены точки K и L соответственно, причем AK=2, B ₁ L=4. Точка M середина A ₁ C ₁ . Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2

21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 и BC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30

22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=AQ=RC=2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2

23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90

24. Основанием прямой треугольной призмы ABCA ₁ B ₁ C ₁ является прямоугольный треугольник ABC с прямым углом C. Прямые CA ₁ и AB ₁ перпендикулярны.
а) Докажите, что AA ₁ =AC.
б) Найдите расстояние между прямыми CA ₁ и AB ₁ , если AC = 6, BC = 3.
Ответ: б) √2

6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

3. Сечением прямоугольного параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ плоскостью α, содержащей прямую BD ₁ и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.
б) Найдите угол между плоскостями α и BCC ₁ , если AA ₁ =10, AB=12.

База заданий сформирована из Официального Банка заданий ФИПИ,

Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные прямой а1в1

Контрольная работа по геометрии в 10 классе «Параллельные плоскости. Тетраэдр. Параллелепипед» с ответами и решениями (легкий уровень). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 10 класса. Урок 23. Геометрия 10 класс Контрольная № 2 «Параллельные плоскости. Тетраэдр. Параллелепипед» Уровень 1.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Контрольная работа № 2

Уровень 1 (легкий). Геометрия 10 класс

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

Вариант 1

1. Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А₁ и В₁. Найдите А₁В₁, если АВ = 5 см.
2. Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
3. Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А₁ и A₂, В₁ и В₂. Известно, что МА₁ = 4 см, В₁В₂ = 9 см, A₁A₂ = МВ₁. Найдите МА₂ и MB₂.

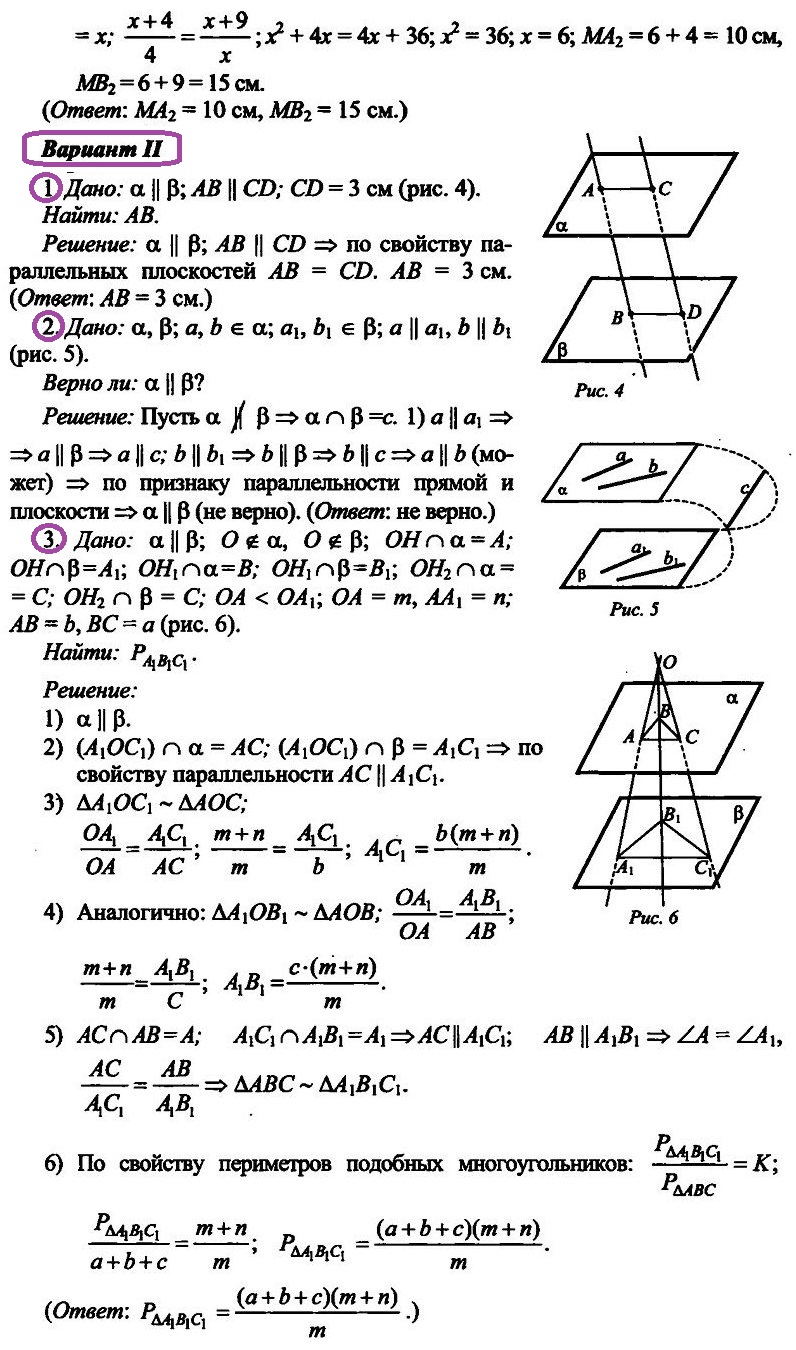
Вариант 2

1. Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см.
2. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?
3. Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А₁, В₁, С₁ (ОА ОТВЕТЫ на контрольную работу:

Смотрите также задания и ответы на контрольную работу № 2 для других уровней:

Вы смотрели: Геометрия 10 класс Контрольная № 2 (легкий уровень). Поурочное планирование по геометрии для 10 класса. УМК Атанасян (Просвещение). Урок 23. Контрольная работа по геометрии «Параллельные плоскости. Тетраэдр. Параллелепипед» + ОТВЕТЫ.

(с) В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 10 класс — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

🌟 Видео

№19. Стороны АВ и ВС параллелограмма ABCD пересекают плоскость αСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Геометрия Диагонали грани ABCD куба ABCDA1B1C1D1 пересекаются в точке O Найдите угол между прямымиСкачать

№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Параллельность прямых. 10 класс.Скачать

№154. Прямая BD перпендикулярна к плоскости треугольника ABC. Известно, что BD = 9 смСкачать

№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

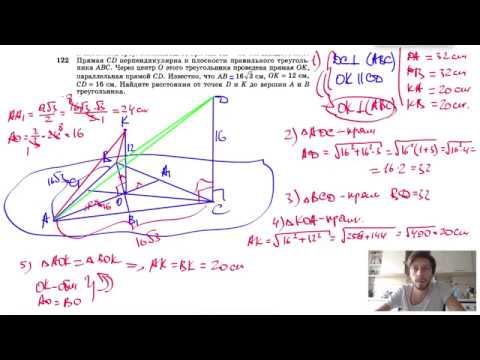
№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать