Дайте определение параллельных пересекающихся и скрещивающихся прямых

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

1. признаки скрещивающихся прямых;
2. определение углов с сонаправленными сторонами;
3. доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых;
4. доказательство теоремы о равенстве углов с сонаправленными сторонами.

Глоссарий по теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

1. Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл.– М.: Просвещение, 2014.

1. Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
2. Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

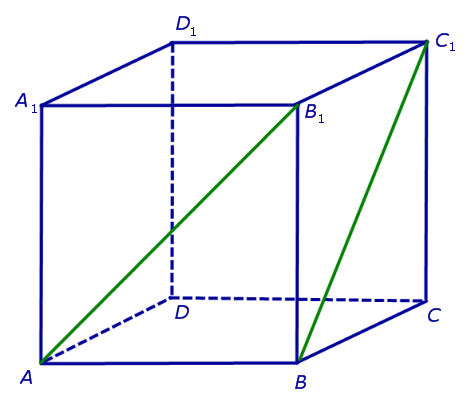
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

1. Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
   2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
   3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
   Теорема доказана.

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

1. Стороны углов сонаправлены, а, значит, параллельны. Проведем через них плоскости- как показано на чертеже.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Видеоурок: Параллельные прямые, перпендикулярные к плоскости

Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Пересекающиеся прямые

Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.

Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.

Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.

Параллельность

Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.

Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.

Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.

Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.

При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.

Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.

Перпендикулярность

Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.

В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.

Скрещенные прямые. Секущая

У любых скрещивающихся прямых есть вертикальные углы и смежные.

Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:

Смежные углы в сумме дают 180 градусов.

Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:

Вертикальные углы всегда равны.

Если же некоторая прямая пересекает две других прямых, то она называется секущей.

Частным случаем является секущая двух параллельных прямых:

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми

параллельно

пересекаются

скрещиваются

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		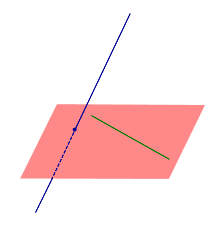Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		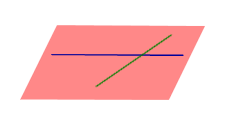Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		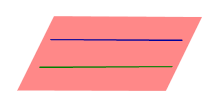Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

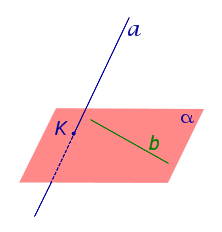
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

Угол между скрещивающимися прямыми

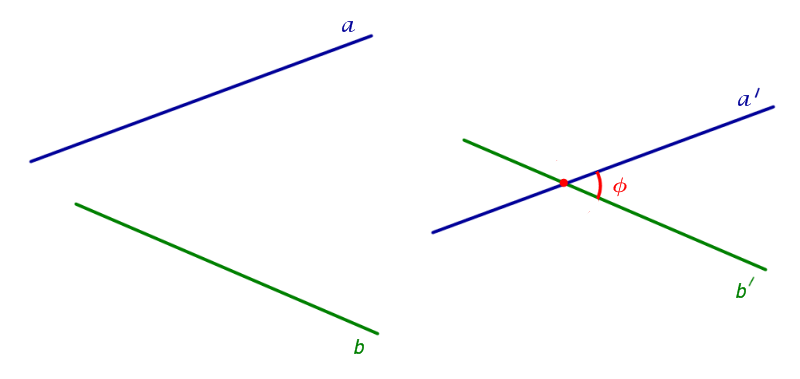
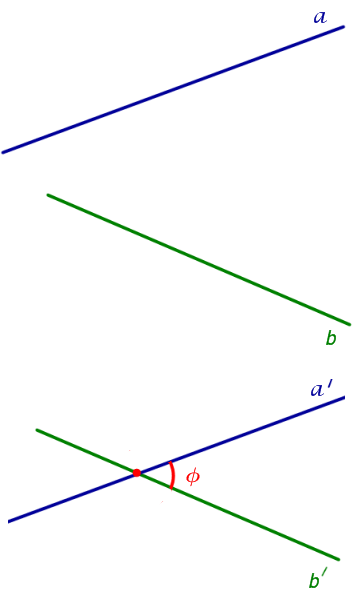
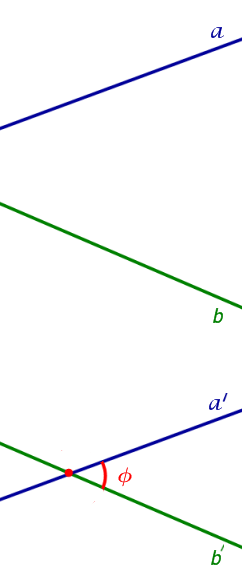
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

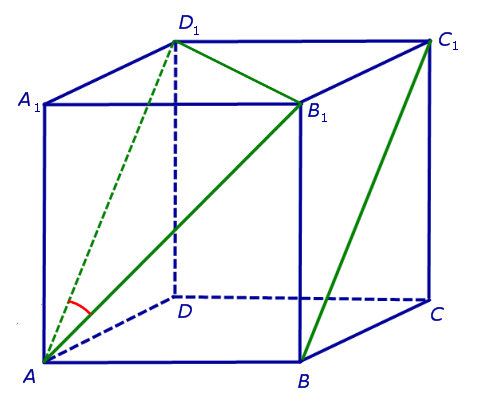
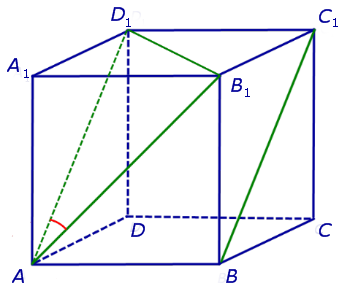
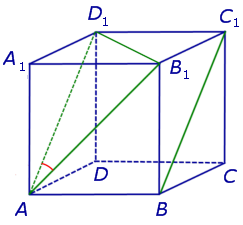
Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

📹 Видео