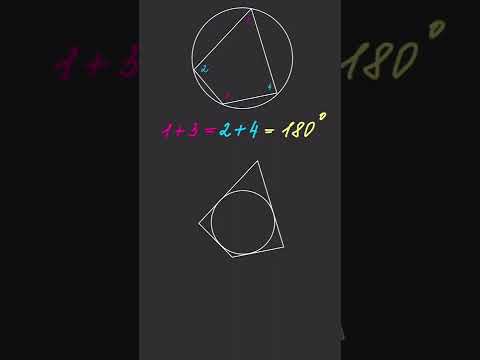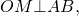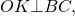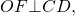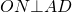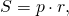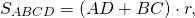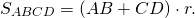Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Проверим каждое из утверждений.
1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны» — верно, по признаку параллельности прямых.
2) «В любой четырёхугольник можно вписать окружность» — неверно, поскольку в выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
3) «Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника» — верно, по свойству треугольника.
Вписанная в четырехугольник окружность
Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.
Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
В четырехугольник ABCD можно вписать окружность, если
И обратно, если суммы противоположных сторон четырехугольника равны:
то в четырехугольник ABCD можно вписать окружность.
Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.
O — точка пересечения биссектрис четырехугольника ABCD.
AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,
то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.
3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.
AM=AN,
5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
где p — полупериметр четырехугольника.
Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.
Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и
Соответственно, радиус вписанной в четырехугольник окружности равен
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны
Пусть окружность вписана в четырехугольник АВСD. Докажем, что суммы длин противоположных сторон четырехугольника равны.
Отрезки касательных, проведенных к окружности из точек А, В, С и D, обозначим соответственно а, b, с и d.
Тогда АВ + СD = АD + ВС = а + c = b + d.
Докажем обратное утверждение.
Формулируется оно так: Если суммы длин противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Пусть в четырехугольнике АВСD равны суммы длин противоположных сторон: АВ + СD = АD + ВС. Докажем, что в четырехугольник АВСD можно вписать окружность.
Проведем AO и BO – биссектрисы углов A и B, AO ∩ BO = O.
Точка O равноудалена от сторон AB, BC и AD четырёхугольника АВСD. Окружность с центром О касается сторон АВ, ВС и AD четырехугольника.
Покажем, что окружность с центром в точке O касается также стороны CD, то есть вписана в четырёхугольник ABCD.
Предположим, что это не так, и CD либо не имеет общих точек с окружностью, либо является секущей.
Рассмотрим первый случай. Проведем касательную параллельно CD. Четырехугольник – описанный вокруг окружности, и для него выполняется равенство:
.
При этом . Получим:
С другой стороны,
поэтому
и .
Получили, что для четырехугольника длина стороны CD равна сумме трех других сторон. Это невозможно. Мы пришли к противоречию. Предположение о том, что CD не имеет общих точек с окружностью, было неверно.
Аналогично доказывается, что CD не может быть секущей к окружности. Значит, CD – касательная к окружности и четырехугольник ABCD – описанный вокруг окружности.
Задача ЕГЭ по теме «Описанный четырехугольник»
В четырёхугольник ABCD вписана окружность, AB=10, CD=16. Найдите периметр четырёхугольника ABCD.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,
Тогда периметр четырехугольника равен .