В равнобедренную трапецию ABCD с основаниями BC и AD вписана окружность. Вторая окружность, построенная на боковой стороне AB как на диаметре, второй раз пересекает большее основание AD в точке H.
а) Докажите, что треугольник CHD равнобедренный.
б) Найдите основания трапеции, если радиусы первой и второй окружностей равны соответственно 6 и 6,5.
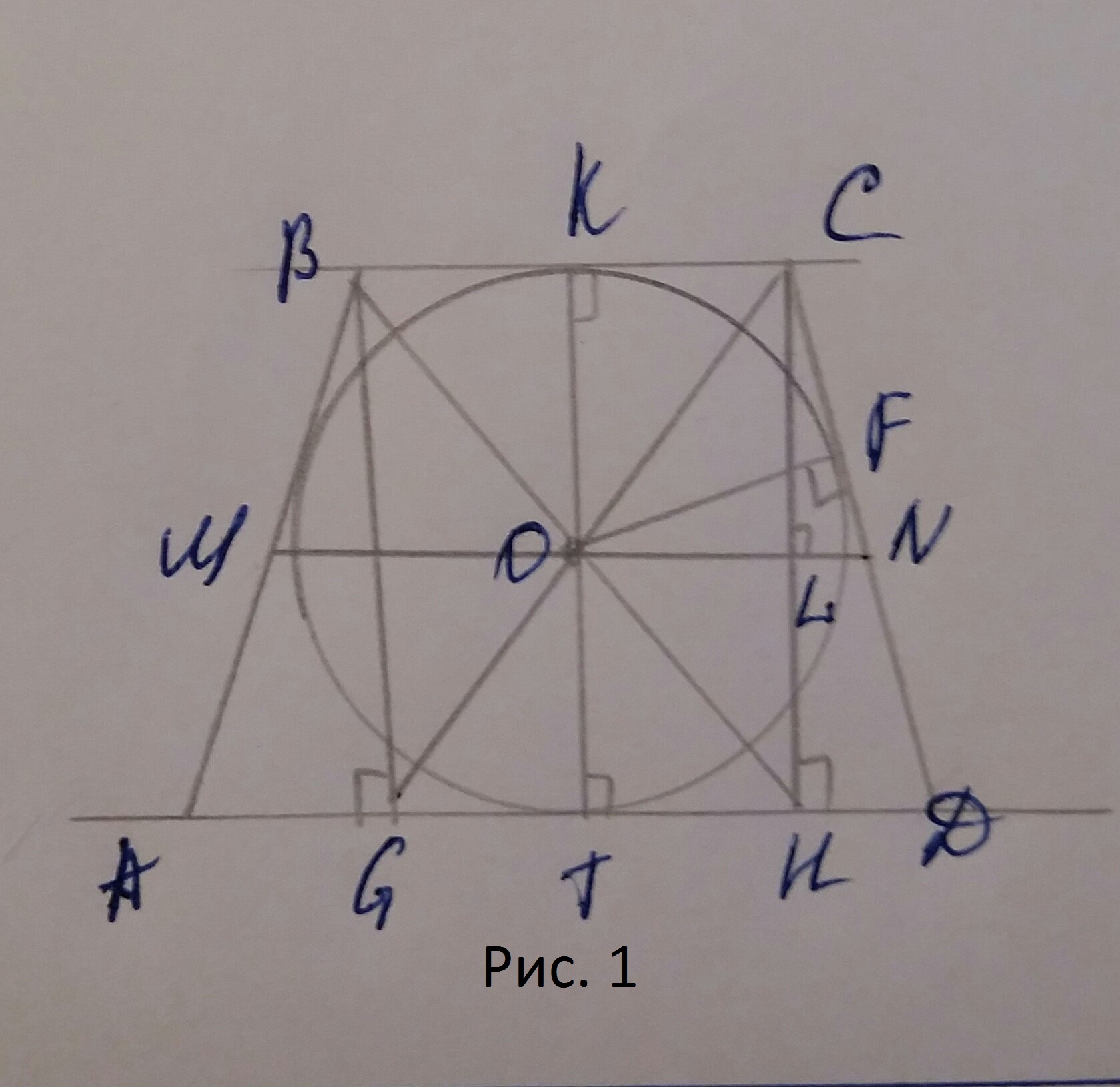
а) Доплнительные построения и обозначения:
О — центр вписанной окружности; O1 — середина отрезка AB; MN — отрезок, соединяющий середины оснований равнобедренной трапеции; ОМ, ОN радиусы вписанной окружности; E — проекции С на АD; K — точка касания первой окружности стороны трапеции CD.
Рассмотрим Δ OMC и Δ ONH. Они прямоугольные, у них: ОМ = ОN как радиусы одной и той же окружности, ∠MOC = ∠NOH как вертикальные. Значит, Δ OMC = Δ ONH, откуда MC = NH.
Имеем: D = KC + KD, DH = DN + NH. По свойству касательных, проведенных к окружности из одной и той же точки: DN = KD. Прибавим к левой и правой частям этого равенства равные отрезки NH и МС соответственно. Получим верное равенство: DN + NH = KD + MC. В правой части слагаемое МС заменим равным KC. Тогда будем иметь: DN + NH = KD + KC, а это значит, что DH = DC, что и требовалось доказать.
б) В четырехугольник можно вписать окружность только в том случае, если суммы противоположных сторон четырехугольника равны. Следовательно, 2AB = AD + BC, т. е. AD + BC = 2 · 2 · 6,5 = 26.
BH ⊥ AD, так как ∠ AHB = 90° как вписанный угол, опирающийся на диаметр второй окружности. CE ⊥ AD по построению, значит, BH||CE. Кроме того, BC||AD по определению трапеции, следовательно, HBCE — прямоугольник, BC = HE, BH = CE.
В прямоугольном треугольнике AHB
Значит, откуда
| Критерии оценивания выполнения задания | Баллы | |
|---|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 | |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 | |
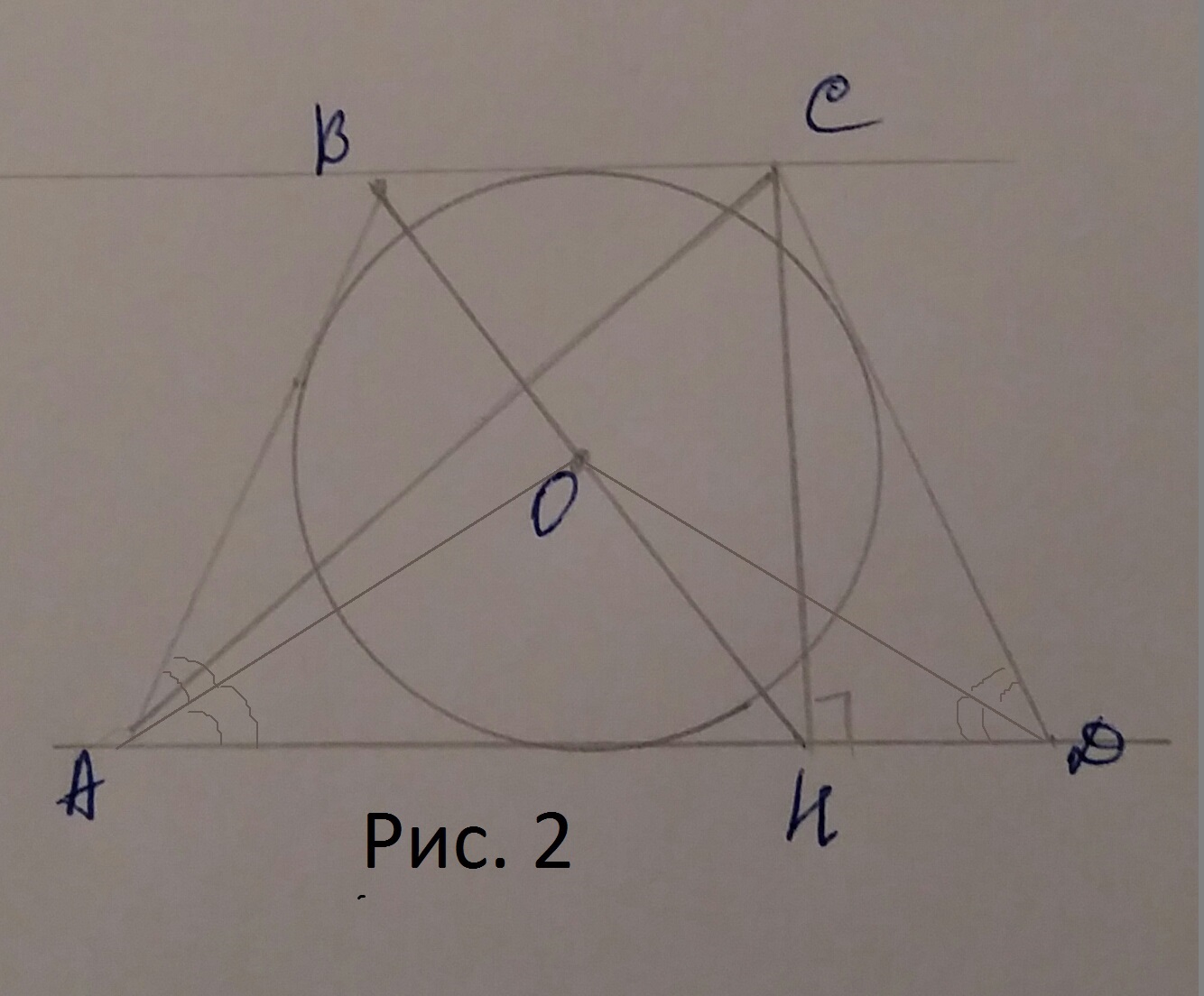
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание Видео:Задача про трапецию, описанную около окружностиСкачать  Задача 8190 В равнобедренную трапецию ABCD с.УсловиеВ равнобедренную трапецию ABCD с основаниями AD и BC вписана окружность, CH — высота трапеции. а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке BH. б) Найдите диагональ AC, если известно, что средняя линия трапеции равна 2sqrt(7), а угол AOD=120 градусов, где O — центр окружности, вписанной в трапецию, а AD — большее основание. Решениеа)См. рис. 1 б)См. рис. 2 Видео:Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать  Задача 4 (описанный четырехугольник).В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции. а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.
б) Найдите диагональ АС, если известно, что средняя линия трапеции равна а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда 2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу (углы OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН. 3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу) 4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан. б) Для доказательства пункта б) сделаем дополнительный чертеж 1) Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО = 2) АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО= 3) ∠AOD=135° (по условию), ∠OAD+∠ODA=45°. Значит, ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD. BR = AR= 4) Пусть CD1 II BD и точка D1 лежит на прямой AD. Четырехугольник ВСD1D – параллелограмм. CD1=BD (противоположные стороны), BD=AC(диагонали равнобедренной трапеции). Тогда СD1=BD=AC. 5) Задача 5 В треугольнике АВС угол ВАС равен 60 ° , угол АВС равен 45 ° . Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P. а) Докажите, что треугольник MNP прямоугольный. б) Найдите площадь треугольника MNP, если ВС=12. Повторить. Свойство вписанных углов; теорему синусов. Тогда вписанные углы PNB и PCB опираются на одну и ту же дугу, поэтому Аналогично, Следовательно, треугольник MNP прямоугольный. Пункт а) доказан. б) Угол MNA равен углу NBA , угол APM равен углу ACP (вписанные углы, опирающиеся на одну дугу). Тогда Следовательно, Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов Тогда Следовательно, 📽️ ВидеоОГЭ по математике. Задание 15Скачать  ОГЭ 2022 Математика Задача №23 Вариант 4 Сборник под редакцией Ященко 36 вариантов.Скачать 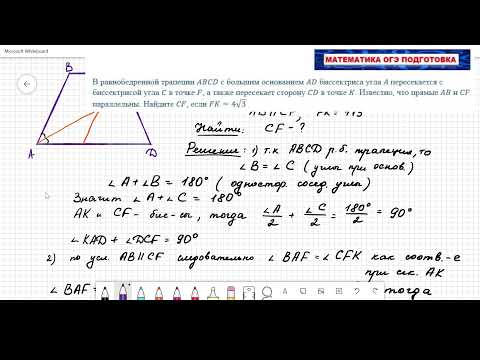 №387. Найдите углы В и D трапеции ABCD с основаниями AD и ВС, если ∠A=36°, ∠C= 117°.Скачать  4.43.1. Планиметрия. Гордин Р.К.Скачать  Трапеция. Практическая часть - решение задачи. 8 класс.Скачать  16 ЗАДАНИЕ ОГЭ ИЩЕМ УГОЛ А В ТРАПЕЦИИ ИЗ КРУГАСкачать  Окружность вписана в равнобедренную трапецию. Теорема в задаче. Геометрия, ОГЭ, ЕГЭ. Высота и радиусСкачать  ОГЭ 2020 задание 18Скачать  8 класс, 6 урок, ТрапецияСкачать  Геометрия. ОГЭ по математике. Задание 17Скачать  Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать  Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать  Задание второй части реального варианта ЕГЭ 2015 Планиметрия #3Скачать  Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать  ЕГЭ 2022 16 вариант 3 задача.Скачать  Задание 26 Равнобедренная трапеция Окружности, вписанные в треугольникиСкачать  17)Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 61°.Найдите угол C этойСкачать  Задание 26 Равнобедренная трапеция, описанная и вписанная окружностиСкачать  |
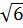 , а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.
, а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.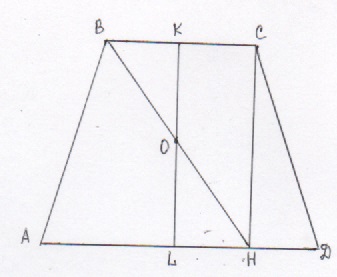
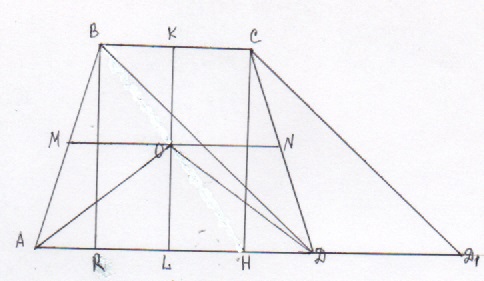
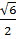
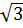
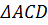 1 – равнобедренный, AD1 – основание. АD1=AD+DD1=AD+BC=2MN=2
1 – равнобедренный, AD1 – основание. АD1=AD+DD1=AD+BC=2MN=2 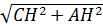 =
= 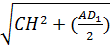 2 =
2 = 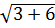 = 3
= 3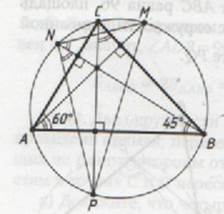 а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.
а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.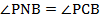
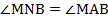
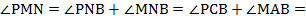
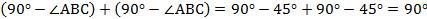
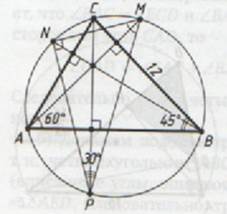
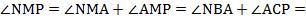
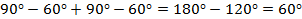
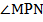 = 30 ° .
= 30 ° .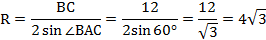
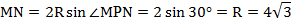
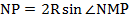 =
= 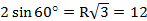
 Ответ:
Ответ: